Article contents
CONFORMALLY FLAT CONTACT THREE-MANIFOLDS
Published online by Cambridge University Press: 03 November 2016
Abstract
In this paper, we consider contact metric three-manifolds 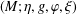 $(M;\unicode[STIX]{x1D702},g,\unicode[STIX]{x1D711},\unicode[STIX]{x1D709})$ which satisfy the condition
$(M;\unicode[STIX]{x1D702},g,\unicode[STIX]{x1D711},\unicode[STIX]{x1D709})$ which satisfy the condition 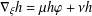 $\unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D709}}h=\unicode[STIX]{x1D707}h\unicode[STIX]{x1D711}+\unicode[STIX]{x1D708}h$ for some smooth functions
$\unicode[STIX]{x1D6FB}_{\unicode[STIX]{x1D709}}h=\unicode[STIX]{x1D707}h\unicode[STIX]{x1D711}+\unicode[STIX]{x1D708}h$ for some smooth functions 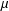 $\unicode[STIX]{x1D707}$ and
$\unicode[STIX]{x1D707}$ and  $\unicode[STIX]{x1D708}$, where
$\unicode[STIX]{x1D708}$, where 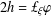 $2h=\unicode[STIX]{x00A3}_{\unicode[STIX]{x1D709}}\unicode[STIX]{x1D711}$. We prove that if
$2h=\unicode[STIX]{x00A3}_{\unicode[STIX]{x1D709}}\unicode[STIX]{x1D711}$. We prove that if 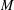 $M$ is conformally flat and if
$M$ is conformally flat and if 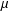 $\unicode[STIX]{x1D707}$ is constant, then
$\unicode[STIX]{x1D707}$ is constant, then 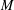 $M$ is either a flat manifold or a Sasakian manifold of constant curvature
$M$ is either a flat manifold or a Sasakian manifold of constant curvature 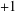 $+1$. We cannot extend this result for a smooth function
$+1$. We cannot extend this result for a smooth function 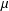 $\unicode[STIX]{x1D707}$. Indeed, we give such an example of a conformally flat contact three-manifold which is not of constant curvature.
$\unicode[STIX]{x1D707}$. Indeed, we give such an example of a conformally flat contact three-manifold which is not of constant curvature.
MSC classification
- Type
- Research Article
- Information
- Journal of the Australian Mathematical Society , Volume 103 , Issue 2 , October 2017 , pp. 177 - 189
- Copyright
- © 2016 Australian Mathematical Publishing Association Inc.
Footnotes
This research was supported by Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education, Science and Technology (2014R1A1A2053665).
References
- 2
- Cited by


