Article contents
CHAIN CONDITIONS ON ÉTALE GROUPOID ALGEBRAS WITH APPLICATIONS TO LEAVITT PATH ALGEBRAS AND INVERSE SEMIGROUP ALGEBRAS
Published online by Cambridge University Press: 28 March 2018
Abstract
The author has previously associated to each commutative ring with unit 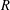 $R$ and étale groupoid
$R$ and étale groupoid 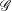 $\mathscr{G}$ with locally compact, Hausdorff and totally disconnected unit space an
$\mathscr{G}$ with locally compact, Hausdorff and totally disconnected unit space an 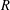 $R$-algebra
$R$-algebra 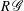 $R\,\mathscr{G}$. In this paper we characterize when
$R\,\mathscr{G}$. In this paper we characterize when  $R\,\mathscr{G}$ is Noetherian and when it is Artinian. As corollaries, we extend the characterization of Abrams, Aranda Pino and Siles Molina of finite-dimensional and of Noetherian Leavitt path algebras over a field to arbitrary commutative coefficient rings and we recover the characterization of Okniński of Noetherian inverse semigroup algebras and of Zelmanov of Artinian inverse semigroup algebras.
$R\,\mathscr{G}$ is Noetherian and when it is Artinian. As corollaries, we extend the characterization of Abrams, Aranda Pino and Siles Molina of finite-dimensional and of Noetherian Leavitt path algebras over a field to arbitrary commutative coefficient rings and we recover the characterization of Okniński of Noetherian inverse semigroup algebras and of Zelmanov of Artinian inverse semigroup algebras.
Keywords
- Type
- Research Article
- Information
- Copyright
- © 2018 Australian Mathematical Publishing Association Inc.
References
- 10
- Cited by


