Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-27T01:24:31.329Z Has data issue: false hasContentIssue false
  • English
  • Français

Altitudes of a simplex in n-space

Published online by Cambridge University Press:  09 April 2009

Sahib Ram Mandan
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In continuation of the two previous papers (10; 11), this paper was originally written at the Indian Institute of Technology, Kharagpur and revised at the University of Sydney under the advice of Prof. T. G. Room. Although the altitudes of a general simplex S(A) in n-space (n > 2) do not concur as they do for a triangle (n = 2), yet we observe that its Monge point, M (1; 5), is an appropriate analogue of the orthocentre of a triangle such that M coincides with its orthocentre when it is orthogonal (or orthocentric). In consistency with the previous papers (10; 11; 13; 15) we shall call M as the S-point of S(A) and denote it as S as explained in § 1.2. The altitudes of S(A) are all met by the (n − 2)-spaces normal to its plane faces at their orthocentres, each parallel to 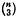of them, thus indicating the associated character of the altitudes as discussed separately in 2 other papers (12; 16). Before we introduce an orthogonal simplex and develop its properties in regard to its γ-altitudes and associated hyperspheres, we come across a number of intermediate ones of special interest. Two special types are treated here and the other two are developed in 2 other papers (13; 15).

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 2 , Issue 4 , December 1962 , pp. 403 - 424
Copyright
Copyright © Australian Mathematical Society 1962

References

[1]Court, N. A., Modern pure solid geometry (New York, 1935).Google Scholar
[2]Court, N. A., On the theory of the tetrahedron, Bul. Amer. Math. Soc. 48 (1942), 583–589.CrossRefGoogle Scholar
[3]Court, N. A., The semi-orthocentric tetrahedron, Amer. Math. Mon. 60 (1953), 306–310.CrossRefGoogle Scholar
[4]Coxeter, H. S. M., Editorial note to solution of problem 3963, Amer. Math. Mon. 49 (1942), 133.Google Scholar
[5]Coxeter, H. S. M., Editorial note to solution of problem 4049, Amer. Math. Mon. 50 (1943), 567–578.Google Scholar
[6]Coxeter, H. S. M., Regular polytopes (London, 1948).Google Scholar
[7]Mandan, S. R., Umbilical projection in four dimensional space S4, Proc. Ind. Acad. Sc. A28 (1948), 166–172.CrossRefGoogle Scholar
[8]Mandan, S. R., Spheres associated with a semi-orthocentric tetrahedron, Res. Bul. Panj. Uni. 127 (1957), 447–451.Google Scholar
[9]Mandan, S. R., An S-configuration in Euclidean and elliptic n-space, Can. J. Math. 10 (1958), 489–501.Google Scholar
[10]Mandan, S. R., Altitudes of a simplex in four dimensional space, Bul. Cal. Math. Soc. 50 (1958 Supp.), 8–20.Google Scholar
[11]Mandan, S. R., Semi-orthocentric and Orthogonal simplexes in a 4-space, Bul. Cal. Math. Soc., 21–29.Google Scholar
[12]Mandan, S. R., Altitudes of a general 4-simplex, Bul. Cal. Math. Soc., 34–41.Google Scholar
[13]Mandan, S. R., Uni-and Demi-orthocentric simplexes, Jour. Ind. Math. Soc. 23 (1959), 169–184.Google Scholar
[14]Mandan, S. R., Medial simplex, Math. St. 28 (1960), 49–52.Google Scholar
[15]Mandan, S. R., Uni- and Demi-orthocentric simplexes II, Journ. Ind. Math. Soc. 25 (1961).Google Scholar
[16]Mandan, S. R., Altitudes of a general n-simplex, Jour. Australian Math. Soc. (in press).Google Scholar
[17]Mandan, S. R., Polarity for a simplex, Jour. Australian Math. Soc.Google Scholar