Hostname: page-component-7479d7b7d-qlrfm Total loading time: 0 Render date: 2024-07-12T07:04:01.530Z Has data issue: false hasContentIssue false
  • English
  • Français

0-dimensional compactifications and Boolean rings

Published online by Cambridge University Press:  09 April 2009

K. D. Magill Jr  and
J. A. Glasenapp
K. D. Magill Jr
Affiliation:
State University of New York at Buffalo
J. A. Glasenapp
Affiliation:
Rochester Institute of Technology
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A subset of a topological space which is both closed and open is referred to as a clopen subset. Here, a 0-dimensional space is a Hausdorff space which has a basis of clopen sets. Here, a 0-dimensional space is a Hausdorff space which has a basis of clopen sets. By a compactification αX of a completely regular Hausdorff space X, we mean any compact space which contains X as a dense subspace. Two compactifications αX and γX are regarded as being equivalent if there exists a homeomorphism from αX onto γX which keeps X pointwise fixed. We will not distinguish between equivalent compactifications. With this convention, we can partially order any family of compactifications of X by defining αX ≧ γX if there exists a continuous mapping from γX onto αX which leaves X pointwise fixed. This paper is concerned with the study of the partially ordered family 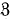[X] of all 0-dimensional compactifications of a 0-dimensional space X.

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 8 , Issue 4 , November 1968 , pp. 755 - 765
Copyright
Copyright © Australian Mathematical Society 1968

References

[1]Boboc, N. and Siretchi, Gh., ‘Sur la compactification d'un espace topologique’, Bull. Math. Sci. Math. Phys. R. P. Roumaine (N.S.) 5 (53) (1961), 155–165 (1964).Google Scholar
[2]Gillman, L. and Jerison, M., Rings of continuous functions (D. Van Nostrand, New York, 1960).CrossRefGoogle Scholar
[3]Lubben, R. G., ‘Concerning the decomposition and amalgamation of points, upper semi-continuous collections and topological extensions’, Trans. Amer. Math. Soc. 49 (1961), 410–466CrossRefGoogle Scholar
[4]Magill, K. D. Jr, ‘ A note on compactifications’, Math. Zeit. 94 (1966), 322–325.CrossRefGoogle Scholar
[5]Sierpinski, W., Introduction to general topology (The University of Toronto Press, 1934).Google Scholar
[6]Visliseni, J. and Flaksmaier, J., ‘The power and structure of the lattice of all compact extensions of a completely regular space’, Doklady 165, (1965), 1423–1425.Google Scholar