Research Article
Redundancies in the Hilbert-Bernays derivability conditions for Gödel's second incompleteness theorem1
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 359-367
-
- Article
- Export citation
Noninitial segments of the α-degrees1
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 368-388
-
- Article
- Export citation
An axiomatisation of quantum logic
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 389-392
-
- Article
- Export citation
Degrees of continuous functionals
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 393-395
-
- Article
- Export citation
On the possibility of a Σ21 well-ordering of the Baire space
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 396-398
-
- Article
- Export citation
Weak definability in infinitary languages
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 399-404
-
- Article
- Export citation
Borel sets and hyperdegrees1
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 405-409
-
- Article
- Export citation
On an Ackermann-type set theory
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 410-412
-
- Article
- Export citation
Complete types and the natural numbers
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 413-415
-
- Article
- Export citation
Limitations on the Fraenkel-Mostowski method of independence proofs
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 416-422
-
- Article
- Export citation
Rowbottom cardinals and Jonsson cardinals are almost the same1
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 423-427
-
- Article
- Export citation
The word problem for division rings
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 428-436
-
- Article
- Export citation
Encodability of Kleene's O
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 437-440
-
- Article
- Export citation
A characterization of terms of the λI-calculus having a normal form
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 441-445
-
- Article
- Export citation
Post's problem and his hypersimple set1
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 446-452
-
- Article
- Export citation
The faithfulness of the interpretation of arithmetic in the theory of constructions
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 453-459
-
- Article
- Export citation
Uncountable models and infinitary elementary extensions
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 460-470
-
- Article
- Export citation
The decision problem for formulas with a small number of atomic subformulas
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 471-480
-
- Article
- Export citation
The characterization of monadic logic
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 481-488
-
- Article
- Export citation
The consistency of a system of combinatory restricted generality*
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 489-492
-
- Article
- Export citation



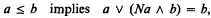
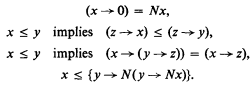
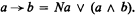
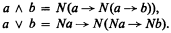
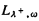 by adding a suitable predicate in more than
by adding a suitable predicate in more than 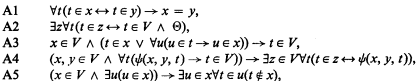
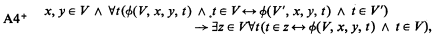
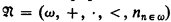 , or in any expansion
, or in any expansion 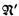 of
of 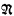 having only countably many relations and operations, there is a proper elementary extension
having only countably many relations and operations, there is a proper elementary extension 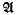 of
of 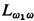 -sentences. The result holds also for countable families of types.
-sentences. The result holds also for countable families of types.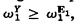 the first recursively inaccessible ordinal. This is accomplished by proving that
the first recursively inaccessible ordinal. This is accomplished by proving that 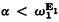
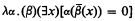
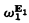 be the smallest ordinal which is not the order type of any well-ordering recursive in
be the smallest ordinal which is not the order type of any well-ordering recursive in 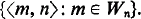 In his quest for nonrecursive incomplete r.e. sets Post [4] constructed a hypersimple set
In his quest for nonrecursive incomplete r.e. sets Post [4] constructed a hypersimple set 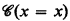 is the set of
is the set of 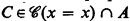 , ⋀Φ → C is not valid
, ⋀Φ → C is not valid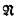 up to
up to 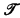 has a nonempty universe ∣
has a nonempty universe ∣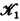 and
and 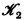 are
are 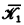 and
and 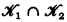 are
are 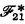 , proposed without a claim as to its consistency in [CLg, §15C], has turned out to entail a consequence which is extremely suspicious. For from the axiom ⊦LH it follows that
, proposed without a claim as to its consistency in [CLg, §15C], has turned out to entail a consequence which is extremely suspicious. For from the axiom ⊦LH it follows that

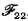 , is demonstrably consistent and sufficient for all practical purposes served by
, is demonstrably consistent and sufficient for all practical purposes served by