Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-27T03:43:41.611Z Has data issue: false hasContentIssue false
  • English
  • Français

Weak systems of determinacy and arithmetical quasi-inductive definitions

Published online by Cambridge University Press:  12 March 2014

P. D. Welch
P. D. Welch*
Affiliation:
School of Mathematics, University of Bristol, Bristol, BS8 1TW, UK, E-mail: p.welch@bristol.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

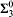We locate winning strategies for various -games in the L-hierarchy in order to prove the following:

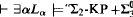Theorem 1. KP + Σ2-Comprehension -Determinacy.”

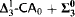Alternatively: “there is a β-model of-Determinacy.” The implication is not reversible. (The antecedent here may be replaced with 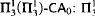instances of Comprehension with only 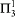-lightface definable parameters—or even weaker theories.)

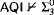Theorem 2. KP + Δ2-Comprehension + Σ2-Replacement + -Determinacy.

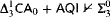(Here AQI is the assertion that every arithmetical quasi-inductive definition converges.) Alternatively: -Determinacy.

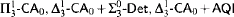Hence the theories: , and 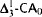are in strictly descending order of strength.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 76 , Issue 2 , June 2011 , pp. 418 - 436
Copyright
Copyright © Association for Symbolic Logic 2011

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Barwise, K. J., Admissible sets and structures, Perspectives in Mathematical Logic, Springer, 1975.CrossRefGoogle Scholar
[2]Burgess, J. P., The truth is never simple, this Journal, vol. 51 (1986), no. 3, pp. 663–681.Google Scholar
[3]Davis, M., Infinite games of perfect information, Annals of Mathematical Studies, vol. 52 (1964), pp. 85–101.Google Scholar
[4]Devlin, K., Constructibility, Perspectives in Mathematical Logic, Springer, 1984.CrossRefGoogle Scholar
[5]Field, H., A revenge-immune solution to the semantic paradoxes, Journal of Philosophical Logic, vol. 32 (2003), no. 3, pp. 139–177.CrossRefGoogle Scholar
[6]Friedman, S. D., Parameter free uniformisation, Proceedings of the American Mathematical Society, vol. 136 (2008), pp. 3327–3330.CrossRefGoogle Scholar
[7]Hamkins, J. D. and Lewis, A., Infinite time Turing machines, this Journal, vol. 65 (2000), no. 2, pp. 567–604.Google Scholar
[8]Heinatsch, C. and Möllerfeld, M., Determinacy in second order arithmetic, Foundations of the Formal Sciences V (Bold, S., Löwe, B., Räsch, Th., and van Benthem, J., editors), Studies in Logic, College Publications, London, 2007, pp. 143–155.Google Scholar
[9]Herzberger, H. G., Notes on naive semantics, Journal of Philosophical Logic, vol. 11 (1982), pp. 61–102.CrossRefGoogle Scholar
[10]John, T., Recursion in Kolmogoroff's R operator and the ordinal σ3, this Journal, vol. 51 (1986), no. 1, pp. 1–11.Google Scholar
[11]Kechris, A. S., On Spector classes, Cabal seminar 76–77 (Kechris, A. S. and Moschovakis, Y. N., editors), Lecture Notes in Mathematics Series, vol. 689, Springer, 1978, pp. 245–278.CrossRefGoogle Scholar
[12]Kreutzer, S., Partial fixed point logic on infinite structures, Annual conference of the European Association for Computer Science Logic (CLS), Lecture Notes in Computer Science, vol. 2471, Springer, 2002.Google Scholar
[13]Lubarsky, R., ITTMs with feedback, Ways of proof theory: Festschrift for W. Pohlers (Schindler, R.-D., editor), Ontos Series in Mathematical Logic, Ontos Verlag, 2010.Google Scholar
[14]Martin, D. A., Determinacy, unpublished book manuscript.Google Scholar
[15]Rathjen, M., An ordinal analysis of parameter-free Π21> comprehension, Archive for Mathematical Logic, vol. 44 (2005), no. 3, pp. 263–362.CrossRefGoogle Scholar
[16]Rathjen, M., An ordinal analysis of stability, Archive for Mathematical Logic, vol. 44 (2005), no. 1, pp. 1–62.CrossRefGoogle Scholar
[17]Sacks, G. E., Higher recursion theory, Perspectives in Mathematical Logic, Springer, 1990.CrossRefGoogle Scholar
[18]Simpson, S., Subsystems of second order arithmetic, Perspectives in Mathematical Logic, Springer, 1999.CrossRefGoogle Scholar
[19]Tanaka, K., Weak axioms of determinacy and subsystems of analysis, II. Σ20>-games, Annals of Pure and Applied Logic, vol. 52 (1991), pp. 181–193.CrossRefGoogle Scholar
[20]Welch, P. D., Eventually Infinite Time Turing degrees: infinite time decidable reals, this Journal, vol. 65 (2000), no. 3, pp. 1193–1203.Google Scholar
[21]Welch, P. D., The length of infinite time Turing machine computations, The Bulletin of the London Mathematical Society, vol. 32 (2000), pp. 129–136.CrossRefGoogle Scholar