Hostname: page-component-76fb5796d-45l2p Total loading time: 0 Render date: 2024-04-25T10:16:41.968Z Has data issue: false hasContentIssue false
  • English
  • Français

U-Lusin sets in hyperfinite time lines

Published online by Cambridge University Press:  12 March 2014

Renling Jin
Renling Jin*
Affiliation:
Department of Mathematics, University of Wisconsin, Madison, Wisconsin 53706
Get access Rights & Permissions [Opens in a new window]

Abstract

In an ω-saturated nonstandard universe a cut is an initial segment of the hyperintegers which is closed under addition. Keisler and Leth in [KL] introduced, for each given cut U, a corresponding U-topology on the hyperintegers by letting O be U-open if for any x ϵ O there is a y greater than all the elements in U such that the interval [x − y,x + y] ⊆ O. Let U be a cut in a hyperfinite time line 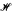, which is a hyperfinite initial segment of the hyperintegers. A subset B of 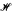is called a U-Lusin set in 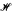if B is uncountable and for any Loeb-Borel U-meager subset X of 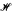, B ⋂ X is countable. Here a Loeb-Borel set is an element of the σ-algebra generated by all internal subsets of 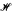: In this paper we answer some questions of Keisler and Leth about the existence of U-Lusin sets by proving the following facts. (1) If U = x/N = {y ϵ 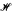: ∀n ϵ ℕ(y < x/n)} for some x ϵ 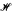, then there exists a U-Lusin set of power κ if and only if there exists a Lusin set of the reals of power κ. (2) If U ≠ x/N but the coinitiality of U is ω, then there are no U-Lusin sets if CH fails. (3) Under ZFC there exists a nonstandard universe in which U-Lusin sets exist for every cut U with uncountable cofinality and coinitiality. (4) In any ω2-saturated nonstandard universe there are no U-Lusin sets for all cuts U except U = x/N.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 57 , Issue 2 , June 1992 , pp. 528 - 533
Copyright
Copyright © Association for Symbolic Logic 1992

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[CK]Chang, C. C. and Keisler, H. J., Model theory, North-Holland, Amsterdam, 1973; 3rd ed., 1990.Google Scholar
[KKML]Keisler, H.J., Kunen, K., Miller, A. W., and Leth, S., Descriptive set theory over hyperfinite sets, this Journal, vol. 54 (1989), pp. 1167–1180.Google Scholar
[KL]Keisler, H.J. and Leth, S., Meager sets on the hyperfinite time line, this Journal, vol. 56 (1991), pp. 71–102.Google Scholar
[Lo]Loeb, P., Conversion from nonstandard to standard measure space and applications in probability theory, Transactions of the American Mathematical Society, vol. 211 (1975), pp. 113–122.CrossRefGoogle Scholar
[M1]Miller, A. W., Special subsets of the real line, Handbook of set theoretic topology (Kunen, K. and Vaughan, J. E., editors), North-Holland, Amsterdam, 1984, pp. 201–234.CrossRefGoogle Scholar
[M2]Miller, A. W., Set theoretic properties of Loeb measure, this Journal, vol. 55 (1990), pp. 1022–1036.Google Scholar
[SB]Stroyan, K. D. and Bayod, J. M., Foundations of infinitesimal stochastic analysis, North-Holland, Amsterdam, 1986.Google Scholar
[Ži]Živaljević, B., U-meaaer sets when the cofinality and the coinitiality of U are uncountable, this Journal, vol. 56 (1991), pp. 906–914.Google Scholar