Hostname: page-component-848d4c4894-jbqgn Total loading time: 0 Render date: 2024-07-03T20:39:04.957Z Has data issue: false hasContentIssue false
  • English
  • Français

The theory of the recursively enumerable weak truth-table degrees is undecidable

Published online by Cambridge University Press:  12 March 2014

Klaus Ambos-Spies ,
André Nies  and
Richard A. Shore
Klaus Ambos-Spies
Affiliation:
Mathematisches Institut, Universität Heidelberg, W-6900 Heidelberg, Germany
André Nies
Affiliation:
Mathematisches Institut, Universität Heidelberg, W-6900 Heidelberg, Germany
Richard A. Shore
Affiliation:
Department of Mathematics, Cornell University, Ithaca, New York 14853
Get access Rights & Permissions [Opens in a new window]

Abstract

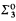We show that the partial order of -sets under inclusion is elementarily definable with parameters in the semilattice of r.e. wtt-degrees. Using a result of E. Herrmann, we can deduce that this semilattice has an undecidable theory, thereby solving an open problem of P. Odifreddi.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 57 , Issue 3 , September 1992 , pp. 864 - 874
Copyright
Copyright © Association for Symbolic Logic 1992

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[ASp,N?]Ambos-Spies, K. and Nies, A., The theory of the polynomial many-one degrees of recursive sets is undecidable (in preparation).Google Scholar
[ASp.Sh?]Ambos-Spies, K. and Shore, R., Undecidability and 1-types in the r.e. degrees (in preparation).Google Scholar
[ASp,So89]Ambos-Spies, K. and Soare, R. I., The recursively enumerable degrees have infinitely many one-types, Annals of Pure and Applied Logic, vol. 44, pp. 1–23.CrossRefGoogle Scholar
[Bu,McK81]Burris, S. and McKenzie, R., Decidability and Boolean representation, Memoir no. 246, American Mathematical Society, Providence, Rhode Island.CrossRefGoogle Scholar
[Ha,Sh82]Harrington, L. and Shelah, S., The undecidability of the recursively enumerable degrees, Bulletin (New Series) of the American Mathematical Society, vol. 6, pp. 79–80 (research announcement).Google Scholar
[He83]Herrmann, E., Definable Boolean pairs and the lattice of recursively enumerable sets, Proceedings of the first Easter conference on model theory, Seminarberichte no. 49, Sektion Mathematik, Humboldt-Universität, Berlin, pp. 42–67.Google Scholar
[He84]Herrmann, E., The undecidability of the elementary theory of the lattice of recursively enumerable sets, Proceedings of the second Frege conference at Schwerin, GDR, 1984 (Wechsung, G., editor), Mathematische Forschung, Band 20, Akademie-Verlag, Berlin, pp. 66–72.Google Scholar
[Ht,S90]Haught, C. A. and Shore, R. A., Undecidability and initial segments of the (r.e.) tt-degrees, this Journal, vol. 55, pp. 987–1006.Google Scholar
[La72]Lachlan, A. H., Embedding nondistributive lattices in the recursively enumerable degrees, Conference in mathematical logic—London '70, Lecture Notes in Mathematics, vol. 255, Springer-Verlag, Berlin, pp. 149–177.CrossRefGoogle Scholar
[Ld,Sa75]Ladner, R. and Sasso, S., The weak truth-table degrees of r.e. sets, Annals of Mathematical Logic, vol. 8, pp. 429–448.CrossRefGoogle Scholar
[Od81]Odifreddi, P., Strong reducibilities, Bulletin (New Series) of the American Mathematical Society, vol. 4, pp. 37–86.CrossRefGoogle Scholar
[Od89]Odifreddi, P., Classical recursion theory, North-Holland, Amsterdam.Google Scholar
[So87]Soare, R. I., Recursively enumerable sets and degrees, Springer-Verlag, Berlin.CrossRefGoogle Scholar