Article contents
STRUCTURE THEORY OF L(ℝ, μ) AND ITS APPLICATIONS
Published online by Cambridge University Press: 13 March 2015
Abstract
In this paper, we explore the structure theory of L(ℝ, μ) under the hypothesis L(ℝ, μ) ⊧ “AD + μ is a normal fine measure on 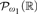 ” and give some applications. First we show that “ ZFC + there exist ω2 Woodin cardinals”1 has the same consistency strength as “ AD + ω1 is ℝ-supercompact”. During this process we show that if L(ℝ, μ) ⊧ AD then in fact L(ℝ, μ) ⊧ AD+. Next we prove important properties of L(ℝ, μ) including Σ1 -reflection and the uniqueness of μ in L(ℝ, μ). Then we give the computation of full HOD in L(ℝ, μ). Finally, we use Σ1 -reflection and ℙmax forcing to construct a certain ideal on
” and give some applications. First we show that “ ZFC + there exist ω2 Woodin cardinals”1 has the same consistency strength as “ AD + ω1 is ℝ-supercompact”. During this process we show that if L(ℝ, μ) ⊧ AD then in fact L(ℝ, μ) ⊧ AD+. Next we prove important properties of L(ℝ, μ) including Σ1 -reflection and the uniqueness of μ in L(ℝ, μ). Then we give the computation of full HOD in L(ℝ, μ). Finally, we use Σ1 -reflection and ℙmax forcing to construct a certain ideal on 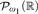 (or equivalently on
(or equivalently on 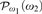 in this situation) that has the same consistency strength as “ZFC+ there exist ω2 Woodin cardinals.”
in this situation) that has the same consistency strength as “ZFC+ there exist ω2 Woodin cardinals.”
- Type
- Articles
- Information
- Copyright
- Copyright © The Association for Symbolic Logic 2015
References
REFERENCES
- 4
- Cited by


