Article contents
Stable embeddedness and NIP
Published online by Cambridge University Press: 12 March 2014
Abstract
We give some sufficient conditions for a predicate P in a complete theory T to be “stably embedded”. Let 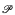 be P with its “induced ∅-definable structure”. The conditions are that
be P with its “induced ∅-definable structure”. The conditions are that 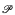 (or rather its theory) is “rosy”. P has NIP in T and that P is stably 1-embedded in T. This generalizes a recent result of Hasson and Onshuus [6] which deals with the case where P is o-minimal in T. Our proofs make use of the theory of strict nonforking and weight in NIP theories ([3], [10]).
(or rather its theory) is “rosy”. P has NIP in T and that P is stably 1-embedded in T. This generalizes a recent result of Hasson and Onshuus [6] which deals with the case where P is o-minimal in T. Our proofs make use of the theory of strict nonforking and weight in NIP theories ([3], [10]).
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 2011
References
REFERENCES
- 6
- Cited by


