Hostname: page-component-848d4c4894-wzw2p Total loading time: 0 Render date: 2024-05-04T16:39:52.147Z Has data issue: false hasContentIssue false
  • English
  • Français

A special class of almost disjoint families

Published online by Cambridge University Press:  12 March 2014

Thomas E. Leathrum
Thomas E. Leathrum*
Affiliation:
Department of Mathematics and Computer Science, Dartmouth College, Hanover, New Hampshire 03755
*
Department of Mathematical Sciences, Berry College, Mt. Berry, Georgia 30149, E-mail: tleathrum@berry.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

The collection of branches (maximal linearly ordered sets of nodes) of the tree <ωω (ordered by inclusion) forms an almost disjoint family (of sets of nodes). This family is not maximal — for example, any level of the tree is almost disjoint from all of the branches. How many sets must be added to the family of branches to make it maximal? This question leads to a series of definitions and results: a set of nodes is off-branch if it is almost disjoint from every branch in the tree; an off-branch family is an almost disjoint family of off-branch sets; and 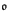is the minimum cardinality of a maximal off-branch family.

Results concerning 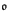include: (in ZFC) 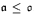, and (consistent with ZFC) 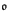is not equal to any of the standard small cardinal invariants 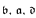or 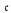= 2ω. Most of these consistency results use standard forcing notions—for example, 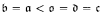in the Cohen model.

Many interesting open questions remain, though—for example, whether .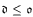

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 60 , Issue 3 , September 1995 , pp. 879 - 891
Copyright
Copyright © Association for Symbolic Logic 1995

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[BS]Balcar, Bohuslav and Simon, Petr, Disjoint refinement, Handbook of Boolean algebras (Monk, J. Donald and Bonnet, Robert, editors), vol. 2, North-Holland, New York, 1989, pp. 333–386.Google Scholar
[Fr]Fremlin, D. H., Consequences of Martin's axiom, Cambridge University Press, New York, 1984.CrossRefGoogle Scholar
[Je]Jech, Thomas J., Multiple forcing, Cambridge University Press, New York, 1986.Google Scholar
[Ku]Kunen, Kenneth, Set theory: an introduction to independence proofs, North-Holland, New York, 1980.Google Scholar
[Sh]Shelah, Saharon, On cardinal invariants of the continuum, Axiomatic set theory, Contemporary Mathematics, vol. 31, American Mathematical Society, Providence, Rhode Island, 1984, pp. 183–207.CrossRefGoogle Scholar
[So]Solovay, Robert M., A model of set-theory in which every set of reals is Lebesgue measurable, Annals of Mathematics, ser. 2, vol. 92 (1970), pp. 1–56.CrossRefGoogle Scholar
[Va]Vaughan, Jerry E., Small uncountable cardinals and topology, Open problems in topology (van Mill, J. and Reed, G. M., editors), North-Holland, New York, 1990, pp. 195–218.Google Scholar
[vD]van Douwen, Erik K., The integers and topology, Handbook of set theoretic topology (Kunen, K. and Vaughan, J. E., editors), North-Holland, New York, 1984, pp. 111–168.CrossRefGoogle Scholar