Article contents
Scott incomplete Boolean ultrapowers of the real line
Published online by Cambridge University Press: 12 March 2014
Abstract
An ordered field is said to be Scott complete iff it is complete with respect to its uniform structure. Zakon has asked whether nonstandard real lines are Scott complete. We prove in ZFC that for any complete Boolean algebra B which is not (ω, 2)-distributive there is an ultrafilter 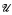 of B such that the Boolean ultrapower of the real line modulo
of B such that the Boolean ultrapower of the real line modulo 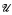 is not Scott complete. We also show how forcing in set theory gives rise to examples of Boolean ultrapowers of the real line which are not Scott complete.
is not Scott complete. We also show how forcing in set theory gives rise to examples of Boolean ultrapowers of the real line which are not Scott complete.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1995
References
REFERENCES
- 3
- Cited by




