Article contents
Scales in K(ℝ) at the end of a weak gap
Published online by Cambridge University Press: 12 March 2014
Extract
In this note we shall prove
Theorem 0.1. Let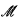 be a countably ω-iterable
be a countably ω-iterable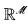 -mouse which satisfies AD, and [α, β] a weak gap of
-mouse which satisfies AD, and [α, β] a weak gap of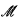 . Suppose
. Suppose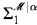 is captured by mice with iteration strategies in
is captured by mice with iteration strategies in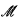 ∣α. Let n be least such that
∣α. Let n be least such that 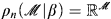 ; then we have that
; then we have that 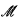 believes that
believes that 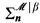 has the Scale Property.
has the Scale Property.
This complements the work of [5] on the construction of scales of minimal complexity on sets of reals in K(ℝ). Theorem 0.1 was proved there under the stronger hypothesis that all sets definable over 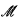 are determined, although without the capturing hypothesis. (See [5, Theorem 4.14].) Unfortunately, this is more determinacy than would be available as an induction hypothesis in a core model induction. The capturing hypothesis, on the other hand, is available in such a situation. Since core model inductions are one of the principal applications of the construction of optimal scales, it is important to prove 0.1 as stated.
are determined, although without the capturing hypothesis. (See [5, Theorem 4.14].) Unfortunately, this is more determinacy than would be available as an induction hypothesis in a core model induction. The capturing hypothesis, on the other hand, is available in such a situation. Since core model inductions are one of the principal applications of the construction of optimal scales, it is important to prove 0.1 as stated.
Our proof will incorporate a number of ideas due to Woodin which figure prominently in the weak gap case of the core model induction. It relies also on the connection between scales and iteration strategies with the Dodd-Jensen property first discovered in [3]. Let 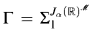 be the pointclass at the beginning of the weak gap referred to in 0.1. In section 1, we use Woodin's ideas to construct a Γ-full a mouse
be the pointclass at the beginning of the weak gap referred to in 0.1. In section 1, we use Woodin's ideas to construct a Γ-full a mouse 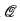 having ω Woodin cardinals cofinal in its ordinals, together with an iteration strategy Σ which condenses well in the sense of [4, Def. 1.13]. In section 2, we construct the desired scale from
having ω Woodin cardinals cofinal in its ordinals, together with an iteration strategy Σ which condenses well in the sense of [4, Def. 1.13]. In section 2, we construct the desired scale from 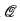 and Σ.
and Σ.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 2008
References
REFERENCES
- 10
- Cited by


