Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Rinot, Assaf
2009.
A cofinality-preserving small forcing may introduce a special Aronszajn tree.
Archive for Mathematical Logic,
Vol. 48,
Issue. 8,
p.
817.
Rinot, Assaf
2014.
The Ostaszewski square and homogeneous Souslin trees.
Israel Journal of Mathematics,
Vol. 199,
Issue. 2,
p.
975.
Matet, Pierre
2015.
Guessing more sets.
Annals of Pure and Applied Logic,
Vol. 166,
Issue. 10,
p.
953.
Rinot, Assaf
2017.
Higher Souslin trees and the GCH, revisited.
Advances in Mathematics,
Vol. 311,
Issue. ,
p.
510.
Lambie‐Hanson, Chris
2017.
Aronszajn trees, square principles, and stationary reflection.
Mathematical Logic Quarterly,
Vol. 63,
Issue. 3-4,
p.
265.
Fuchs, G.
and
Rinot, A.
2018.
Weak square and stationary reflection.
Acta Mathematica Hungarica,
Vol. 155,
Issue. 2,
p.
393.
Lambie-Hanson, Chris
and
Rinot, Assaf
2018.
Knaster and friends I: closed colorings and precalibers.
Algebra universalis,
Vol. 79,
Issue. 4,
Matet, Pierre
2018.
Scales with various kinds of good points.
Mathematical Logic Quarterly,
Vol. 64,
Issue. 4-5,
p.
349.
Matsubara, Yo
Sakai, Hiroshi
and
Usuba, Toshimichi
2019.
On the existence of skinny stationary subsets.
Annals of Pure and Applied Logic,
Vol. 170,
Issue. 5,
p.
539.
Brodsky, Ari Meir
and
Rinot, Assaf
2019.
A Remark on Schimmerling’s Question.
Order,
Vol. 36,
Issue. 3,
p.
525.
Du, Jin
2019.
Diamond, scales and GCH down to $$\aleph _{\omega ^2}$$ ℵ ω 2.
Archive for Mathematical Logic,
Vol. 58,
Issue. 3-4,
p.
427.
Matet, Pierre
2021.
Towers and clubs.
Archive for Mathematical Logic,
Vol. 60,
Issue. 6,
p.
683.
Matet, Pierre
2021.
Meeting numbers and pseudopowers.
Mathematical Logic Quarterly,
Vol. 67,
Issue. 1,
p.
59.
Rinot, Assaf
2022.
On the ideal J[κ].
Annals of Pure and Applied Logic,
Vol. 173,
Issue. 2,
p.
103055.
LAMBIE-HANSON, CHRIS
and
RINOT, ASSAF
2023.
KNASTER AND FRIENDS III: SUBADDITIVE COLORINGS.
The Journal of Symbolic Logic,
Vol. 88,
Issue. 3,
p.
1230.
Zhang, Jing
2023.
Reflection principles, GCH and the uniformization properties.
Israel Journal of Mathematics,
Vol. 254,
Issue. 1,
p.
57.
Rinot, Assaf
Yadai, Shira
and
You, Zhixing
2024.
Full Souslin trees at small cardinals.
Journal of the London Mathematical Society,
Vol. 110,
Issue. 1,
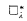 together with 2λ = λ+ implies ⋄S for every S ⊆ λ+ that reflects stationarily often.
together with 2λ = λ+ implies ⋄S for every S ⊆ λ+ that reflects stationarily often.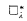 implies that I[S; λ] is fat for every S ⊆ λ+ that reflects stationarily often;
implies that I[S; λ] is fat for every S ⊆ λ+ that reflects stationarily often;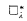 fails, while I[S; λ] is fat for every stationary S ⊆ λ+ that reflects stationarily often.
fails, while I[S; λ] is fat for every stationary S ⊆ λ+ that reflects stationarily often.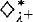 is studied as well.
is studied as well.

