Article contents
The positive properties of isolic integers
Published online by Cambridge University Press: 12 March 2014
Extract
In this paper we show (cf. Theorem 22) that in a language L* with equality, whose relation symbols denote arbitrary relations over ω* (=rational integers) and whose function symbols denote 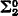 (= ∃∀ definable in the arithmetic hierarchy) functions over ω*, (i) a positive sentence is true in Λ* (= isolic integers) iff some Horn reduct is true in ω* with
(= ∃∀ definable in the arithmetic hierarchy) functions over ω*, (i) a positive sentence is true in Λ* (= isolic integers) iff some Horn reduct is true in ω* with 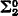 Skolem functions. We also show (cf Theorem 20) that (ii) a universally quantified sentence is true in Λ* iff some Horn reduct is true in Λ*.The latter result is nontrivial because our relations are arbitrary and our functions are
Skolem functions. We also show (cf Theorem 20) that (ii) a universally quantified sentence is true in Λ* iff some Horn reduct is true in Λ*.The latter result is nontrivial because our relations are arbitrary and our functions are 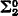 In order to obtain (i) it was necessary to generalize the frame extensions of [7]. This is done in §2. Our extension procedure agrees with that of [7] for recursive relations (cf. Theorem 12), and is certainly more general for
In order to obtain (i) it was necessary to generalize the frame extensions of [7]. This is done in §2. Our extension procedure agrees with that of [7] for recursive relations (cf. Theorem 12), and is certainly more general for 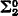 −
−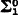 relations. What happens in the
relations. What happens in the 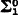 case is still open. In §3 we develop the basic properties of our extension so that in §4 we can prove a metatheorem (cf. Theorems 8 and 10) about Λ (=isols), in a language L with equality whose relation symbols denote arbitrary relations over ω (=nonnegative integers) and whose function symbols denote almost R↑ combinatorial functions. In Theorem 11 this is generalized to infinitary universal sentences. In §5 generic isols are introduced. These are used (cf. Theorems 16–19) to generalize and simplify the “fundamental lemma” of [8]. The basic induction is patterned after Lemma 4.1 of [8], but is stronger in that any sufficiently generic assignment attainable from a frame yields
case is still open. In §3 we develop the basic properties of our extension so that in §4 we can prove a metatheorem (cf. Theorems 8 and 10) about Λ (=isols), in a language L with equality whose relation symbols denote arbitrary relations over ω (=nonnegative integers) and whose function symbols denote almost R↑ combinatorial functions. In Theorem 11 this is generalized to infinitary universal sentences. In §5 generic isols are introduced. These are used (cf. Theorems 16–19) to generalize and simplify the “fundamental lemma” of [8]. The basic induction is patterned after Lemma 4.1 of [8], but is stronger in that any sufficiently generic assignment attainable from a frame yields 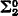 Skolem functions. Finally in §6 these results are applied to Λ*, yielding the titled result (i) of our paper. Immediately following Theorem 15 there is a discussion which attempts to justify the way we extend relations to Λ.
Skolem functions. Finally in §6 these results are applied to Λ*, yielding the titled result (i) of our paper. Immediately following Theorem 15 there is a discussion which attempts to justify the way we extend relations to Λ.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1972
References
REFERENCES
- 3
- Cited by




