Article contents
On n-quantifier induction
Published online by Cambridge University Press: 12 March 2014
Extract
In this paper we discuss subsystems of number theory based on restrictions on induction in terms of quantifiers, and we show that all the natural formulations of ‘n-quantifier induction’ are reducible to one of two (for n ≠ 0) nonequivalent normal forms: the axiom of induction restricted to 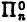 (or, equivalently,
(or, equivalently, 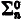 ) formulae and the rule of induction restricted to
) formulae and the rule of induction restricted to 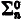 formulae.
formulae.
Let Z0 be classical elementary number theory with a symbol and defining equations for each Kalmar elementary function, and the rule of induction

restricted to quantifier-free formulae. Given the schema
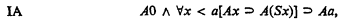
let IAn be the restriction of IA to formulae of Z0 with ≤n nested quantifiers, IAn′ to formulae with ≤n nested quantifiers, disregarding bounded quantifiers, 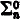 the restriction to
the restriction to 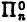 formulae,
formulae, 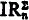 the restriction to
the restriction to 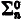 , formulae. IRn, IRn′,
, formulae. IRn, IRn′, 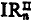 ,
, 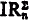 are analogous.
are analogous.
Then, we show that, for every n, 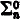 ,
, 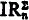 , IAn, and IAn′, are all equivalent modulo Z0. The corresponding statement does not hold for IR. We show that, if n ≠ 0,
, IAn, and IAn′, are all equivalent modulo Z0. The corresponding statement does not hold for IR. We show that, if n ≠ 0, 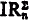 is reducible to
is reducible to 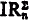 ; evidently IRn is reducible to
; evidently IRn is reducible to 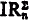 . On the other hand, IRn′ is obviously equivalent to IAn′ [10, Lemma 2].
. On the other hand, IRn′ is obviously equivalent to IAn′ [10, Lemma 2].
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1972
References
REFERENCES
- 56
- Cited by


