Article contents
Nowhere simple sets and the lattice of recursively enumerable sets1
Published online by Cambridge University Press: 12 March 2014
Extract
Ever since Post [4] the structure of recursively enumerable sets and their classification has been an important area in recursion theory. It is also intimately connected with the study of the lattices 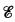 and
and 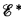 of r.e. sets and r.e. sets modulo finite sets respectively. (This lattice theoretic viewpoint was introduced by Myhill [3].) Key roles in both areas have been played by the lattice of r.e. supersets,
of r.e. sets and r.e. sets modulo finite sets respectively. (This lattice theoretic viewpoint was introduced by Myhill [3].) Key roles in both areas have been played by the lattice of r.e. supersets, 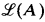 , of an r.e. set A (along with the corresponding
, of an r.e. set A (along with the corresponding 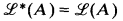 modulo finite sets) and more recently by the group of automorphisms of
modulo finite sets) and more recently by the group of automorphisms of 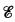 and
and 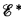 . Thus for example we have Lachlan's deep result [1] that Post's notion of A being hyperhypersimple is equivalent to
. Thus for example we have Lachlan's deep result [1] that Post's notion of A being hyperhypersimple is equivalent to 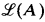 (or
(or 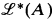 ) being a Boolean algebra. Indeed Lachlan even tells us which Boolean algebras appear as
) being a Boolean algebra. Indeed Lachlan even tells us which Boolean algebras appear as 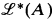 —precisely those with Σ3 representations. There are also many other simpler but still illuminating connections between the older typology of r.e. sets and their roles in the lattice
—precisely those with Σ3 representations. There are also many other simpler but still illuminating connections between the older typology of r.e. sets and their roles in the lattice 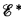 . (r-maximal sets for example are just those with
. (r-maximal sets for example are just those with 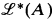 completely uncomplemented.) On the other hand, work on automorphisms by Martin and by Soare [8], [9] has shown that most other Post type conditions on r.e. sets such as hypersimplicity or creativeness which are not obviously lattice theoretic are in fact not invariant properties of
completely uncomplemented.) On the other hand, work on automorphisms by Martin and by Soare [8], [9] has shown that most other Post type conditions on r.e. sets such as hypersimplicity or creativeness which are not obviously lattice theoretic are in fact not invariant properties of 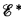 .
.
In general the program of analyzing and classifying r.e. sets has been directed at the simple sets. Thus the subtypes of simple sets studied abound — between ten and fifteen are mentioned in [5] and there are others — but there seems to be much less known about the nonsimple sets. The typologies introduced for the nonsimple sets begin with Post's notion of creativeness and add on a few variations. (See [5, §8.7] and the related exercises for some examples.) Although there is a classification scheme for r.e. sets along the simple to creative line (see [5, §8.7]) it is admitted to be somewhat artificial and arbitrary. Moreover there does not seem to have been much recent work on the nonsimple sets.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1978
Footnotes
The preparation of this paper was partially supported by NSF Grant MCS74–06378. We would also like to thank A. Nerode and R. Soare for helpful discussions about some of the material presented here.
References
BIBLIOGRAPHY
- 22
- Cited by


