We make comments on some problems Erdős and Hajnal posed in their famous problem list. Let X be a graph on 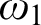$\omega _1$ with the property that every uncountable set A of vertices contains a finite set s such that each element of 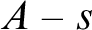$A-s$ is joined to one of the elements of s. Does then X contain an uncountable clique? (Problem 69) We prove that both the statement and its negation are consistent. Do there exist circuitfree graphs 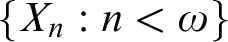$\{X_n:n<\omega \}$ on 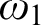$\omega _1$ such that if 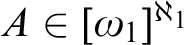$A\in [\omega _1]^{\aleph _1}$ , then 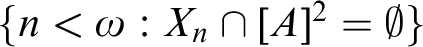$\{n<\omega :X_n\cap [A]^2=\emptyset \}$ is finite? (Problem 61) We show that the answer is yes under CH, and no under Martin’s axiom. Does there exist 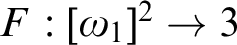$F:[\omega _1]^2\to 3$ with all three colors appearing in every uncountable set, and with no triangle of three colors. (Problem 68) We give a different proof of Todorcevic’ theorem that the existence of a 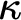$\kappa $ -Suslin tree gives 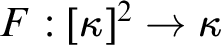$F:[\kappa ]^2\to \kappa $ establishing 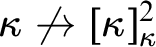$\kappa \not \to [\kappa ]^2_{\kappa }$ with no three-colored triangles. 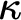This statement in turn implies the existence of a $\kappa $ -Aronszajn tree.