Article contents
A minimal Prikry-type forcing for singularizing a measurable cardinal
Published online by Cambridge University Press: 12 March 2014
Abstract
Recently, Gitik, Kanovei and the first author proved that for a classical Prikry forcing extension the family of the intermediate models can be parametrized by 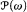 /finite. By modifying the standard Prikry tree forcing we define a Prikry-type forcing which also singularizes a measurable cardinal but which is minimal, i.e., there are no intermediate models properly between the ground model and the generic extension. The proof relies on combining the rigidity of the tree structure with indiscernibility arguments resulting from the normality of the associated measures.
/finite. By modifying the standard Prikry tree forcing we define a Prikry-type forcing which also singularizes a measurable cardinal but which is minimal, i.e., there are no intermediate models properly between the ground model and the generic extension. The proof relies on combining the rigidity of the tree structure with indiscernibility arguments resulting from the normality of the associated measures.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 2013
References
REFERENCES
- 5
- Cited by


