Hostname: page-component-848d4c4894-4rdrl Total loading time: 0 Render date: 2024-06-27T15:08:14.281Z Has data issue: false hasContentIssue false
  • English
  • Français

Measurable chromatic numbers

Published online by Cambridge University Press:  12 March 2014

Benjamin D. Miller
Benjamin D. Miller*
Affiliation:
UCLA Mathematics Department, Box 951555, Los Angeles, CA 90095-1555., USA, E-mail: bdm@math.ucla.edu, URL: http://www.math.ucla.edu/~bdm
Get access Rights & Permissions [Opens in a new window]

Abstract

We show that if add(null) = c, then the globally Baire and universally measurable chromatic numbers of the graph of any Borel function on a Polish space are equal and at most three. In particular, this holds for the graph of the unilateral shift on [ℕ]ℕ, although its Borel chromatic number is ℵ0. We also show that if add(null) = c, then the universally measurable chromatic number of every treeing of a measure amenable equivalence relation is at most three. In particular, this holds for “the” minimum analytic graph 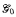with uncountable Borel (and Baire measurable) chromatic number. In contrast, we show that for all κ Є6 (2, 3…..ℵ0, c), there is a treeing of E0 with Borel and Baire measurable chromatic number κ. Finally, we use a Glimm–Effros style dichotomy theorem to show that every basis for a non-empty initial segment of the class of graphs of Borel functions of Borel chromatic number at least three contains a copy of (ℝ<ℕ, ⊇).

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 73 , Issue 4 , December 2008 , pp. 1139 - 1157
Copyright
Copyright © Association for Symbolic Logic 2008

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Bartoszynski, Tomek, Additivity of measure implies additivity of category. Transactions of the American Mathematical Society, vol. 281 (1984), no. 1, pp. 209–213.CrossRefGoogle Scholar
[2]Dougherty, R., Jackson, S., and Kechris, A. S., The structure of hyperfinite Borel equivalence relations, Transactions of the American Mathematical Society, vol. 341 (1994), no. 1, pp. 193–225.CrossRefGoogle Scholar
[3]Eigen, S., Hajian, A., and Weiss, B., Borel automorphisms with no finite invariant measure, Proceedings of the American Mathematical Society, vol. 126 (1998), no. 12, pp. 3619–3623.CrossRefGoogle Scholar
[4]Harrington, L. A., Kechris, A. S., and Louveau, A., A Glimm–Effros dichotomy for Borel equivalence relations, Journal of the American Mathematical Society, vol. 3 (1990), no. 4, pp. 903–928.CrossRefGoogle Scholar
[5]Hjorth, G. and Miller, B. D., Ends of graphed equivalence relations, II, Israel Journal of Mathematics, to appear.Google Scholar
[6]Jackson, S., Kechris, A. S., and Louveau, A., Countable Borel equivalence relations, Journal of Mathematical Logic, vol. 2 (2002), no. 1, pp. 1–80.CrossRefGoogle Scholar
[7]Kechris, A. S., Classical descriptive set theory, Graduate Texts in Mathematics, vol. 156, SpringerVerlag, New York, 1995.CrossRefGoogle Scholar
[8]Kechris, A. S. and Miller, B. D., Topics in orbit equivalence. Lecture Notes in Mathematics, vol. 1852, Springer-Verlag, Berlin, 2004.CrossRefGoogle Scholar
[9]Kechris, A. S. and Miller, B. D., Means an equivalence relations, Israel Journal of Mathematics, vol. 163 (2008), pp. 241–262.CrossRefGoogle Scholar
[10]Kechris, A. S., Solecki, S., and Todorcevic, S., Borel chromatic numbers, Advances in Mathematics, vol. 141 (1999), no. 1, pp. 1–44.CrossRefGoogle Scholar
[11]Lecomte, D. and Miller, B. D., Basis theorems for non-potentially closed sets and graphs of uncountable Borel chromatic number, preprint, 2007.CrossRefGoogle Scholar
[12]Louveau, A., Some dichotomy results for analytic graphs, preprint, 2001.Google Scholar
[13]Martin, D.A. and Solovay, R.M., Internal Cohen extensions, Annals of Mathematical Logic, vol. 2 (1970), no. 2, pp. 143–178.CrossRefGoogle Scholar
[14]Miller, B. D., Ends of graphed equivalence relations. I, Israel Journal of Mathematics, to appear.Google Scholar
[15]Miller, B. D., On the existence of quasi-invariant measures of a given cocycle, Ergodic Theory of Dynamic Systems, to appear.Google Scholar
[16]Miller, B. D. and Rosendal, C., Descriptive Kakutani equivalence, Journal of the European Mathematical Society, to appear.Google Scholar
[17]Oxtoby, J., Measure and category, Springer-Verlag, 1971.CrossRefGoogle Scholar