Article contents
Maximal irredundance and maximal ideal independence in Boolean algebras
Published online by Cambridge University Press: 12 March 2014
Extract
Recall that a subset X of an algebra A is irredundant iff x ∉ 〈X∖{x}〉 for all x ϵ X, where 〈X∖{x}) is the subalgebra generated by X∖{x}. By Zorn's lemma there is always a maximal irredundant set in an algebra. This gives rise to a natural cardinal function Irrmm(A) = min{∣X∣: X is a maximal irredundant subset of A}. The first half of this article is devoted to proving that there is an atomless Boolean algebra A of size 2ω for which Irrmm(A) = ω.
A subset X of a BA A is ideal independent iff x ∉ (X∖{x}〉id for all x ϵ X, where 〈X∖{x}〉id is the ideal generated by X∖{x}. Again, by Zorn's lemma there is always a maximal ideal independent subset of any Boolean algebra. We then consider two associated functions. A spectrum function
Sspect(A) = {∣X∣: X is a maximal ideal independent subset of A}
and the least element of this set, smm(A). We show that many sets of infinite cardinals can appear as Sspect(A). The relationship of Smm to similar “continuum cardinals” is investigated. It is shown that it is relatively consistent that Smm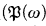 /fin) < 2ω.
/fin) < 2ω.
We use the letter s here because of the relationship of ideal independence with the well-known cardinal invariant spread; see Monk [5]. Namely, sup{∣X∣: X is ideal independent in A} is the same as the spread of the Stone space Ult(A); the spread of a topological space X is the supremum of cardinalities of discrete subspaces.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 2008
References
REFERENCES
- 2
- Cited by


