Hostname: page-component-848d4c4894-jbqgn Total loading time: 0 Render date: 2024-06-22T13:37:41.132Z Has data issue: false hasContentIssue false
  • English
  • Français

Low Level Nondelegability Results: Domination and Recursive Enumeration

Published online by Cambridge University Press:  12 March 2014

Mingzhong Cai  and
Richard A. Shore
Mingzhong Cai
Affiliation:
Department of Mathematics, University of Wisconsin, Madison WI 53705, USA, E-Mail: mcai@math.wisc.edu
Richard A. Shore
Affiliation:
Department of Mathematics, Cornell University, Ithaca NY 14853, USA, E-mail: shore@math.cornell.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

We study low level nondefinability in the Turing degrees. We prove a variety of results, including, for example, that being array nonrecursive is not definable by a Σ1 or Π1 formula in the language (≤, REA) where REA stands for the “r.e. in and above” predicate. In contrast, this property is definable by a Π2 formula in this language. We also show that the Σ1-theory of (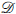, ≤, REA) is decidable.

Keywords

03D28
Type
Research Article
Information
The Journal of Symbolic Logic , Volume 78 , Issue 3 , September 2013 , pp. 1005 - 1024
Copyright
Copyright © Association for Symbolic Logic 2013

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1] Cai, M., A hyperimmune minimal degree and an ANR 2-minimal degree, Notre Dame Journal of Formal Logic, vol. 51 (2010), no. 4, pp. 443–455.Google Scholar
[2] Cai, M., Array nonrecursiveness and relative recursive enumerability, this Journal, vol. 77 (2012), pp. 21–32.Google Scholar
[3] Cai, M. and Shore, R. A., Domination, forcing, array nonrecursiveness and relative recursive enumerability, this Journal, vol. 77 (2012), pp. 33–48.Google Scholar
[4] Downey, R., Jockusch, C., and Stob, M., Array nonrecursive degrees and genericity, London Mathematical Society Lecture Note Series 224, Cambridge University Press, 1996.Google Scholar
[5] Friedberg, R. M., A criterion for completeness of degrees of unsolvability, this Journal, vol. 22 (1957), pp. 159–160.Google Scholar
[6] Hinman, P. G. and Slaman, T. A., Jump embeddings in the Turing degrees, this Journal, vol. 56 (1991), pp. 563–591.Google Scholar
[7] Jockusch, C., The degrees of hyperhyperimmune sets, this Journal, vol. 34 (1969), no. 3, pp. 489–493.Google Scholar
[8] Jockusch, C. G., Degrees of generic sets, Recursion theory: its generalisations and applications (Drake, F. R. and Wainer, S. S., editors), Cambridge University Press, 1980, pp. 110–139.Google Scholar
[9] Jockusch, C. G. Jr., and Shore, R. A., Pseudo-jump operators II: transfinite iterations, hierarchies andminimal covers, this Journal, vol. 49 (1984), pp. 1205–1236.Google Scholar
[10] Lerman, M., Degrees of unsolvability: Local and global theory, Perspectives in Mathematical Logic, vol. 11, Springer-Verlag, 1983.Google Scholar
[11] Lerman, M. and Shore, R. A., Decidability and invariant classes for degree structures, Transactions of the American Mathematical Society, vol. 310 (1988), pp. 669–692.Google Scholar
[12] Miller, W. and Martin, D. A., The degrees of hyperimmune sets, Zeitschrift fur Mathematische Logik und Grundlagen der Mathematik, vol. 14 (1968), pp. 159–166.Google Scholar
[13] Montalbán, A., Embedding jump upper semilattices into the Turing degrees, this Journal, vol. 68 (2003), no. 3, pp. 989–1014.Google Scholar
[14] Schaeffer, B., Dynamic notions of genericity and array noncomputability, Annals of Pure and Applied Logic, vol. 95 (1998), pp. 37–69.Google Scholar
[15] Shore, R. A., Minimal degrees which are but not , Proceedings of the American Mathematical Society, vol. 132 (2004), pp. 563–565.Google Scholar
[16] Shore, R. A., Direct and local definitions of the Turing jump, Journal of Mathematical Logic, vol. 7 (2007), pp. 229–262.Google Scholar
[17] Shore, R. A. and Slaman, T. A., Defining the Turing jump, Mathematical Research Letters, vol. 6 (1999), pp. 711–722.Google Scholar
[18] Slaman, T. A., Global properties of the Turing degrees and the Turing jump, Computational prospects of infinity, Part I, Tutorials, Lecture Notes Series. Institute for Mathematical Sciences. National University of Singapore, World Science Publishers, Hackensack, NJ, 2008, pp. 83–101.Google Scholar
[19] Soare, R. I., Recursively enumerable sets and degrees, Perspectives in Mathematical Logic, Springer-Verlag, Berlin, 1987.Google Scholar
[20] Spector, C., On degrees of recursive unsolvability, Annals of Mathematics, vol. 64 (1956), no. 3, pp. 581–592.Google Scholar