Hostname: page-component-77c89778f8-cnmwb Total loading time: 0 Render date: 2024-07-22T23:43:47.292Z Has data issue: false hasContentIssue false
  • English
  • Français

Lattice initial segments of the hyperdegrees

Published online by Cambridge University Press:  12 March 2014

Richard A. Shore  and
Bjørn Kjos-Hanssen
Richard A. Shore
Affiliation:
Department of Mathematics, Cornell University, Ithaca, NY 14853, USA, E-mail: shore@math.cornell.edu
Bjørn Kjos-Hanssen
Affiliation:
Department of Mathematics, University of Hawai'i at Mānoa, Honolulu, HI 96822, USA, E-mail: bjoern@math.hawaii.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

We affirm a conjecture of Sacks [1972] by showing that every countable distributive lattice is isomorphic to an initial segment of the hyperdegrees, 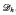. In fact, we prove that every sublattice of any hyperarithmetic lattice (and so, in particular, every countable, locally finite lattice) is isomorphic to an initial segment of 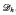. Corollaries include the decidability of the two quantifier theory of 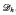, and the undecidability of its three quantifier theory. The key tool in the proof is a new lattice representation theorem that provides a notion of forcing for which we can prove a version of the fusion lemma in the hyperarithmetic setting and so the preservation of ω1ck. Somewhat surprisingly, the set theoretic analog of this forcing does not preserve ω1. On the other hand, we construct countable lattices that are not isomorphic to any initial segment of .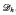

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 75 , Issue 1 , March 2010 , pp. 103 - 130
Copyright
Copyright © Association for Symbolic Logic 2010

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Abraham, U. and Shore, R. A. [1986], Initial segments of the degrees of size ℵ1 , Israel Journal of Mathematics, vol. 53, pp. 1–51.Google Scholar
Abraham, U. and Shore, R. A. [1986a], The degrees of constructibility below a Cohen real, Journal of the London Mathematical Society, vol. 53, no. 3, pp. 193–208.CrossRefGoogle Scholar
Adamowicz, A. [1976], On finite lattices of degrees of constructibility, this Journal, vol. 41, pp. 313–322.Google Scholar
Adamowicz, A. [1977], Constructible semi-lattices of degrees of constructibility, Set theory and hierarchy theory V (Lachlan, , Srebny, , and Zarach, , editors), Lecture Notes in Mathematics, vol. 619, Springer-Verlag, Berlin.Google Scholar
Balcar, B. and Hajek, P. [1978], On sequences of degrees of constructibility, Zeitschriftfur Mathematische Logik und Grundlagen der Mathematik, vol. 24, pp. 291–296.Google Scholar
Cohen, P. [1966], Set theory and the continuum hypothesis, Benjamin, New York.Google Scholar
Dorais, F. [2007], Souslin trees and degrees of constructibility, Ph.D. thesis, Dartmouth College.Google Scholar
Farrington, P. [1983], Hinges and automorphisms of the degrees of constructibility, Journal of the London Mathematical Society, vol. 28, no. 2, pp. 193–202.CrossRefGoogle Scholar
Farrington, P. [1984], First order theory of the c-degrees, Zeitschrift für Mathematische Logik und Grundlagen der Mathematik, vol. 30, pp. 437–446.Google Scholar
Feferman, S. [1965], Some applications of the notion of forcing and generic sets, Fundamenta Mathematical vol. 56, pp. 325–345.Google Scholar
Gandy, R. O. and Sacks, G. E. [1967], A minimal hyperdegree, Fundamenta Mathematicae, vol. 61, pp. 215–223.Google Scholar
Grätzer, G. [2003], General lattice theory, 2nd ed., Birkhäuser Verlag, Basel.Google Scholar
Groszek, M. S. and Shore, R. A. [1988], Initial segments of the degrees of constructibility, Israel Journal of Mathematics, vol. 63, pp. 149–177.CrossRefGoogle Scholar
Groszek, M. S. and Slaman, T. A. [1983], Independence results on the global structure of the Turing degrees, Transactions of the American Mathematical Society, vol. 277, pp. 579–588.Google Scholar
Hodges, W. [1993], Model theory, Encyclopedia of Mathematics and its Applications, vol. 42, Cambridge University Press, Cambridge, England.Google Scholar
Jónsson, B. [1953], On the representations of lattices, Mathematica Scandinavica, vol. 1, pp. 193–206.Google Scholar
Kjos-Hanssen, B. [2002], Lattice initial segments of the Turing degrees, Ph.D. thesis, University of California, Berkeley.Google Scholar
Kjos-Hanssen, B. [2003], Local initial segments of the Turing degrees, The Bulletin of Symbolic Logic, vol. 9, pp. 26–36.Google Scholar
Kleene, S. C. and Post, E. L. [1954], The upper semi-lattice of degrees of recursive unsolvability, Annals of Mathematics, vol. 59, no. 2, pp. 379–407.Google Scholar
Lachlan, A. H. [1968], Distributive initial segments of the degrees of unsolvability, Zeitschrift für Mathematische Logik und Grundlagen der Mathematik, vol. 14, pp. 457–472.Google Scholar
Lachlan, A. H. and Lebeuf, R. [1976], Countable initial segments of the degrees of unsolvability, this Journal, vol. 41, pp. 289–300.Google Scholar
Lerman, M. [1971], Initial segments of the degrees of unsolvability, Annals of Mathematics, vol. 93, pp. 365–389.Google Scholar
Lerman, M. [1983], Degrees of unsolvability, Perspectives in Mathematical Logic, Springer-Verlag, Berlin.CrossRefGoogle Scholar
Lubarsky, R. [1987], Lattices of c-degrees, Annals of Pure and Applied Logic, vol. 36, pp. 115–118.Google Scholar
Miller, R. G., Nies, A. O., and Shore, R. A. [2004], The ∀∃-theory of (≤, ∨, ∧) is undecidable, Transactions of the American Mathematical Society, vol. 356, pp. 3025–3067.Google Scholar
Nerode, A. and Shore, R. A. [1980], Second order logic and first order theories of reducibility orderings, The Kleene symposium (Barwise, J., Keisler, H. J., and Kunen, K., editors), North-Holland, Amsterdam, pp. 181–200.Google Scholar
Odifreddi, P. [1983], Forcing and reducibilities, this Journal, vol. 48, pp. 288–310.Google Scholar
Odifreddi, P. [1983a], Forcing and reducibilities IT. forcing in fragments of analysis, this Journal, vol. 48, pp. 724–743.Google Scholar
Sacks, G. E. [1963], Degrees of unsolvability, Annals of Mathematics Studies, vol. 55, Princeton University Press, Princeton, New Jersey.Google Scholar
Sacks, G. E. [1971], Forcing with perfect closed sets, in axiomatic set theory, Proceedings of the symposium on pure mathematics, vol. XII, Part 1, American Mathematical Society, Providence, Rhode Island.Google Scholar
Sacks, G. E. [1972], Review of Thomason 1970, Mathematical Reviews, issue 2, MR0288027 (44 #5225).Google Scholar
Sacks, G. E. [1990], Higher recursion theory, Perspectives in Mathematical Logic, Springer-Verlag, Berlin.Google Scholar
Selivanov, V. L. [1988], Algorithmic complexity of algebraic systems, Matematicheskie Zametki, vol. 44, pp. 823–832 and 863, translation in Mathematical Notes , vol. 44 (1989), pp. 944–950.Google Scholar
Shore, R. A. [1978], On the VB-sentences of a-recursion theory, Generalized recursion theory II (Fenstad, J. E., Gandy, R. O., and Sacks, G. E., editors), Studies in Logic and the Foundations of Mathematics, vol. 94, North-Holland, Amsterdam, pp. 331–354.Google Scholar
Shore, R. A. [1981], The theory ofthe degrees below 0′, Journal of the London Mathematical Society, vol. 24, no. 3, pp. 1–14.CrossRefGoogle Scholar
Shore, R. A. [2007], Local definitions in degree structures: the Turing jump, hyperdegrees and beyond, The Bulletin of Symbolic Logic, vol. 13, pp. 226–239.Google Scholar
Shore, R. A. [2008], Rigidity and biinterpretability in the hyperdegrees, Computational prospects of infinity, Part II: Presented talks (Chong, C. T., Qi, F., and Yang, Y., editors), Lecture Notes Series, vol. 15, World Scientific Publishing Co., Institute for Mathematical Sciences, National University of Singapore, Singapore.Google Scholar
Simpson, M. F. [1985], Arithmetic degrees: Initial segments, ω-REA operators and the ω-jump, Ph.D. thesis, Cornell University.Google Scholar
Spector, C. [1956], On degrees of recursive unsohability, Annals of Mathematics (2), vol. 64, pp. 581–592.Google Scholar
Thomason, S. K. [1967], The forcing method and the upper semilattice of hyperdegrees, Transactions of the American Mathematical Society, vol. 129, pp. 38–57.Google Scholar
Thomason, S. K. [1969], A note on non-distributive sublattices of degrees and hyperdegrees, Canadian Journal of Mathematics, vol. 21, pp. 147–148.Google Scholar
Thomason, S. K. [1970], On initial segments of hyperdegrees, this Journal, vol. 35, pp. 189–197.Google Scholar