Hostname: page-component-7bb8b95d7b-pwrkn Total loading time: 0 Render date: 2024-09-25T18:23:19.459Z Has data issue: false hasContentIssue false
  • English
  • Français

Indescribable cardinals and elementary embeddings

Published online by Cambridge University Press:  12 March 2014

Kai Hauser
Kai Hauser*
Affiliation:
Sloan Laboratory, California Institute of Technology, Pasadena, California 91125
Get access Rights & Permissions [Opens in a new window]

Extract

Indescribability is closely related to the reflection principles of Zermelo-Fränkel set theory. In this axiomatic setting the universe of all sets stratifies into a natural cumulative hierarchy (Vα: α ϵ On) such that any formula of the language for set theory that holds in the universe already holds in the restricted universe of all sets obtained by some stage.

The axioms of ZF prove the existence of many ordinals α such that this reflection scheme holds in the world Vα. Hanf and Scott noticed that one arrives at a large cardinal notion if the reflecting formulas are allowed to contain second order free variables to which one assigns subsets of Vα. For a given collection Ω of formulas in the ϵ language of set theory with higher type variables and a unary predicate symbol they define an ordinal α to be Ω indescribable if for all sentences Φ in Ω and A ⊆ Vα

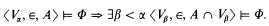
Since a sufficient coding apparatus is available, this definition is (for the classes of formulas that we are going to consider) equivalent to the one that one obtains by allowing finite sequences of relations over Vα, some of which are possibly k-ary. We will be interested mainly in certain standardized classes of formulas: Let 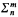(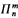, respectively) denote the class of all formulas in the language introduced above whose prenex normal form has n alternating blocks of quantifiers of type m (i.e. (m + 1)th order) starting with ∃ (∀, respectively) and no quantifiers of type greater than m. In Hanf and Scott [1961] it is shown that in ZFC, 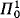indescribability is equivalent to inaccessibility and 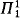indescribability coincides with weak compactness.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 56 , Issue 2 , June 1991 , pp. 439 - 457
Copyright
Copyright © Association for Symbolic Logic 1991

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Dodd, A. J. [1982], The core model, London Mathematical Society Lecture Note Series, vol. 61, Cambridge University Press, Cambridge.CrossRefGoogle Scholar
Drake, F. R. [1974], Set theory, North-Holland, Amsterdam.Google Scholar
Hanf, W. P. and Scott, D. [1961], Classifying inaccessible cardinals, Notices of the American Mathematical Society, vol. 8, p. 445.Google Scholar
Hauser, K. [1989], Independence results for indescribable cardinals, Ph. D. thesis, California Institute of Technology, Pasadena, California.Google Scholar
Jensen, R. B. [1967], Unpublished lectures at Bonn and at Oberwolfach.Google Scholar
Kunen, K. [1971], On the GCH at measurable cardinals, Logic colloquium '69 (Gandy, K. O. and Yates, C. E. M., editors), North-Holland, Amsterdam, pp. 107–110.CrossRefGoogle Scholar
Kunen, K. [1980], Set theory, North-Holland, Amsterdam.Google Scholar
Levy, A. [1971], The sizes of the indescribable cardinals, Axiomatic set theory (Scott, D. S., editor), Proceedings of Symposia in Pure Mathematics, vol. 13, part 1, American Mathematical Society, Providence, Rhode Island, pp. 205–218.CrossRefGoogle Scholar
Martin, D. A. and Steel, J. R. [1988], Projective determinacy, Proceedings of the National Academy of Sciences of the United States of America, vol. 85, pp. 6587–6591.Google ScholarPubMed
Mitchell, W. J. [1979], Hypermeasurable cardinals, Logic colloquium '78 (Boffa, M.et al., editors), North-Holland, Amsterdam, pp. 303–316.Google Scholar
Moschovakis, Y. N. [1976], Indescribable cardinals in L, this Journal, vol. 41, pp. 554–555.Google Scholar
Silver, J. [1971], Unpublished notes on reverse Easton forcing.Google Scholar
Solovay, R. M. and Tennenbaum, S. [1971], Iterated Cohen extensions and Souslin's problem, Annals of Mathematics, ser. 2, vol. 94, pp. 201–245.CrossRefGoogle Scholar
Vaught, R. L. [1963], Indescribable cardinals, Notices of the American Mathematical Society, vol. 10, p. 126.Google Scholar