No CrossRef data available.
Article contents
A generalization of Sierpiński's paradoxical decompositions: Coloring semialgebraic grids
Published online by Cambridge University Press: 12 March 2014
Abstract
A structure 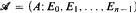 is an n-grid if each Ei, is an equivalence relation on A and whenever X and Y are equivalence classes of, respectively, distinct Ei, and Ej, then X ∩ Y is finite. A coloring χ: A → n is acceptable if whenever X is an equivalence class of Ei, then {x ∈ X: χ(x) = i} is finite. If B is any set, then the n-cube Bn = (Bn; E0, …, En−1) is considered as an n-grid, where the equivalence classes of Ei are the lines parallel to the i-th coordinate axis. Kuratowski [9], generalizing the n = 3 case proved by Sierpihski [17], proved that ℝn has an acceptable coloring iff 2ℵ0 ≤ ℵn−2. The main result is: if
is an n-grid if each Ei, is an equivalence relation on A and whenever X and Y are equivalence classes of, respectively, distinct Ei, and Ej, then X ∩ Y is finite. A coloring χ: A → n is acceptable if whenever X is an equivalence class of Ei, then {x ∈ X: χ(x) = i} is finite. If B is any set, then the n-cube Bn = (Bn; E0, …, En−1) is considered as an n-grid, where the equivalence classes of Ei are the lines parallel to the i-th coordinate axis. Kuratowski [9], generalizing the n = 3 case proved by Sierpihski [17], proved that ℝn has an acceptable coloring iff 2ℵ0 ≤ ℵn−2. The main result is: if 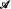 is a semialgebraic (i.e., first-order definable in the field of reals) n-grid, then the following are equivalent: (1) if
is a semialgebraic (i.e., first-order definable in the field of reals) n-grid, then the following are equivalent: (1) if 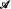 embeds all finite n-cubes, then 2ℵ0 ≤ ℵn−2: (2) if
embeds all finite n-cubes, then 2ℵ0 ≤ ℵn−2: (2) if 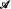 embeds ℝn, then 2ℵ0 ≤ ℵn−2; (3)
embeds ℝn, then 2ℵ0 ≤ ℵn−2; (3) 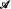 has an acceptable coloring.
has an acceptable coloring.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 2012


