Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Andrews, Peter B.
1974.
Provability in Elementary Type Theory.
Mathematical Logic Quarterly,
Vol. 20,
Issue. 25-27,
p.
411.
Hintikka, Jaakko
and
Carlson, Lauri
1978.
Formal Semantics and Pragmatics for Natural Languages.
p.
1.
Dummett, Michael
1979.
Meaning and Use.
p.
123.
Hintikka, Jaakko
1981.
Tome 1 Philosophie du langage, Logique philosophique / Volume 1 Philosophy of language, Philosophical logic.
p.
57.
Hintikka, Jaakko
1986.
Extremality Assumptions in the Foundations of Mathematics.
PSA: Proceedings of the Biennial Meeting of the Philosophy of Science Association,
Vol. 1986,
Issue. 2,
p.
247.
Bai, Mino
and
Blair, Howard A.
1992.
Logic Programming and Automated Reasoning.
Vol. 624,
Issue. ,
p.
320.
Miller, Dale
1992.
Unification under a mixed prefix.
Journal of Symbolic Computation,
Vol. 14,
Issue. 4,
p.
321.
Wolfram, D.A.
1994.
A semantics for λProlog.
Theoretical Computer Science,
Vol. 136,
Issue. 1,
p.
277.
Hintikka, Jaakko
1995.
From Dedekind to Gödel.
p.
21.
Andrews, Peter B.
2001.
Handbook of Automated Reasoning.
p.
965.
Benzmüller, Christoph E.
and
Brown, Chad E.
2005.
Theorem Proving in Higher Order Logics.
Vol. 3603,
Issue. ,
p.
66.
Benzmüller, Christoph E.
Brown, Chad E.
and
Kohlhase, Michael
2006.
Automated Reasoning.
Vol. 4130,
Issue. ,
p.
220.
Muskens, Reinhard
2007.
Handbook of Modal Logic.
Vol. 3,
Issue. ,
p.
621.
Benzmueller, Christoph
Brown, Chad E.
and
Kohlhase, Michael
2009.
Cut-Simulation and Impredicativity.
Logical Methods in Computer Science,
Vol. Volume 5, Issue 1,
Issue. ,
Benzmüller, Christoph
2009.
Emerging Challenges for Security, Privacy and Trust.
Vol. 297,
Issue. ,
p.
387.
Backes, Julian
and
Brown, Chad E.
2010.
Automated Reasoning.
Vol. 6173,
Issue. ,
p.
76.
Gentilini, Paolo
and
Martelli, Maurizio
2010.
Abstract deduction and inferential models for type theory.
Information and Computation,
Vol. 208,
Issue. 7,
p.
737.
Benzmueller, C.
and
Paulson, L. C.
2010.
Multimodal and intuitionistic logics in simple type theory.
Logic Journal of IGPL,
Vol. 18,
Issue. 6,
p.
881.
Brown, Chad E.
and
Smolka, Gert
2010.
Analytic Tableaux for Simple Type Theory and its First-Order Fragment.
Logical Methods in Computer Science,
Vol. Volume 6, Issue 2,
Issue. ,
Benzmüller, Christoph
2010.
Verification, Induction, Termination Analysis.
Vol. 6463,
Issue. ,
p.
117.
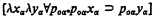 , i.e., xα = yα iff every set which contains xα also contains yα. However, in a nonstandard model of type theory, the sets may be so sparse that the wff above does not denote the true equality relation. We shall use this observation to construct a general model in the sense of [2] in which the Axiom of Extensionality is not valid. Thus Theorem 2 of [2] is technically incorrect. However, it is easy to remedy the situation by slightly modifying the definition of general model.
, i.e., xα = yα iff every set which contains xα also contains yα. However, in a nonstandard model of type theory, the sets may be so sparse that the wff above does not denote the true equality relation. We shall use this observation to construct a general model in the sense of [2] in which the Axiom of Extensionality is not valid. Thus Theorem 2 of [2] is technically incorrect. However, it is easy to remedy the situation by slightly modifying the definition of general model.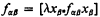 as an axiom schema.
as an axiom schema.

