It has been shown that, for all rational numbers r such that 0≤ r ≤ 1, the ℵ0-valued Łukasiewicz propositional calculus whose designated truth-values are those truth-values x such that r ≤ x ≤ 1 may be formalised completely by means of finitely many axiom schemes and primitive rules of procedure. We shall consider now the case where r is rational, 0≥r≤1 and the designated truth-values are those truth-values x such that r≤x≤1.

We note that, in the subcase of the previous case where r = 1, a complete formalisation is given by the following four axiom schemes together with the rule of modus ponens (with respect to C),

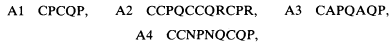
the functor A being defined in the usual way. The functors B, K, L will also be considered to be defined in the usual way. Let us consider now the functor Dαβ such that if P, Dαβ take the truth-values x, dαβ(x) respectively, α, β are relatively prime integers and r = α/β then

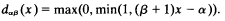
It follows at once from a theorem of McNaughton that the functor Dαβ is definable in terms of C and N in an effective way. If r = 0 we make the definition

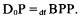
We note first that if x ≤ α/β then dαβ(x)≤(β + 1)α/β − α = α/β. Hence

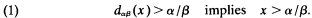
Let us now define the functions dnαβ(x) (n = 0,1,…) by

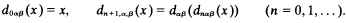
Since

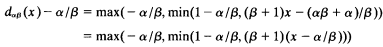
it follows easily that

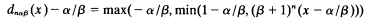
and that

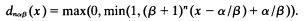
Thus, if x is designated, x − α/β > 0 and, if n > − log(x − α/β)/log(β + 1), then (β + 1)n(x−α/β) > 1.