Article contents
A fixed point for the jump operator on structures
Published online by Cambridge University Press: 12 March 2014
Abstract
Assuming that 0# exists, we prove that there is a structure that can effectively interpret its own jump. In particular, we get a structure 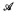 such that
such that
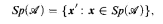
where  is the set of Turing degrees which compute a copy of
is the set of Turing degrees which compute a copy of 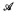
More interesting than the result itself is its unexpected complexity. We prove that higher-order arithmetic, which is the union of full “nth-order arithmetic for all n, cannot prove the existence of such a structure.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 2013
References
REFERENCES
- 5
- Cited by


