Article contents
Fine structure for tame inner models
Published online by Cambridge University Press: 12 March 2014
Extract
In this paper, we solve the strong uniqueness problem posed in [St2]. That is, we extend the full fine structure theory of [MiSt] to backgrounded 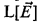 models all of whose levels are tame (defined in [St2] and below). As a consequence, more powerful large cardinal properties reflect to fine structural inner models. For example, we get the following extension to [MiSt, Theorem 11.3] and [St2, Theorem 0.3].
models all of whose levels are tame (defined in [St2] and below). As a consequence, more powerful large cardinal properties reflect to fine structural inner models. For example, we get the following extension to [MiSt, Theorem 11.3] and [St2, Theorem 0.3].
Suppose that there is a strong cardinal that is a limit of Woodin cardinals. Then there is a good extender sequence 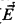 such that
such that
(1) every level of 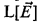 is a sound, tame mouse, and
is a sound, tame mouse, and
(2) 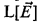 ⊨ “There is a strong cardinal that is a limit of Woodin cardinals”.
⊨ “There is a strong cardinal that is a limit of Woodin cardinals”.
Recall that 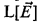 satisfies GCH if all its levels are sound. Another consequence of our work is the following covering property, an extension to [St1, Theorem 1.4] and [St3, Theorem 1.10].
satisfies GCH if all its levels are sound. Another consequence of our work is the following covering property, an extension to [St1, Theorem 1.4] and [St3, Theorem 1.10].
Suppose that fi is a normal measure on Ω and that all premice are tame. Then Kc, the background certified core model, exists and is a premouse of height Ω. Moreover, 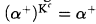 for μ-almost every α < Ω.
for μ-almost every α < Ω.
Ideas similar to those introduced here allow us to extend the fine structure theory of [Sch] to the level of tame mice. The details of this extension shall appear elsewhere. From the extension of [Sch] and Theorem 0.2, new relative consistency results follow. For example, we have the following application.
If there is a cardinal κ such that κ is κ+-strongly compact, then there is a premouse that is not tame.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1996
References
- 13
- Cited by


