Hostname: page-component-8448b6f56d-t5pn6 Total loading time: 0 Render date: 2024-04-19T21:37:11.809Z Has data issue: false hasContentIssue false
  • English
  • Français

Fields interpretable in superrosy groups with NIP (the non-solvable case)

Published online by Cambridge University Press:  12 March 2014

Krzysztof Krupiński
Krzysztof Krupiński*
Affiliation:
Instytut Matematyczny Uniwersytetu Wrocławskiego, Pl. Grunwaldzki 2/4 50-384 Wroclaw, Poland Mathematics Department, University of Illinois at Urbana-Champaign, 1409 W. Green Street, Urbana, IL 61801, USA, E-mail: kkrup@math.uni.wroc.pl
Get access Rights & Permissions [Opens in a new window]

Abstract

Let G be a group definable in a monster model 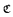of a rosy theory satisfying NIP. Assume that G has hereditarily finitely satisfiable generics and 1 < Ub(G) < ∞. We prove that if G acts definably on a definable set of Uр-rank 1, then, under some general assumption about this action, there is an infinite field interpretable in 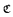. We conclude that if G is not solvable-by-finite and it acts faithfully and definably on a definable set of Uр-rank 1, then there is an infinite field interpretable in 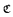. As an immediate consequence, we get that if G has a definable subgroup H such that Uр(G) = Uр(H) + 1 and G/⋂g∈GHg is not solvable-by-finite, then an infinite field interpretable in 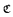also exists.

Keywords

superrosy groupinterpretable fieldnon independence property
Type
Research Article
Information
The Journal of Symbolic Logic , Volume 75 , Issue 1 , March 2010 , pp. 372 - 386
Copyright
Copyright © Association for Symbolic Logic 2010

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1] Adler, H., A geometric introduction to forking and thorn-forking, preprint.Google Scholar
[2] Adler, H., Thorn-forking as local forking, preprint.Google Scholar
[3] Baudisch, A., A new uncountably categorical group, Transactions of the American Mathematical Society, vol. 348 (1996), pp. 3889–3940.Google Scholar
[4] Ealy, C., Krupiński, K., and Pillay, A., Superrosy dependent groups having finitely satisfiable generics, Annals of Pure and Applied Logic, vol. 151 (2008), pp. 1–21.CrossRefGoogle Scholar
[5] Ealy, C. and Onshuus, A., Characterizing rosy theories, this Journal, vol. 72 (2007), pp. 919–940.Google Scholar
[6] Gruenenwald, G. and Haug, F., On stable torsion-free nilpotent groups, Archive for Mathematical Logic, vol. 32 (1993), pp. 451–462.CrossRefGoogle Scholar
[7] Krupiński, K., Fields interpretable in rosy theories, Israel Journal of Mathematics, to appear.Google Scholar
[8] Macpherson, D., Mosley, A., and Tent, K., Permutation groups in o-minimal structures, Journal of the London Mathematical Society, vol. 62 (2000), pp. 650–670.Google Scholar
[9] Onshuus, A., Properties and consequences of thorn-independence, this Journal, vol. 71 (2006), no. 1, pp. 1–21.Google Scholar
[10] Peterzil, Y. and Starchenko, S., Definable homomorphisms of abelian groups in o-minimal structures, Annals of Pure and Applied Logic, vol. 101 (2000), pp. 1–27.Google Scholar
[11] Pillay, A., Geometric stability theory, Clarendon Press, Oxford, 1996.CrossRefGoogle Scholar
[12] Poizat, B., Stable groups, Mathematical Surveys and Monographs, vol. 87, American Mathematical Society, Providence, 2001.Google Scholar
[13] Wagner, F., Simple theories, Kluwer Academic Publishers, Dordrecht, 2000.Google Scholar
[14] Zilber, B., Uncountable categorical nilpotent groups and Lie algebras, Russian Mathematics (Izvestiya Vysshikh Uchebnykh Zavedeniǐ), vol. 26 (1982), pp. 98–99.Google Scholar