Article contents
Fibred semantics and the weaving of logics. Part 1: Modal and intuitionistic logics
Published online by Cambridge University Press: 12 March 2014
Abstract
This is Part 1 of a paper on fibred semantics and combination of logics. It aims to present a methodology for combining arbitrary logical systems Li, i ∈ I, to form a new system LI. The methodology ‘fibres’ the semantics 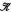 i of Li into a semantics for LI, and ‘weaves’ the proof theory (axiomatics) of Li into a proof system of LI. There are various ways of doing this, we distinguish by different names such as ‘fibring’, ‘dovetailing’ etc, yielding different systems, denoted by
i of Li into a semantics for LI, and ‘weaves’ the proof theory (axiomatics) of Li into a proof system of LI. There are various ways of doing this, we distinguish by different names such as ‘fibring’, ‘dovetailing’ etc, yielding different systems, denoted by 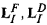 etc. Once the logics are ‘weaved’, further ‘interaction’ axioms can be geometrically motivated and added, and then systematically studied. The methodology is general and is applied to modal and intuitionistic logics as well as to general algebraic logics. We obtain general results on bulk, in the sense that we develop standard combining techniques and refinements which can be applied to any family of initial logics to obtain further combined logics.
etc. Once the logics are ‘weaved’, further ‘interaction’ axioms can be geometrically motivated and added, and then systematically studied. The methodology is general and is applied to modal and intuitionistic logics as well as to general algebraic logics. We obtain general results on bulk, in the sense that we develop standard combining techniques and refinements which can be applied to any family of initial logics to obtain further combined logics.
The main results of this paper is a construction for combining arbitrary, (possibly not normal) modal or intermediate logics, each complete for a class of (not necessarily frame) Kripke models. We show transfer of recursive axiomatisability, decidability and finite model property.
Some results on combining logics (normal modal extensions of K) have recently been introduced by Kracht and Wolter, Goranko and Passy and by Fine and Schurz as well as a multitude of special combined systems existing in the literature of the past 20–30 years. We hope our methodology will help organise the field systematically.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1996
References
REFERENCES
- 49
- Cited by


