Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Gitik, Moti
1993.
On measurable cardinals violating the continuum hypothesis.
Annals of Pure and Applied Logic,
Vol. 63,
Issue. 3,
p.
227.
Jech, Thomas
1995.
Singular Cardinals and the PCF Theory.
Bulletin of Symbolic Logic,
Vol. 1,
Issue. 4,
p.
408.
Gitik, Moti
and
Mitchell, William J.
1996.
Indiscernible sequences for extenders, and the singular cardinal hypothesis.
Annals of Pure and Applied Logic,
Vol. 82,
Issue. 3,
p.
273.
Gitik, Moti
1996.
Blowing up the power of a singular cardinal.
Annals of Pure and Applied Logic,
Vol. 80,
Issue. 1,
p.
17.
Gitik, Moti
and
Shelah, Saharon
1998.
On densities of box products.
Topology and its Applications,
Vol. 88,
Issue. 3,
p.
219.
Gitik, Moti
2002.
Blowing up power of a singular cardinal—wider gaps.
Annals of Pure and Applied Logic,
Vol. 116,
Issue. 1-3,
p.
1.
Gitik, Moti
and
Sharon, Assaf
2007.
On SCH and the approachability property.
Proceedings of the American Mathematical Society,
Vol. 136,
Issue. 1,
p.
311.
NEEMAN, ITAY
2009.
ARONSZAJN TREES AND FAILURE OF THE SINGULAR CARDINAL HYPOTHESIS.
Journal of Mathematical Logic,
Vol. 09,
Issue. 01,
p.
139.
Gitik, Moti
2010.
Handbook of Set Theory.
p.
1351.
Honzik, Radek
2010.
Global singularization and the failure of SCH.
Annals of Pure and Applied Logic,
Vol. 161,
Issue. 7,
p.
895.
Gitik, Moti
and
Golshani, Mohammad
2014.
Adding a lot of Cohen reals by adding a few. I.
Transactions of the American Mathematical Society,
Vol. 367,
Issue. 1,
p.
209.
Sinapova, Dima
and
Unger, Spencer
2015.
Scales at $${N_\omega }$$.
Israel Journal of Mathematics,
Vol. 209,
Issue. 1,
p.
463.
Cummings, James
Friedman, Sy-David
Magidor, Menachem
Rinot, Assaf
and
Sinapova, Dima
2018.
Ordinal definable subsets of singular cardinals.
Israel Journal of Mathematics,
Vol. 226,
Issue. 2,
p.
781.
Gitik, Moti
2020.
Extender-based forcings with overlapping extenders and negations of the Shelah Weak Hypothesis.
Journal of Mathematical Logic,
Vol. 20,
Issue. 03,
p.
2050013.
Poveda, Alejandro
Rinot, Assaf
and
Sinapova, Dima
2021.
Sigma-Prikry forcing I: The Axioms.
Canadian Journal of Mathematics,
Vol. 73,
Issue. 5,
p.
1205.
Gitik, Moti
2021.
Another method for constructing models of not approachability and not SCH.
Archive for Mathematical Logic,
Vol. 60,
Issue. 3-4,
p.
469.
Poveda, Alejandro
Rinot, Assaf
and
Sinapova, Dima
2022.
Sigma-Prikry forcing II: Iteration Scheme.
Journal of Mathematical Logic,
Vol. 22,
Issue. 03,
Jirattikansakul, Sittinon
2023.
Blowing up the power of a singular cardinal of uncountable cofinality with collapses.
Annals of Pure and Applied Logic,
Vol. 174,
Issue. 6,
p.
103257.
Poveda, Alejandro
Rinot, Assaf
and
Sinapova, Dima
2023.
Sigma-Prikry forcing III: Down to ℵ.
Advances in Mathematics,
Vol. 435,
Issue. ,
p.
109377.
BENHAMOU, TOM
and
GITIK, MOTI
2024.
ON COHEN AND PRIKRY FORCING NOTIONS.
The Journal of Symbolic Logic,
Vol. 89,
Issue. 2,
p.
858.
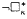 ”. In §4 a variation of the forcing of [The SCH revisited, §1] is defined. It behaves nicely in iteration processes. As an application, we sketch a construction of a model satisfying:
”. In §4 a variation of the forcing of [The SCH revisited, §1] is defined. It behaves nicely in iteration processes. As an application, we sketch a construction of a model satisfying:

