Article contents
Describing ordinals using functionals of transfinite type
Published online by Cambridge University Press: 12 March 2014
Extract
Bachmann, in [2] shows how certain ordinals <Ω(Ω = Ω1 where Ωξ is the (1 + ξ)th infinite initial ordinal) may be described from below using suitable descriptions of ordinals <Ω2. The aim of this paper is to consider another approach to describing ordinal <Ω and compare it with the Bachmann method. Our approach will use functionals of transfinite type based on Ω.
The Bachmann method consists in denning a hierarchy 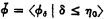 of normal functions ϕδ: Ω → Ω (i.e. continuous and strictly increasing) for δ ≤ η0 < Ω2, starting with ϕ0(λ) = ω1 + λ. The definition of
of normal functions ϕδ: Ω → Ω (i.e. continuous and strictly increasing) for δ ≤ η0 < Ω2, starting with ϕ0(λ) = ω1 + λ. The definition of 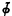 depends on a suitable description of the ordinals ≤ η0. This is obtained by defining a hierarchy 〈Fδ ∣ δ ≤ Ω2〉 of normal functions Fδ: Ω2 → Ω2 analogously to the definition of the initial segment 〈ϕδ ∣ δ ≤ Ω〉 of
depends on a suitable description of the ordinals ≤ η0. This is obtained by defining a hierarchy 〈Fδ ∣ δ ≤ Ω2〉 of normal functions Fδ: Ω2 → Ω2 analogously to the definition of the initial segment 〈ϕδ ∣ δ ≤ Ω〉 of 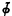 . The ordinal η0 is
. The ordinal η0 is 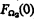 .
.
Note. Our description of Bachmann's hierarchies will differ slightly from those in Bachmann's paper. Let 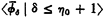 and
and 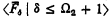 denote the hierarchies in [2]. Then as Bachmann's normal functions are not defined at 0 we let
denote the hierarchies in [2]. Then as Bachmann's normal functions are not defined at 0 we let 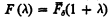 for λ, δ < Ω2. Bachmann defines
for λ, δ < Ω2. Bachmann defines 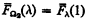 for 0 < λ < Ω2 but it seems more natural to omit this so that we let
for 0 < λ < Ω2 but it seems more natural to omit this so that we let 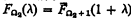 . The situation is analogous for
. The situation is analogous for 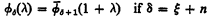 and leads to the following definitions:
and leads to the following definitions:
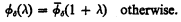
where n < ω and ξ is a limit number of cofinality Ω, and
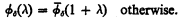
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1972
References
REFERENCES
- 9
- Cited by


