Hostname: page-component-8448b6f56d-jr42d Total loading time: 0 Render date: 2024-04-24T13:00:09.286Z Has data issue: false hasContentIssue false
  • English
  • Français

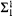-definability at uncountable regular cardinals

Published online by Cambridge University Press:  12 March 2014

Philipp Lücke
Philipp Lücke*
Affiliation:
Institut für Mathematische Logik und Grundlagenforschung, Fachbereich Mathematik und Informatik, Universität Münster, Einsteinstr. 62, 48149 Münster, Germany, E-mail: philipp.luecke@uni-muenster.de
Get access Rights & Permissions [Opens in a new window]

Abstract

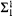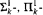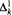Let κ be an infinite cardinal. A subset of (κκ)n is a -subset if it is the projection p[T] of all cofinal branches through a subtree T of (>κκ)n+1 of height κ. We define and -subsets of (κκ)n as usual.

Given an uncountable regular cardinal κ with κ = κ<κ and an arbitrary subset A of κκ, we show that there is a <κ-closed forcing ℙ that satisfies the κ+-chain condition and forces A to be a 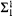-subset of κκ in every ℙ-generic extension of V. We give some applications of this result and the methods used in its proof.

(i) Given any set x, we produce a partial order with the above properties that forces x to be an element of L.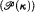

(ii) We show that there is a partial order with the above properties forcing the existence of a well-ordering of κκ whose graph is a -subset of κκ × κκ.

(iii) We provide a short proof of a result due to Mekler and Väänänen by using the above forcing to add a tree T of cardinality and height κ such that T has no cofinal branches and every tree from the ground model of cardinality and height κ without a cofinal branch quasi-order embeds into T.

(iv) We will show that generic absoluteness for 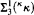-formulae (i.e., formulae with parameters which define -subsets of κκ) under <κ-closed forcings that satisfy the κ+-chain condition is inconsistent.

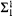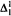In another direction, we use methods from the proofs of the above results to show that - and -subsets have some useful structural properties in certain ZFC-models.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 77 , Issue 3 , September 2012 , pp. 1011 - 1046
Copyright
Copyright © Association for Symbolic Logic 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1] Asperó, David and Friedman, Sy-David, Large cardinals and locally defined well-orders of the universe, Annals of Pure and Applied Logic, vol. 157 (2009), no. 1, pp. 1–15.Google Scholar
[2] Asperó, David and Friedman, Sy-David, Definable wellorderings of Hω2 and CH, Preprint available online at http://www.logic.univie.ac.at/~sdf/papers/joint.aspero.omega-2.pdf.Google Scholar
[3] Bagaria, Joan and Friedman, Sy D., Generic absoluteness, Proceedings of the XIth Latin American Symposium on Mathematical Logic (Mérida, 1998), vol. 108, 2001, pp. 3–13.Google Scholar
[4] Cummings, James, Iterated forcing and elementary embeddings, The handbook of set theory (Foreman, M., Kanamorie, A., and Magidor, M., editors), vol. 2, Springer, Berlin, 2010, pp. 775–884.CrossRefGoogle Scholar
[5] Feng, Qi, Magidor, Menachem, and Woodin, Hugh, Universally Baire sets of reals, Set theory of the continuum (Berkeley, CA, 1989), Mathematical Sciences Research Institute Publications, vol. 26, Springer, New York, 1992, pp. 203–242.CrossRefGoogle Scholar
[6] Friedman, Sy-David, Forcing, combinatorics and definability, Proceedings of the 2009 RIMS Workshop on Combinatorical Set Theory and Forcing Theory in Kyoto, Japan, RIMS Kokyuroku No. 1686, 2010, pp. 24–40.Google Scholar
[7] Friedman, Sy-David and Holy, Peter, Condensation and large cardinals, Fundamenta Mathematical vol. 215 (2011), no. 2, pp. 133–166.CrossRefGoogle Scholar
[8] Friedman, Sy-David, Hyttinen, Tapani, and Kulikov, Vadim, Generalised descriptive set theory and classification theory, Preprint available online at http://www.logic.univie.ac.at/~sdf/papers/joint.tapani.vadim.pdf.Google Scholar
[9] Fuchs, Gunter, Closed maximality principles: implications, separations and combinations, this Journal, vol. 73 (2008), no. 1, pp. 276–308.Google Scholar
[10] Harrington, Leo, Long projective wellorderings, Annals of Pure andApplied Logic, vol. 12 (1977), no. 1, pp. 1–24.Google Scholar
[11] Hyttinen, Tapani and Rautila, Mika, The canary tree revisited, this Journal, vol. 66 (2001), no. 4, pp. 1677–1694.Google Scholar
[12] Hyttinen, Tapani and Väänänen, Jouko, On Scott and Karp trees of uncountable models, this Journal, vol. 55 (1990), no. 3, pp. 897–908.Google Scholar
[13] Jech, Thomas J., Trees, this Journal, vol. 36 (1971), pp. 1–14.Google Scholar
[14] Jensen, R. B. and Solovay, R. M., Some applications of almost disjoint sets, Mathematical Logic and Foundations of Set Theory, North-Holland, Amsterdam, 1970, pp. 84–104.Google Scholar
[15] Kanamori, Akihiro, The higher infinite, second ed., Springer Monographs in Mathematics, Springer-Verlag, Berlin, 2003.Google Scholar
[16] Laver, Richard, Certain very large cardinals are not created in small forcing extensions, Annals of Pure and Applied Logic, vol. 149 (2007), no. 1–3, pp. 1–6.Google Scholar
[17] Mekler, Alan and Väänänen, Jouko, Trees and -subsets of ω1 ω1 , this Journal, vol. 58 (1993), no. 3, pp. 1052–1070.Google Scholar
[18] Nadel, Mark and Stavi, Jonathan, L∞λ,-equivalence, isomorphism and potential isomorphism, Transactions of the American Mathematical Society, vol. 236 (1978), pp. 51–74.Google Scholar
[19] Neeman, Itay and Zapletal, Jindřich, Proper forcings and absoluteness in L(R), Commentationes Mathematicae Universitatis Carolinae, vol. 39 (1998), no. 2, pp. 281–301.Google Scholar
[20] Shelah, Saharon and Väisänen, Pauli, The number of L∞k-equivalent nonisomorphic models for k weakly compact, Fundamenta Mathematicae, vol. 174 (2002), no. 2, pp. 97–126.Google Scholar
[21] Todorčević, Stevo and Väänänen, Jouko, Trees and Ehrenfeucht-Fraïssé games, Annals of Pure and Applied Logic, vol. 100 (1999), no. 1–3, pp. 69–97.Google Scholar
[22] Väänänen, Jouko, A Cantor-Bendixson theorem for the space , Polska Akademia Nauk. Fundamenta Mathematical vol. 137 (1991), no. 3, pp. 187–199.Google Scholar
[23] Väänänen, Jouko, Games and trees in infinitary logic: A survey, Quantifiers (Krynicki, M., Mostowski, M., and Szczerba, L., editors), Kluwer Academic Publishers, 1995, pp. 105–138.Google Scholar