Hostname: page-component-76fb5796d-qxdb6 Total loading time: 0 Render date: 2024-04-26T09:25:14.859Z Has data issue: false hasContentIssue false
  • English
  • Français

Definability and decidability issues in extensions of the integers with the divisibility predicate

Published online by Cambridge University Press:  12 March 2014

Patrick Cegielski ,
Yuri Matiyasevich  and
Denis Richard
Patrick Cegielski
Affiliation:
L.I.T.P., I.B.P., U.R.A. 248, Université Paris XII, I.U.T de Fontainebleau, Route Hurtault, F-77300 Fontainebleau, France, E-mail: cep@litp.ibp.fr
Yuri Matiyasevich
Affiliation:
Steklov Institute of Mathematics, 27 Fontanka, Saint-Petersbourg, 191011, Russie, E-mail: yumat@pomi.ras.ru
Denis Richard
Affiliation:
Laboratoire de Logique, Algorithmique, et Informatique de Clermont i (LLAIC 1), I.U.T. Informatique, B.P. 86, F-63172 Aubière Cedex, France, E-mail: richard@llaic.univ-bpclermont.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 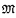be a first-order structure; we denote by DEF(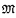) the set of all first-order definable relations and functions within 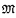. Let π be any one-to-one function from ℕ into the set of prime integers.

Let ∣ and • be respectively the divisibility relation and multiplication as function. We show that the sets DEF(ℕ, π, ∣) and DEF(ℕ, π, •) are equal. However there exists function π such that the set DEF(ℕ, +, ∣), or, equivalently, DEF(ℕ, π, •) is not equal to DEF(ℕ, +, •). Nevertheless, in all cases there is an {π, •}-definable and hence also {π, |}-definable structure over π which is isomorphic to 〈ℕ, +, •〉. Hence theories TH(ℕ, π, ∣) and TH(ℕ, π, •) are undecidable.

The binary relation of equipotence between two positive integers saying that they have equal number of prime divisors is not definable within the divisibility lattice over positive integers. We prove it first by comparing the lower bound of the computational complexity of the additive theory of positive integers and of the upper bound of the computational complexity of the theory of the mentioned lattice.

The last section provides a self-contained alternative proof of this latter result based on a decision method linked to an elimination of quantifiers via specific tables.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 61 , Issue 2 , June 1996 , pp. 515 - 540
Copyright
Copyright © Association for Symbolic Logic 1996

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Balcázar, José Luis, Díaz, Josep, and Gabarró, Joaquim, Structural complexity, Springer-Verlag, Berlin, 1988.Google Scholar
[2]Beth, Evert Willem, On Padoa's method in the theory of definition, Koningklijke Nederlandse Akademie van wetenschappen, Proceedings of the section of sciences, series A, Mathematical sciences, no. 56, 1953, pp. 330–339; also Indagationes mathematicae, vol. 15, pp. 330–339.Google Scholar
[3]Cegielski, Patrick, La théorie élémentaire de la multiplication, Model theory and arithmetic (Berline, , McAloon, , Ressayre, , editors), Lecture Notes in Mathematics, Number 890, Springer-Verlag, pp. 44–89.Google Scholar
[4]Cegielski, Patrick, La théorie élémentaire de la divisibilité est finiment axiomatisable, Comptes Rendus de l'Académie des Sciences, Paris t. 299, vol. I (1984), pp. 367–369.Google Scholar
[5]Cegielski, Patrick, The Elementary Theory of the natural Lattice is Finitely Axiomatizable, Notre Dame Journal of Formal Logic, vol. 30 (1989), pp. 138–150.Google Scholar
[6]Cegielski, Patrick, Definability, decidability and complexity, to appear in Mathematics and Computer Science, (Nivat, Maurice and Grigorieff, Serge, editors), Annals of Mathematics on Artificial Intelligence, Baltzer, Suisse, 1996.Google Scholar
[7]Cegielski, Patrick, and Richard, Denis, Indécidabilité de la théorie des entiers naturels munis d'une énumération des premiers et de la divisibilité, Comptes Rendus de l'Académie des Scinces, Paris t. 315, vol. I (1992), pp. 1431–1434.Google Scholar
[8]Compton, Kevin J. and Henson, C. Ward, A uniform method for proving lower bounds on the computational complexity of logical theories, Annals of Pure and Applied Logic, vol. 48 (1990), pp. 1–79.Google Scholar
[9]Ebbinghaus, H. D., Flum, J., and Thomas, W., Mathematical Logic, Springer-Verlag, Berlin, 1984.Google Scholar
[10]Erdös, Paul, How many pairs of products of consecutive integers have the same prime factors?, American Mathematical Monthly, vol. 87 (1980), pp. 391–392.Google Scholar
[11]Goodstein, Reuben Louis, Hilbert's Tenth Problem and the independence of recursive difference, The Journal of the London Mathematical Society (Second Series), vol. 10, no. 2, pp. 175–176.Google Scholar
[12]Langevin, Michel, Approximations diophantiennes et nombres transcendants, Luminy 1990 (Philippon, Patrice, editor), de Gruyter, Berlin, 1992, pp. 203–214.Google Scholar
[13]Mendelson, Elliott, Introduction to mathematical logic, Van Nostrand, 1964; 2nd edition, 1979; 3rd edition, Wadsworth, California, 1987.Google Scholar
[14]Michel, Pascal, Borne supérieure de la complexité de la théorie de ℕ muni de la relation de divisibilité, Model Theory and Arithmetic (Berline, , McAloon, , and Ressayre, , editors), Lecture Notes in Mathematics, Number 890, Springer-Verlag, Berlin, 1981, pp. 242–250.Google Scholar
[15]More, Malika, Images de spectres binaires par des polynômes, Comptes Rendus de l'Académie des Sciences, Paris, t. 315, vol. I (1992), pp. 343–348.Google Scholar
[16]Padoa, Alessandro, Essai d'une théorie algébrique des nombres entiers, précédé d'une introduction logique à une théorie deductive quelconque, Bibliothèque du Congrès international de philosophie, Paris, 1900, vol. 3, Armand Colin, 1901, pp. 309–365; partial English translation in van Heijenoort, From Frege to Gödei, Harvard University Press, 1967, pp. 118–123.Google Scholar
[17]Poizat, Bruno, Cours de théorie des modèles, Offilib, Paris, 1985.Google Scholar
[18]Richard, Denis, first publication in [19] and [22].Google Scholar
[19]Poizat, Bruno, Définissabilité en arithmétique et méthode de codage Z.B.V. appliquée à des langages avec successeurs et coprimarité, Thèse de doctorat d'État, Université de Lyon-I, 1985.Google Scholar
[20]Poizat, Bruno, Answer to a problem raised by J. Robinson: the arithmetic of positive or negative integers is definable from successor and divisibility, this Journal, vol. 50 (1985), pp. 927–935.Google Scholar
[21]Poizat, Bruno, All arithmetical sets ofpowers ofprimes are first-order definable in terms of the successor function and the coprimeness predicate, Discrete Mathematics, vol. 53 (1985), pp. 221–247.Google Scholar
[22]Poizat, Bruno, Equivalence of some questions in mathematical logic with some conjectures in number theory, Number Theory and Applications, (Mollin, , editor), NATO Asi Series, Series C: Mathematical and Physical Sciences, vol. 265 (1988), pp. 529–545.Google Scholar
[23]Robinson, Julia, Definability and decision problems in arithmetic, this Journal, vol. 14 (1949), pp. 98–114.Google Scholar
[24]Svenonius, Lars, A theorem on permutations in models, Theoria, vol. 25 (1959), pp. 173–178.Google Scholar
[25]Woods, Alan, Some problems in logic and number theory and their connections, Thesis, University of Manchester, 1981.Google Scholar
[26]Younger, D. H., Recognition and parsing of context-free languages in time n 3, Information and Control, vol. 10 (1967), pp. 189–208.Google Scholar