Article contents
Computability of Fraïssé limits
Published online by Cambridge University Press: 12 March 2014
Abstract
Fraïssé studied countable structures 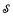 through analysis of the age of
through analysis of the age of 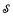 , i.e., the set of all finitely generated substructures of
, i.e., the set of all finitely generated substructures of 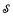 . We investigate the effectiveness of his analysis, considering effectively presented lists of finitely generated structures and asking when such a list is the age of a computable structure. We focus particularly on the Fraïssé limit. We also show that degree spectra of relations on a sufficiently nice Fraïssé limit are always upward closed unless the relation is definable by a quantifier-free formula. We give some sufficient or necessary conditions for a Fraïssé limit to be spectrally universal. As an application, we prove that the computable atomless Boolean algebra is spectrally universal.
. We investigate the effectiveness of his analysis, considering effectively presented lists of finitely generated structures and asking when such a list is the age of a computable structure. We focus particularly on the Fraïssé limit. We also show that degree spectra of relations on a sufficiently nice Fraïssé limit are always upward closed unless the relation is definable by a quantifier-free formula. We give some sufficient or necessary conditions for a Fraïssé limit to be spectrally universal. As an application, we prove that the computable atomless Boolean algebra is spectrally universal.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 2011
References
REFERENCES
- 10
- Cited by


