Article contents
AUTOMORPHISM GROUPS OF COUNTABLE ARITHMETICALLY SATURATED MODELS OF PEANO ARITHMETIC
Published online by Cambridge University Press: 22 December 2015
Abstract
If 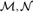 ${\cal M},{\cal N}$ are countable, arithmetically saturated models of Peano Arithmetic and
${\cal M},{\cal N}$ are countable, arithmetically saturated models of Peano Arithmetic and 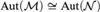 ${\rm{Aut}}\left( {\cal M} \right) \cong {\rm{Aut}}\left( {\cal N} \right)$, then the Turing-jumps of
${\rm{Aut}}\left( {\cal M} \right) \cong {\rm{Aut}}\left( {\cal N} \right)$, then the Turing-jumps of  ${\rm{Th}}\left( {\cal M} \right)$ and
${\rm{Th}}\left( {\cal M} \right)$ and 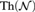 ${\rm{Th}}\left( {\cal N} \right)$ are recursively equivalent.
${\rm{Th}}\left( {\cal N} \right)$ are recursively equivalent.
- Type
- Articles
- Information
- Copyright
- Copyright © The Association for Symbolic Logic 2015
References
REFERENCES
- 1
- Cited by


