Article contents
SMALL UNIVERSAL FAMILIES OF GRAPHS ON ℵω + 1
Published online by Cambridge University Press: 29 June 2016
Abstract
We prove that it is consistent that 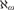 $\aleph _\omega $ is strong limit,
$\aleph _\omega $ is strong limit, 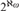 $2^{\aleph _\omega } $ is large and the universality number for graphs on
$2^{\aleph _\omega } $ is large and the universality number for graphs on 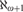 $\aleph _{\omega + 1} $ is small. The proof uses Prikry forcing with interleaved collapsing.
$\aleph _{\omega + 1} $ is small. The proof uses Prikry forcing with interleaved collapsing.
Keywords
- Type
- Articles
- Information
- Copyright
- Copyright © The Association for Symbolic Logic 2016
References
REFERENCES
- 1
- Cited by


