Skip to main content Accessibility help

We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.

Close cookie message
×
Home
  • Home
Hostname: page-component-559fc8cf4f-qpj69 Total loading time: 0.436 Render date: 2021-03-06T13:38:30.958Z Has data issue: true Feature Flags: { "shouldUseShareProductTool": true, "shouldUseHypothesis": true, "isUnsiloEnabled": true, "metricsAbstractViews": false, "figures": false, "newCiteModal": false, "newCitedByModal": true }
EnglishFrançais
The Journal of Symbolic Logic The Journal of Symbolic Logic

Article contents

Interpolation theorems, lower bounds for proof systems, and independence results for bounded arithmetic

Published online by Cambridge University Press:  12 March 2014

Jan Krajíček
Jan Krajíček
Affiliation:
Mathematical Institute of the Academy of Sciences, Žitná 25, Praha 1, 115 67, Czech Republic, E-mail: krajicek@mbox.cesnet.cz
Corresponding
E-mail address:
krajicek@mbox.cesnet.cz
Get access
Rights & Permissions[Opens in a new window]

Abstract

A proof of the (propositional) Craig interpolation theorem for cut-free sequent calculus yields that a sequent with a cut-free proof (or with a proof with cut-formulas of restricted form; in particular, with only analytic cuts) with k inferences has an interpolant whose circuit-size is at most k. We give a new proof of the interpolation theorem based on a communication complexity approach which allows a similar estimate for a larger class of proofs. We derive from it several corollaries:

  1. (1)Feasible interpolation theorems for the following proof systems:
    1. (a)resolution
    2. (b)a subsystem of LK corresponding to the bounded arithmetic theory 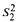(α)
    3. (c)linear equational calculus
    4. (d)cutting planes.
  2. (2)New proofs of the exponential lower bounds (for new formulas)
    1. (a)for resolution ([15])
    2. (b)for the cutting planes proof system with coefficients written in unary ([4]).
  3. (3)An alternative proof of the independence result of [43] concerning the provability of circuit-size lower bounds in the bounded arithmetic theory 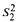(α).

In the other direction we show that a depth 2 subsystem of LK does not admit feasible monotone interpolation theorem (the so called Lyndon theorem), and that a feasible monotone interpolation theorem for the depth 1 subsystem of LK would yield new exponential lower bounds for resolution proofs of the weak pigeonhole principle.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 62 , Issue 2 , June 1997 , pp. 457 - 486
Copyright
Copyright © Association for Symbolic Logic 1997

Access options

Get access to the full version of this content by using one of the access options below.
If you should have access and can't see this content please contact technical support.

References

[1]Alon, N. and Boppana, R., The monotone circuit complexity of Boolean functions, Combinatorica, vol. 7 (1987), no. 1, pp. 1–22.CrossRefGoogle Scholar
[2]Andreev, A. E., On a method for obtaining lower bounds for the complexity of individual monotone functions, Doklady ANSSSR, vol. 282 (1985), no. 5, pp. 1033–1037, in Russian.Google Scholar
[3]Beth, E. W., The foundations of mathematics, North-Holland, Amsterdam, 1959.Google Scholar
[4]Bonet, M. L., Pitassi, T., and Raz, R., Lower bounds for cutting planes proofs with small coefficients, preprint, 1994.Google Scholar
[5]Buss, S. R., Bounded arithmetic, Bibliopolis, Naples, 1986.Google Scholar
[6]Buss, S. R. and Turán, G., Resolution proofs of generalized pigeonhole principles, Theoretical Computer Science, vol. 62 (1988), pp. 311–317.CrossRefGoogle Scholar
[7]Chiari, M. and Krajíček, J., Witnessing functions in bounded arithmetic and search problems, submitted, 1994.Google Scholar
[8]Cook, S. A., Feasibly constructive proofs and the prepositional calculus, Proceedings of the 7th Annual ACM Symposium on Theory of Computing, ACM Press, 1975, pp. 83–97.Google Scholar
[9]Cook, S. A. and Reckhow, A. R., The relative efficiency of prepositional proof systems, this Journal, vol. 44 (1979), no. 1, pp. 36–50.Google Scholar
[10]Cook, W., Coullard, C. R., and Turán, G., On the complexity of cutting plane proofs, Discrete Applied Mathematics, vol. 18 (1987), pp. 25–38.CrossRefGoogle Scholar
[11]Craig, W., Linear reasoning: A new form of the Herbrand-Gentzen theorem, this Journal, vol. 22 (1957), no. 3, pp. 250–268.Google Scholar
[12]Craig, W., Three uses of the Herbrand-Gentzen theorem in relating model theory and proof theory, this Journal, vol. 22 (1957), no. 3, pp. 269–285.Google Scholar
[13]Friedman, H., The complexity of explicit definitions, Advances in Mathematics, vol. 20 (1976), pp. 18–29.CrossRefGoogle Scholar
[14]Gurevich, Y., Towards logic tailored for computational complexity, Proceedings of Logic Colloquium 1983 (Berlin), Springer Lecture Notes in Mathematics, no. 1104, Springer-Verlag, 1984, pp. 175–216.Google Scholar
[15]Haken, A., The intractability of resolution, Theoretical Computer Science, vol. 39 (1985), pp. 297–308.CrossRefGoogle Scholar
[16]Karchmer, M. and Wigderson, A., Monotone circuits for connectivity require super-logarithmic depth, Proceedings of the 20th Annual ACM Symposium on Theory of Computing, ACM Press, 1988, pp. 539–550.Google Scholar
[17]Krajíček, J., Exponentiation and second-order bounded arithmetic, Annals of Pure and Applied Logic, vol. 48 (1989), pp. 261–276.CrossRefGoogle Scholar
[18]Krajíček, J., No counter-example interpretation and interactive computation, Logic from Computer Science, Proceedings of a workshop held November 13–17, 1989, in Berkeley, Mathematical Sciences Research Institute Publication (Berlin) (Moschovakis, Y. N., editor), no. 21, Springer-Verlag, 1992, pp. 287–293.Google Scholar
[19]Krajíček, J., Lower bounds to the size of constant-depth prepositional proofs, this Journal, vol. 59 (1994), no. 1, pp. 73–86.Google Scholar
[20]Krajíček, J., Bounded arithmetic, prepositional logic and complexity theory, Cambridge University Press, 1995.CrossRefGoogle Scholar
[21]Krajíček, J., On Frege and extended Frege proof systems, Feasible Mathematics II (Clote, P. and Remmel, J., editors), Birkhäuser, 1995, pp. 284–319.CrossRefGoogle Scholar
[22]Krajíček, J. and Pudlák, P., Prepositional proof systems, the consistency of first order theories and the complexity of computations, this Journal, vol. 54 (1989), no. 3, pp. 1063–1079.Google Scholar
[23]Krajíček, J., Prepositional provability in models of weak arithmetic, Computer Science Logic (Boerger, E., Kleine-Bunning, H., and Richter, M. M., editors), Lecture Notes in Computer Science, no. 440, Springer-Verlag, Berlin, 1990, Kaiserlautern, 10 1989, pp. 193–210.Google Scholar
[24]Krajíček, J., Quantified prepositional calculi and fragments of bounded arithmetic, Zeitschrift für Mathematikal Logik und Grundlagen der Mathematik, vol. 36 (1990), pp. 29–46.CrossRefGoogle Scholar
[25]Krajíček, J., Some consequences of cryptographical conjectures for and EF, Proceedings of the meeting Logic and Computational Complexity (Leivant, D., editor), 1995, Indianapolis, 10 1994, to appear.Google Scholar
[26]Krajíček, J. and Takeuti, G., On bounded -polynomial induction, Feasible mathematics (Buss, S. R. and Scott, P. J., editors), Birkhäuser, 1990, pp. 259–280.CrossRefGoogle Scholar
[27]Krajíček, J., On induction-free provability, Annals of Mathematics and Artificial Intelligence, vol. 6 (1992), pp. 107–126.CrossRefGoogle Scholar
[28]Kreisel, G., Technical report nb. 3, Applied Mathematics and Statistics Labs, Stanford University, unpublished, 1961.Google Scholar
[29]Luby, M., Pseudo-randomness and applications, International Computer Science Institute, Berkeley, lecture notes, 1993.Google Scholar
[30]Mundici, D., A lower bound for the complexity of Craig's interpolants in sentential logic, Archiv für Mathematikal Logik, vol. 23 (1983), pp. 27–36.CrossRefGoogle Scholar
[31]Mundici, D., NP and Craig's interpolation theorem, Proceedings of Logic Colloquium 1982, North-Holland, 1984, pp. 345–358.Google Scholar
[32]Mundici, D., Tautologies with a unique Craig interpolant, uniform vs. non-uniform complexity, Annals of Pure and Applied Logic, vol. 27 (1984), pp. 265–273.CrossRefGoogle Scholar
[33]Papadimitriou, A., Computational complexity, Addison-Wesley, 1994.Google Scholar
[34]Parikh, R., Existence and feasibility in arithmetic, this Journal, vol. 36 (1971), pp. 494–508.Google Scholar
[35]Paris, J. and Wilkie, A. J., Counting problems in bounded arithmetic, Methods in Mathematical Logic, Springer Lecture Notes in Mathematics, no. 1130, Springer-Verlag, Berlin, 1985, pp. 317–340.CrossRefGoogle Scholar
[36]Paris, J., On the scheme of induction for bounded arithmetic formulas, Annals of Pure and Applied Logic, vol. 35 (1987), pp. 261–302.Google Scholar
[37]Paris, J. B., Wilkie, A. J., and Woods, A. R., Provability of the pigeonhole principle and the existence of infinitely many primes, this Journal, vol. 53 (1988), pp. 1235–1244.Google Scholar
[38]Pratt, V. R., Every prime has a succinct certificate, SIAM Journal of Computing, vol. 4 (1975), pp. 214–220.CrossRefGoogle Scholar
[39]Razborov, A. A., Lower bounds on the monotone complexity of some Boolean functions, Soviet Mathem. Doklady, vol. 31 (1985), pp. 354–357.Google Scholar
[40]Razborov, A. A., An equivalence between second order bounded domain bounded arithmetic and first order bounded arithmetic, Arithmetic, Proof Theory and Computational Complexity (Clote, P. and Krajíček, J., editors), Oxford University Press, 1993, pp. 247–277.Google Scholar
[41]Razborov, A. A., On provably disjoint NP-pairs, preprint, 1994.Google Scholar
[42]Razborov, A. A., Bounded arithmetic and lower bounds in Boolean complexity, Feasible mathematics II (Clote, P. and Remmel, J., editors), Birkhäuser, 1995, pp. 344–386.CrossRefGoogle Scholar
[43]Razborov, A. A., Unprovability of lower bounds on the circuit size in certain fragments of bounded arithmetic, Izvestiya of the R. A. N., vol. 59 (1995), no. 1, pp. 201–224.Google Scholar
[44]Razborov, A.A. and Rudich, S., Natural proofs, Proceedings of the 26th Annual ACM Symposium on Theory of Computing, ACM Press, 1994, pp. 204–213.Google Scholar
[45]Takeuti, G., Proof theory, North-Holland, 1975.Google Scholar
[46]Takeuti, G., RSUV isomorphism, Arithmetic, Proof Theory and Computational Complexity (Clote, P. and Krajíček, J., editors), Oxford University Press, 1993, pp. 364–386.Google Scholar

Full text views

Full text views reflects PDF downloads, PDFs sent to Google Drive, Dropbox and Kindle and HTML full text views.

Total number of HTML views: 0
Total number of PDF views: 8 *
View data table for this chart

* Views captured on Cambridge Core between September 2016 - 6th March 2021. This data will be updated every 24 hours.

140 Cited by

Send article to Kindle

To send this article to your Kindle, first ensure no-reply@cambridge.org is added to your Approved Personal Document E-mail List under your Personal Document Settings on the Manage Your Content and Devices page of your Amazon account. Then enter the ‘name’ part of your Kindle email address below. Find out more about sending to your Kindle. Find out more about sending to your Kindle.

Note you can select to send to either the @free.kindle.com or @kindle.com variations. ‘@free.kindle.com’ emails are free but can only be sent to your device when it is connected to wi-fi. ‘@kindle.com’ emails can be delivered even when you are not connected to wi-fi, but note that service fees apply.

Find out more about the Kindle Personal Document Service.

Interpolation theorems, lower bounds for proof systems, and independence results for bounded arithmetic
Available formats
×

Send article to Dropbox

To send this article to your Dropbox account, please select one or more formats and confirm that you agree to abide by our usage policies. If this is the first time you use this feature, you will be asked to authorise Cambridge Core to connect with your <service> account. Find out more about sending content to Dropbox.

Interpolation theorems, lower bounds for proof systems, and independence results for bounded arithmetic
Available formats
×

Send article to Google Drive

To send this article to your Google Drive account, please select one or more formats and confirm that you agree to abide by our usage policies. If this is the first time you use this feature, you will be asked to authorise Cambridge Core to connect with your <service> account. Find out more about sending content to Google Drive.

Interpolation theorems, lower bounds for proof systems, and independence results for bounded arithmetic
Available formats
×
×

Reply to: Submit a response

Your details

Conflicting interests

Do you have any conflicting interests? *