No CrossRef data available.
Article contents
Effective presentability of Boolean algebras of Cantor-Bendixson rank 1
Published online by Cambridge University Press: 12 March 2014
Abstract
We show that there is a computable Boolean algebra 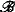 and a computably enumerable ideal I of
and a computably enumerable ideal I of 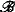 such that the quotient algebra
such that the quotient algebra 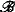 /I is of Cantor-Bendixson rank 1 and is not isomorphic to any computable Boolean algebra. This extends a result of L. Feiner and is deduced from Feiner's result even though Feiner's construction yields a Boolean algebra of infinite Cantor-Bendixson rank.
/I is of Cantor-Bendixson rank 1 and is not isomorphic to any computable Boolean algebra. This extends a result of L. Feiner and is deduced from Feiner's result even though Feiner's construction yields a Boolean algebra of infinite Cantor-Bendixson rank.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1999


