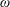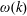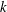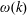1 Motivation
Since the advent of controlled laboratory experiments on electron–positron plasmas (Sarri et al.
Reference Sarri, Poder, Cole, Schumaker, di Piazza, Reville, Dzelzainis, Doria, Gizzi and Grittani2015), dispersion relations for waves in a pair plasma have become a diagnostic tool. Pair plasmas are created in pulsar magnetospheres or in the various flavours of ultrarelativistic astrophysical jets. Pair plasmas are also heavily studied using kinetic particle-in-cell codes, for e.g. reconnection aspects (Zenitani Reference Zenitani2018), shocks (Bret & Narayan Reference Bret and Narayan2018) and turbulence (Loureiro & Boldyrev Reference Loureiro and Boldyrev2018). The inherent symmetry in pair plasmas leaves three length scales of interest: the cyclotron radius
![]() $R_{e}$
(if magnetized), the plasma skin depth
$R_{e}$
(if magnetized), the plasma skin depth
![]() $\unicode[STIX]{x1D6FF}=c/\unicode[STIX]{x1D714}_{p}$
, where
$\unicode[STIX]{x1D6FF}=c/\unicode[STIX]{x1D714}_{p}$
, where
![]() $c$
is lightspeed and
$c$
is lightspeed and
![]() $\unicode[STIX]{x1D714}_{p}$
is the combined electron–positron plasma frequency, and the Debye length
$\unicode[STIX]{x1D714}_{p}$
is the combined electron–positron plasma frequency, and the Debye length
![]() $\unicode[STIX]{x1D706}_{D}$
. Laboratory pair plasmas may not necessarily achieve system sizes exceeding these wavelengths (Stenson et al.
Reference Stenson, Horn-Stanja, Stoneking and Sunn Pedersen2017), although most theory starts from spatially uniform conditions. Standard (Stix Reference Stix1992; Bittencourt Reference Bittencourt2004) and modern (Thorne & Blandford Reference Thorne and Blandford2017) textbooks describe the two-fluid viewpoint on a uniform, cold electron–ion plasma, to introduce the more complete kinetic viewpoint. Cold implies a vanishing
$\unicode[STIX]{x1D706}_{D}$
. Laboratory pair plasmas may not necessarily achieve system sizes exceeding these wavelengths (Stenson et al.
Reference Stenson, Horn-Stanja, Stoneking and Sunn Pedersen2017), although most theory starts from spatially uniform conditions. Standard (Stix Reference Stix1992; Bittencourt Reference Bittencourt2004) and modern (Thorne & Blandford Reference Thorne and Blandford2017) textbooks describe the two-fluid viewpoint on a uniform, cold electron–ion plasma, to introduce the more complete kinetic viewpoint. Cold implies a vanishing
![]() $\unicode[STIX]{x1D706}_{D}=0$
, and vanishing gyroradii when these are quantified through thermal speeds, to arrive at a zero plasma beta: we ignore all thermal pressure effects. The cold and two-fluid electron–ion assumptions imply that at fixed frequency
$\unicode[STIX]{x1D706}_{D}=0$
, and vanishing gyroradii when these are quantified through thermal speeds, to arrive at a zero plasma beta: we ignore all thermal pressure effects. The cold and two-fluid electron–ion assumptions imply that at fixed frequency
![]() $\unicode[STIX]{x1D714}$
, we have at most two waves that can propagate, and these are categorized as fast or slow, as right (R) or left (L) polarized, or of ordinary (O) or extraordinary (X) type. The latter two wave label pairs (R
$\unicode[STIX]{x1D714}$
, we have at most two waves that can propagate, and these are categorized as fast or slow, as right (R) or left (L) polarized, or of ordinary (O) or extraordinary (X) type. The latter two wave label pairs (R
![]() $/$
L and O
$/$
L and O
![]() $/$
X) relate to properties at
$/$
X) relate to properties at
![]() $\unicode[STIX]{x1D717}=0$
or
$\unicode[STIX]{x1D717}=0$
or
![]() $\unicode[STIX]{x1D717}=\unicode[STIX]{x03C0}/2$
, respectively, where
$\unicode[STIX]{x1D717}=\unicode[STIX]{x03C0}/2$
, respectively, where
![]() $\unicode[STIX]{x1D717}$
denotes the angle between the uniform magnetic field
$\unicode[STIX]{x1D717}$
denotes the angle between the uniform magnetic field
![]() $\boldsymbol{B}$
and the wavevector
$\boldsymbol{B}$
and the wavevector
![]() $\boldsymbol{k}$
(or unit vector
$\boldsymbol{k}$
(or unit vector
![]() $\hat{\boldsymbol{n}}=\boldsymbol{k}/k$
with wavenumber
$\hat{\boldsymbol{n}}=\boldsymbol{k}/k$
with wavenumber
![]() $k$
). For such cold plasmas, the Clemmow–Mullaly–Allis or CMA diagrams (Clemmow & Mullaly Reference Clemmow and Mullaly1955; Stix Reference Stix1992; Thorne & Blandford Reference Thorne and Blandford2017) display the large variety in wave normal surfaces, plotting dimensionless phase velocities
$k$
). For such cold plasmas, the Clemmow–Mullaly–Allis or CMA diagrams (Clemmow & Mullaly Reference Clemmow and Mullaly1955; Stix Reference Stix1992; Thorne & Blandford Reference Thorne and Blandford2017) display the large variety in wave normal surfaces, plotting dimensionless phase velocities
![]() $\unicode[STIX]{x1D714}/kc$
versus
$\unicode[STIX]{x1D714}/kc$
versus
![]() $\unicode[STIX]{x1D717}$
, when varying all relevant plasma parameters. In a cold two-fluid plasma, parameter space divides into 16 different regions, where either no, a single or a pair of topologically distinct wave normal surfaces can be expected. For a cold pair plasma, this CMA diagram simplifies considerably, leaving only 5 regions to consider, as the mass symmetry makes various limiting lines coincident. These limiting lines in the CMA viewpoint on cold, two-fluid plasmas correspond to special values, like 0 or
$\unicode[STIX]{x1D717}$
, when varying all relevant plasma parameters. In a cold two-fluid plasma, parameter space divides into 16 different regions, where either no, a single or a pair of topologically distinct wave normal surfaces can be expected. For a cold pair plasma, this CMA diagram simplifies considerably, leaving only 5 regions to consider, as the mass symmetry makes various limiting lines coincident. These limiting lines in the CMA viewpoint on cold, two-fluid plasmas correspond to special values, like 0 or
![]() $\infty$
, attained by the remaining dielectric tensor components. Another simplification in the cold pair plasma case is that the R and L labels become obsolete, as they both become
$\infty$
, attained by the remaining dielectric tensor components. Another simplification in the cold pair plasma case is that the R and L labels become obsolete, as they both become
where we introduced the dimensionless
![]() $\bar{\unicode[STIX]{x1D714}}=\unicode[STIX]{x1D714}/\unicode[STIX]{x1D714}_{p}$
and
$\bar{\unicode[STIX]{x1D714}}=\unicode[STIX]{x1D714}/\unicode[STIX]{x1D714}_{p}$
and
![]() $E=\unicode[STIX]{x1D6FA}_{e}/\unicode[STIX]{x1D714}_{p}$
, with
$E=\unicode[STIX]{x1D6FA}_{e}/\unicode[STIX]{x1D714}_{p}$
, with
![]() $\unicode[STIX]{x1D6FA}_{e}=eB/m_{e}$
the (positively defined) cyclotron frequency of interest. Despite these simplifications, the variety of wave modes in a cold pair plasma remains intricate, with O, X and Alfvén mode types as basic ingredients, together with their resonant (
$\unicode[STIX]{x1D6FA}_{e}=eB/m_{e}$
the (positively defined) cyclotron frequency of interest. Despite these simplifications, the variety of wave modes in a cold pair plasma remains intricate, with O, X and Alfvén mode types as basic ingredients, together with their resonant (
![]() $k\rightarrow \infty$
) or cutoff (
$k\rightarrow \infty$
) or cutoff (
![]() $k\rightarrow 0$
) behaviour. Waves in equal-mass plasmas were discussed in Stewart & Laing (Reference Stewart and Laing1992), Iwamoto (Reference Iwamoto1993) and Zank & Greaves (Reference Zank and Greaves1995), for cold and warm conditions, but our approach will reveal new aspects of cold pair plasma wave couplings and anisotropy. Pair plasmas have also been investigated in strongly magnetized (
$k\rightarrow 0$
) behaviour. Waves in equal-mass plasmas were discussed in Stewart & Laing (Reference Stewart and Laing1992), Iwamoto (Reference Iwamoto1993) and Zank & Greaves (Reference Zank and Greaves1995), for cold and warm conditions, but our approach will reveal new aspects of cold pair plasma wave couplings and anisotropy. Pair plasmas have also been investigated in strongly magnetized (
![]() $E\gg 1$
) conditions for pulsar magnetospheres (Lyutikov Reference Lyutikov1999), extending cold to warm regimes, including kinetic effects, using the usual approach based on dielectric tensor components. Extensions to account for different species bulk velocities and thermal effects are discussed in Lyutikov (Reference Lyutikov1998), where the kinetic treatment reveals the mode susceptibility to e.g. two-stream cyclotron or firehose instabilities. One may even include vacuum polarization effects, and obtain a dispersion relation with coupled X and O branches due to current densities along
$E\gg 1$
) conditions for pulsar magnetospheres (Lyutikov Reference Lyutikov1999), extending cold to warm regimes, including kinetic effects, using the usual approach based on dielectric tensor components. Extensions to account for different species bulk velocities and thermal effects are discussed in Lyutikov (Reference Lyutikov1998), where the kinetic treatment reveals the mode susceptibility to e.g. two-stream cyclotron or firehose instabilities. One may even include vacuum polarization effects, and obtain a dispersion relation with coupled X and O branches due to current densities along
![]() $\boldsymbol{B}$
and finite charge densities, as in Arons & Barnard (Reference Arons and Barnard1986). In our idealized two-fluid view, the X and O branches decouple, and all kinetic wave damping effects are ignored.
$\boldsymbol{B}$
and finite charge densities, as in Arons & Barnard (Reference Arons and Barnard1986). In our idealized two-fluid view, the X and O branches decouple, and all kinetic wave damping effects are ignored.
2 Cold pair plasma dispersion relation
Instead of using the dielectric tensor to obtain the dispersion relation, which has the advantage of retaining a three-by-three tensorial description when going to multiple ion–electron mixtures, the ideal two-fluid dispersion relation can also be derived from direct linearization of the equations of mass conservation, motion and energy conservation per species, combined with the full set of Maxwell equations (Goedbloed & Poedts Reference Goedbloed and Poedts2004). This leads to 14 degrees of freedom (both time-independent Maxwell equations reduce the original 16 by two), such that 14 wave modes are expected for any general (warm or cold) electron–ion mixture. Two of these modes are trivial and at marginal frequency, and this
![]() $\bar{\unicode[STIX]{x1D714}}^{2}=0$
pair relates to the single fluid magnetohydrodynamic (MHD) entropy wave. The remaining 12 can, by a judicious choice of variables, be obtained from the determinant of a symmetric
$\bar{\unicode[STIX]{x1D714}}^{2}=0$
pair relates to the single fluid magnetohydrodynamic (MHD) entropy wave. The remaining 12 can, by a judicious choice of variables, be obtained from the determinant of a symmetric
![]() $6\times 6$
matrix, where six pairs remain in a dispersion relation of sixth order in
$6\times 6$
matrix, where six pairs remain in a dispersion relation of sixth order in
![]() $\bar{\unicode[STIX]{x1D714}}^{2}$
(Goedbloed & Poedts Reference Goedbloed and Poedts2004). The symmetry of the matrix ensures that this is true at every real wavenumber
$\bar{\unicode[STIX]{x1D714}}^{2}$
(Goedbloed & Poedts Reference Goedbloed and Poedts2004). The symmetry of the matrix ensures that this is true at every real wavenumber
![]() $k$
. For the specific case of a cold pair plasma, this dispersion relation further factors out a trivial
$k$
. For the specific case of a cold pair plasma, this dispersion relation further factors out a trivial
![]() $\bar{\unicode[STIX]{x1D714}}^{2}=0$
pair: the slow magnetosonic MHD waves, which become marginal at zero temperature. This results in the 5 fundamental wave pairs discussed below.
$\bar{\unicode[STIX]{x1D714}}^{2}=0$
pair: the slow magnetosonic MHD waves, which become marginal at zero temperature. This results in the 5 fundamental wave pairs discussed below.
Defining
![]() $\bar{k}=\unicode[STIX]{x1D6FF}k$
, the dispersion relation becomes a quadratic in
$\bar{k}=\unicode[STIX]{x1D6FF}k$
, the dispersion relation becomes a quadratic in
![]() $\bar{k}^{2}$
with three cubic polynomials in
$\bar{k}^{2}$
with three cubic polynomials in
![]() $\bar{\unicode[STIX]{x1D714}}^{2}$
, but we will now systematically drop the overbars on
$\bar{\unicode[STIX]{x1D714}}^{2}$
, but we will now systematically drop the overbars on
![]() $\bar{\unicode[STIX]{x1D714}}$
and
$\bar{\unicode[STIX]{x1D714}}$
and
![]() $\bar{k}$
. The final 5 pairs then derive from
$\bar{k}$
. The final 5 pairs then derive from
where
![]() $\unicode[STIX]{x1D706}^{2}=\cos ^{2}\unicode[STIX]{x1D717}$
, and three third-order polynomials in
$\unicode[STIX]{x1D706}^{2}=\cos ^{2}\unicode[STIX]{x1D717}$
, and three third-order polynomials in
![]() $\unicode[STIX]{x1D714}^{2}$
given by
$\unicode[STIX]{x1D714}^{2}$
given by
We adopted a similar (but subtly different) notation as in standard, dielectric tensor-based treatments (Stix Reference Stix1992), which opt to rewrite (2.1) to a quadratic expression in the squared refractive index
![]() $n^{2}=k^{2}/\unicode[STIX]{x1D714}^{2}$
. Expressions (2.2) and (2.4) instantly reveal the three cutoff limits at
$n^{2}=k^{2}/\unicode[STIX]{x1D714}^{2}$
. Expressions (2.2) and (2.4) instantly reveal the three cutoff limits at
![]() $k\rightarrow 0$
, as
$k\rightarrow 0$
, as
![]() $C=0$
for
$C=0$
for
![]() $\unicode[STIX]{x1D714}^{2}=1$
(the plasma frequency) or
$\unicode[STIX]{x1D714}^{2}=1$
(the plasma frequency) or
![]() $\unicode[STIX]{x1D714}^{2}=1+E^{2}$
(twice). It also allows the resonance limits, computed from
$\unicode[STIX]{x1D714}^{2}=1+E^{2}$
(twice). It also allows the resonance limits, computed from
![]() $A=0$
, to be identified as
$A=0$
, to be identified as
![]() $\unicode[STIX]{x1D714}^{2}=E^{2}$
, and the pair of solutions
$\unicode[STIX]{x1D714}^{2}=E^{2}$
, and the pair of solutions
Note that
![]() $\unicode[STIX]{x1D714}_{-}^{2}$
decreases from its parallel value
$\unicode[STIX]{x1D714}_{-}^{2}$
decreases from its parallel value
![]() $\min [1,E^{2}]$
, to become
$\min [1,E^{2}]$
, to become
![]() $0$
at perpendicular orientation. At the same time,
$0$
at perpendicular orientation. At the same time,
![]() $\unicode[STIX]{x1D714}_{+}^{2}$
takes on values between
$\unicode[STIX]{x1D714}_{+}^{2}$
takes on values between
![]() $\max [1,E^{2}]$
for parallel propagation, and increases to
$\max [1,E^{2}]$
for parallel propagation, and increases to
![]() $1+E^{2}$
for perpendicular (
$1+E^{2}$
for perpendicular (
![]() $\unicode[STIX]{x1D706}=0$
).
$\unicode[STIX]{x1D706}=0$
).
Identification of the 5 branches at given wavenumber
![]() $k$
is aided as we factor (2.1) into
$k$
is aided as we factor (2.1) into
which is the X-branch, usually written as
![]() $n^{2}=R$
(this branch has wave electric field vector perpendicular to
$n^{2}=R$
(this branch has wave electric field vector perpendicular to
![]() $\boldsymbol{B}$
and
$\boldsymbol{B}$
and
![]() $\boldsymbol{k}$
, and represents transverse waves, see Stewart & Laing Reference Stewart and Laing1992), and the O-branch in
$\boldsymbol{k}$
, and represents transverse waves, see Stewart & Laing Reference Stewart and Laing1992), and the O-branch in
The polarization angles for the three O-branch solutions are more intricate, with varying angle between electric field and
![]() $\boldsymbol{k}$
, see e.g. figure 7 in Stewart & Laing (Reference Stewart and Laing1992). Thus far, our equations (2.6)–(2.7) are rewritten expressions, e.g. found in Lyutikov (Reference Lyutikov1999) (his equation (4.1), or in the extended preprint physics/9807022, his equations (11)–(12)), or in Stewart & Laing (Reference Stewart and Laing1992) (their equation (15)) where they appear in terms of
$\boldsymbol{k}$
, see e.g. figure 7 in Stewart & Laing (Reference Stewart and Laing1992). Thus far, our equations (2.6)–(2.7) are rewritten expressions, e.g. found in Lyutikov (Reference Lyutikov1999) (his equation (4.1), or in the extended preprint physics/9807022, his equations (11)–(12)), or in Stewart & Laing (Reference Stewart and Laing1992) (their equation (15)) where they appear in terms of
![]() $n^{2}$
. Their advantage is that they readily display the limits of purely parallel
$n^{2}$
. Their advantage is that they readily display the limits of purely parallel
![]() $\unicode[STIX]{x1D706}=1$
or perpendicular
$\unicode[STIX]{x1D706}=1$
or perpendicular
![]() $\unicode[STIX]{x1D706}=0$
propagation, where the five branches are easily factored. Actually, (2.6)–(2.7) can be factored for arbitrary
$\unicode[STIX]{x1D706}=0$
propagation, where the five branches are easily factored. Actually, (2.6)–(2.7) can be factored for arbitrary
![]() $\unicode[STIX]{x1D706}$
, using Cardano’s formulae for the latter branch, but we will only need their combined expressions.
$\unicode[STIX]{x1D706}$
, using Cardano’s formulae for the latter branch, but we will only need their combined expressions.
In conclusion of this section, note that the factorization of the full dispersion (2.1) into the sub-systems (2.6) and (2.7) is a fundamental one. As expanded in the following section, equation (2.6) describes the combined extraordinary electromagnetic (X) and fast magnetosonic (F) modes, whereas (2.7) describes the combined ordinary electromagnetic (O), modified electrostatic (M) and Alfvén (A) modes.
3 All waves in pair plasmas
3.1 Group speed expressions
Novel insight is obtained when we analyse the dispersion diagrams
![]() $\unicode[STIX]{x1D714}(k)$
for a given parameter
$\unicode[STIX]{x1D714}(k)$
for a given parameter
![]() $E$
, and use it to quantify the group speed expressions, valid for all wavenumbers and angles
$E$
, and use it to quantify the group speed expressions, valid for all wavenumbers and angles
![]() $\unicode[STIX]{x1D717}$
. From the X-branch in (2.6), we find two angle-independent solutions
$\unicode[STIX]{x1D717}$
. From the X-branch in (2.6), we find two angle-independent solutions
where the plus sign yields the electromagnetic X branch connecting the cutoff
![]() $1+E^{2}$
to light waves as
$1+E^{2}$
to light waves as
![]() $\lim _{k\rightarrow \infty }\unicode[STIX]{x1D714}^{2}=k^{2}$
. The other angle-independent X-branch, which we label as
$\lim _{k\rightarrow \infty }\unicode[STIX]{x1D714}^{2}=k^{2}$
. The other angle-independent X-branch, which we label as
![]() $\unicode[STIX]{x1D714}_{\text{F}}$
, has a minus sign before the square root in (3.1), and is directly linked to the fast MHD modes, since
$\unicode[STIX]{x1D714}_{\text{F}}$
, has a minus sign before the square root in (3.1), and is directly linked to the fast MHD modes, since
![]() $\lim _{k\rightarrow 0}\unicode[STIX]{x1D714}^{2}/k^{2}=E^{2}/(1+E^{2})$
. At (cyclotron) resonance, this branch has
$\lim _{k\rightarrow 0}\unicode[STIX]{x1D714}^{2}/k^{2}=E^{2}/(1+E^{2})$
. At (cyclotron) resonance, this branch has
![]() $\lim _{k\rightarrow \infty }\unicode[STIX]{x1D714}^{2}=E^{2}$
. For both branches, it is easy to quantify the phase speed and group speed for every value of
$\lim _{k\rightarrow \infty }\unicode[STIX]{x1D714}^{2}=E^{2}$
. For both branches, it is easy to quantify the phase speed and group speed for every value of
![]() $k$
, and the latter are
$k$
, and the latter are
with the plus sign for the electromagnetic X branch
![]() $\unicode[STIX]{x1D714}_{\text{X}}(k)$
, and the minus sign for the fast branch
$\unicode[STIX]{x1D714}_{\text{X}}(k)$
, and the minus sign for the fast branch
![]() $\unicode[STIX]{x1D714}_{\text{F}}(k)$
. This is an isotropic circle (sphere) at all wavenumbers, and the
$\unicode[STIX]{x1D714}_{\text{F}}(k)$
. This is an isotropic circle (sphere) at all wavenumbers, and the
![]() $\unicode[STIX]{x1D714}_{\text{F}}$
one has vanishing radius
$\unicode[STIX]{x1D714}_{\text{F}}$
one has vanishing radius
![]() $\propto 1/k^{3}$
as
$\propto 1/k^{3}$
as
![]() $k\rightarrow \infty$
, while at small wavenumbers, it retrieves the fast part
$k\rightarrow \infty$
, while at small wavenumbers, it retrieves the fast part
![]() $\pm E\hat{\boldsymbol{n}}/\sqrt{1+E^{2}}$
of the well-known MHD Friedrichs diagram showing the group speed for all angles
$\pm E\hat{\boldsymbol{n}}/\sqrt{1+E^{2}}$
of the well-known MHD Friedrichs diagram showing the group speed for all angles
![]() $\unicode[STIX]{x1D717}$
. The
$\unicode[STIX]{x1D717}$
. The
![]() $\unicode[STIX]{x1D714}_{\text{X}}$
mode also has a circular group diagram, with radius
$\unicode[STIX]{x1D714}_{\text{X}}$
mode also has a circular group diagram, with radius
![]() $k/(1+E^{2})^{3/2}$
at large wavelengths, while tending to the light circle
$k/(1+E^{2})^{3/2}$
at large wavelengths, while tending to the light circle
![]() $\unicode[STIX]{x2202}\unicode[STIX]{x1D714}/\unicode[STIX]{x2202}\boldsymbol{k}\rightarrow \pm \hat{\boldsymbol{n}}$
at large
$\unicode[STIX]{x2202}\unicode[STIX]{x1D714}/\unicode[STIX]{x2202}\boldsymbol{k}\rightarrow \pm \hat{\boldsymbol{n}}$
at large
![]() $k$
, appropriate for light waves.
$k$
, appropriate for light waves.
We can use (2.7) to deduce the governing group speed expression on all three other branches, which we will label as
![]() $\unicode[STIX]{x1D714}_{\text{O,M,A}}$
, written in a manner that aids direct evaluation for limits towards small and large wavenumbers. We use implicit derivation to
$\unicode[STIX]{x1D714}_{\text{O,M,A}}$
, written in a manner that aids direct evaluation for limits towards small and large wavenumbers. We use implicit derivation to
![]() $\unicode[STIX]{x2202}/\unicode[STIX]{x2202}\boldsymbol{k}$
, noting that
$\unicode[STIX]{x2202}/\unicode[STIX]{x2202}\boldsymbol{k}$
, noting that
![]() $\unicode[STIX]{x2202}k^{2}/\unicode[STIX]{x2202}\boldsymbol{k}=2\boldsymbol{k}$
and
$\unicode[STIX]{x2202}k^{2}/\unicode[STIX]{x2202}\boldsymbol{k}=2\boldsymbol{k}$
and
![]() $\unicode[STIX]{x2202}\unicode[STIX]{x1D706}^{2}/\unicode[STIX]{x2202}\boldsymbol{k}=2\unicode[STIX]{x1D706}/k[\hat{\boldsymbol{b}}-\unicode[STIX]{x1D706}\hat{\boldsymbol{n}}]$
where
$\unicode[STIX]{x2202}\unicode[STIX]{x1D706}^{2}/\unicode[STIX]{x2202}\boldsymbol{k}=2\unicode[STIX]{x1D706}/k[\hat{\boldsymbol{b}}-\unicode[STIX]{x1D706}\hat{\boldsymbol{n}}]$
where
![]() $\hat{\boldsymbol{b}}=\boldsymbol{B}/B$
, and write their group speed as
$\hat{\boldsymbol{b}}=\boldsymbol{B}/B$
, and write their group speed as
This general expression can be used to derive all small and large wavenumber limits. To do so, we note that (2.7) can be rewritten in terms of refractive index as
![]() $n^{2}=(\unicode[STIX]{x1D714}^{2}-1)(\unicode[STIX]{x1D714}^{2}-1-E^{2})/[\unicode[STIX]{x1D706}^{2}E^{2}+\unicode[STIX]{x1D714}^{2}(\unicode[STIX]{x1D714}^{2}-1-E^{2})]$
. From this expression, low frequency limits render us the Alfvén branch where
$n^{2}=(\unicode[STIX]{x1D714}^{2}-1)(\unicode[STIX]{x1D714}^{2}-1-E^{2})/[\unicode[STIX]{x1D706}^{2}E^{2}+\unicode[STIX]{x1D714}^{2}(\unicode[STIX]{x1D714}^{2}-1-E^{2})]$
. From this expression, low frequency limits render us the Alfvén branch where
![]() $\unicode[STIX]{x1D714}^{2}=\unicode[STIX]{x1D706}^{2}k^{2}E^{2}/(1+E^{2})$
, while high frequency behaviour becomes electromagnetic, or
$\unicode[STIX]{x1D714}^{2}=\unicode[STIX]{x1D706}^{2}k^{2}E^{2}/(1+E^{2})$
, while high frequency behaviour becomes electromagnetic, or
![]() $\unicode[STIX]{x1D714}^{2}\propto k^{2}$
. More precisely, the same expression can be shown to give
$\unicode[STIX]{x1D714}^{2}\propto k^{2}$
. More precisely, the same expression can be shown to give
![]() $\lim _{k\rightarrow \infty }\unicode[STIX]{x1D714}^{2}=1+k^{2}$
, for the electromagnetic O-branch.
$\lim _{k\rightarrow \infty }\unicode[STIX]{x1D714}^{2}=1+k^{2}$
, for the electromagnetic O-branch.
We now analyse (3.3) in all relevant limits, and find for the behaviour as
![]() $k\rightarrow 0$
while Alfvénic, the familiar
$k\rightarrow 0$
while Alfvénic, the familiar
which is the purely point-like group speed of Alfvén waves, also part of the MHD Friedrichs diagram. Anticipating that this
![]() $\unicode[STIX]{x1D714}_{\text{A}}(k,\unicode[STIX]{x1D717})$
branch will transform to resonant behaviour and will normally connect to
$\unicode[STIX]{x1D714}_{\text{A}}(k,\unicode[STIX]{x1D717})$
branch will transform to resonant behaviour and will normally connect to
![]() $\unicode[STIX]{x1D714}_{-}$
(see next section), we find at resonance
$\unicode[STIX]{x1D714}_{-}$
(see next section), we find at resonance
At the branch to the
![]() $\unicode[STIX]{x1D714}_{+}$
resonance, which will be labelled as
$\unicode[STIX]{x1D714}_{+}$
resonance, which will be labelled as
![]() $\unicode[STIX]{x1D714}_{\text{M}}(k,\unicode[STIX]{x1D717})$
as this will modify the electrostatic cutoff
$\unicode[STIX]{x1D714}_{\text{M}}(k,\unicode[STIX]{x1D717})$
as this will modify the electrostatic cutoff
![]() $\unicode[STIX]{x1D714}_{\text{M}}(k\rightarrow 0)=1$
, we find a similar expression, namely
$\unicode[STIX]{x1D714}_{\text{M}}(k\rightarrow 0)=1$
, we find a similar expression, namely
The behaviour for the electromagnetic O-branch going as
![]() $\unicode[STIX]{x1D714}^{2}=1+k^{2}$
is to leading order the expected
$\unicode[STIX]{x1D714}^{2}=1+k^{2}$
is to leading order the expected
![]() $\unicode[STIX]{x2202}\unicode[STIX]{x1D714}/\unicode[STIX]{x2202}\boldsymbol{k}\rightarrow \pm \hat{\boldsymbol{n}}$
at large
$\unicode[STIX]{x2202}\unicode[STIX]{x1D714}/\unicode[STIX]{x2202}\boldsymbol{k}\rightarrow \pm \hat{\boldsymbol{n}}$
at large
![]() $k$
. At the remaining two cutoffs, we find extreme anisotropic behaviour. For
$k$
. At the remaining two cutoffs, we find extreme anisotropic behaviour. For
![]() $\unicode[STIX]{x1D714}_{\text{M}}(k\rightarrow 0)$
at the plasma frequency cutoff, we find
$\unicode[STIX]{x1D714}_{\text{M}}(k\rightarrow 0)$
at the plasma frequency cutoff, we find
where we used the freedom to take
![]() $\hat{\boldsymbol{b}}=(1,0)$
and
$\hat{\boldsymbol{b}}=(1,0)$
and
![]() $\hat{\boldsymbol{n}}=(\cos \unicode[STIX]{x1D717},\sin \unicode[STIX]{x1D717})$
. Equation (3.7) represents energy transport purely perpendicular to the magnetic field, in the
$\hat{\boldsymbol{n}}=(\cos \unicode[STIX]{x1D717},\sin \unicode[STIX]{x1D717})$
. Equation (3.7) represents energy transport purely perpendicular to the magnetic field, in the
![]() $\boldsymbol{k}-\boldsymbol{B}$
plane. Finally, for the other cutoff at
$\boldsymbol{k}-\boldsymbol{B}$
plane. Finally, for the other cutoff at
![]() $1+E^{2}$
which defines the start of the remaining
$1+E^{2}$
which defines the start of the remaining
![]() $\unicode[STIX]{x1D714}_{\text{O}}(k,\unicode[STIX]{x1D717})$
branch, we get
$\unicode[STIX]{x1D714}_{\text{O}}(k,\unicode[STIX]{x1D717})$
branch, we get
Equation (3.8) represents energy transport purely along the magnetic field. We will show later the visual confirmation of all these limits, at both small and large wavelengths, but the actual variation implied by (3.3) is extremely intricate, especially near
![]() $k\approx O(1)$
. We first turn attention to a judicious labelling of branches.
$k\approx O(1)$
. We first turn attention to a judicious labelling of branches.
3.2 Avoided crossings of branches
In this section, we discuss the complete dispersion
![]() $\unicode[STIX]{x1D714}(k)$
diagrams for varying
$\unicode[STIX]{x1D714}(k)$
diagrams for varying
![]() $\unicode[STIX]{x1D717}\in [0,\unicode[STIX]{x03C0}/2]$
. At
$\unicode[STIX]{x1D717}\in [0,\unicode[STIX]{x03C0}/2]$
. At
![]() $\unicode[STIX]{x1D706}=1$
or parallel propagation
$\unicode[STIX]{x1D706}=1$
or parallel propagation
![]() $\unicode[STIX]{x1D717}=0$
, the 3 branches mixed up in (2.7) are an
$\unicode[STIX]{x1D717}=0$
, the 3 branches mixed up in (2.7) are an
![]() $\unicode[STIX]{x1D714}_{\text{A}}$
Alfvénic branch that overlaps with the fast
$\unicode[STIX]{x1D714}_{\text{A}}$
Alfvénic branch that overlaps with the fast
![]() $\unicode[STIX]{x1D714}_{\text{F}}$
one (hence
$\unicode[STIX]{x1D714}_{\text{F}}$
one (hence
![]() $\unicode[STIX]{x1D714}_{\text{A}}(k,\unicode[STIX]{x1D717}=0)$
has the same cyclotron resonant behaviour), an electromagnetic
$\unicode[STIX]{x1D714}_{\text{A}}(k,\unicode[STIX]{x1D717}=0)$
has the same cyclotron resonant behaviour), an electromagnetic
![]() $\unicode[STIX]{x1D714}_{\text{O}}$
one that is identical to
$\unicode[STIX]{x1D714}_{\text{O}}$
one that is identical to
![]() $\unicode[STIX]{x1D714}_{\text{X}}$
from (3.1) and the electrostatic
$\unicode[STIX]{x1D714}_{\text{X}}$
from (3.1) and the electrostatic
![]() $\unicode[STIX]{x1D714}^{2}=1$
mode pair. It does seem that only 3 modes are left, but two are doubly degenerate. Also for this parallel case, when
$\unicode[STIX]{x1D714}^{2}=1$
mode pair. It does seem that only 3 modes are left, but two are doubly degenerate. Also for this parallel case, when
![]() $E>1$
, the coincident
$E>1$
, the coincident
![]() $\unicode[STIX]{x1D714}_{\text{A}}$
and
$\unicode[STIX]{x1D714}_{\text{A}}$
and
![]() $\unicode[STIX]{x1D714}_{\text{F}}$
branches obviously intersect the electrostatic branch, and this happens at
$\unicode[STIX]{x1D714}_{\text{F}}$
branches obviously intersect the electrostatic branch, and this happens at
![]() $\unicode[STIX]{x1D714}^{2}=1$
,
$\unicode[STIX]{x1D714}^{2}=1$
,
![]() $k^{2}=E^{2}/(E^{2}-1)$
. This intersection was already noted, albeit in approximate form for
$k^{2}=E^{2}/(E^{2}-1)$
. This intersection was already noted, albeit in approximate form for
![]() $E\gg 1$
only, in Lyutikov (Reference Lyutikov1999) (preprint version, equation (15)). At exactly perpendicular propagation, a similarly complete factorization of all 5 wave modes is easily achieved, since now for
$E\gg 1$
only, in Lyutikov (Reference Lyutikov1999) (preprint version, equation (15)). At exactly perpendicular propagation, a similarly complete factorization of all 5 wave modes is easily achieved, since now for
![]() $\unicode[STIX]{x1D706}=0$
the Alfvénic branch becomes marginal
$\unicode[STIX]{x1D706}=0$
the Alfvénic branch becomes marginal
![]() $\unicode[STIX]{x1D714}_{A}^{2}=0$
and the two branches remaining in (2.7) become
$\unicode[STIX]{x1D714}_{A}^{2}=0$
and the two branches remaining in (2.7) become
![]() $\unicode[STIX]{x1D714}^{2}=1+k^{2}$
and
$\unicode[STIX]{x1D714}^{2}=1+k^{2}$
and
![]() $\unicode[STIX]{x1D714}^{2}=1+E^{2}$
. Clearly, the latter two branches also intersect, and this for the values
$\unicode[STIX]{x1D714}^{2}=1+E^{2}$
. Clearly, the latter two branches also intersect, and this for the values
![]() $\unicode[STIX]{x1D714}^{2}=1+E^{2}$
,
$\unicode[STIX]{x1D714}^{2}=1+E^{2}$
,
![]() $k^{2}=E^{2}$
. Hence, the extreme cases of pure parallel or pure perpendicular propagation are exactly known, and those are typically used to start the subsequent categorization of plasma wave modes. However, both cases are rather exceptional, as we demonstrate now.
$k^{2}=E^{2}$
. Hence, the extreme cases of pure parallel or pure perpendicular propagation are exactly known, and those are typically used to start the subsequent categorization of plasma wave modes. However, both cases are rather exceptional, as we demonstrate now.
Indeed, drawing and analysing the dispersion diagrams for all angles
![]() $0<\unicode[STIX]{x1D717}<\unicode[STIX]{x03C0}/2$
, it is noted that the ordering of all 5 branches is unaltered for all wavenumbers
$0<\unicode[STIX]{x1D717}<\unicode[STIX]{x03C0}/2$
, it is noted that the ordering of all 5 branches is unaltered for all wavenumbers
![]() $k$
, and is such that
$k$
, and is such that
![]() $\unicode[STIX]{x1D714}_{\text{A}}<\unicode[STIX]{x1D714}_{\text{F}}<\unicode[STIX]{x1D714}_{\text{M}}<\unicode[STIX]{x1D714}_{\text{O}}<\unicode[STIX]{x1D714}_{\text{X}}$
, where we labelled the branches as Alfvénic, fast, modified electrostatic and both O and X electromagnetic types. At all angles except
$\unicode[STIX]{x1D714}_{\text{A}}<\unicode[STIX]{x1D714}_{\text{F}}<\unicode[STIX]{x1D714}_{\text{M}}<\unicode[STIX]{x1D714}_{\text{O}}<\unicode[STIX]{x1D714}_{\text{X}}$
, where we labelled the branches as Alfvénic, fast, modified electrostatic and both O and X electromagnetic types. At all angles except
![]() $0$
or
$0$
or
![]() $\unicode[STIX]{x03C0}/2$
, branches do not cross, and can be best ordered according to the way in which their robust small wavenumber behaviour (and their associated group speed appearance) connects to the large wavenumber behaviour. In figure 1, we show dispersion diagrams for 4 representative angles for a case with
$\unicode[STIX]{x03C0}/2$
, branches do not cross, and can be best ordered according to the way in which their robust small wavenumber behaviour (and their associated group speed appearance) connects to the large wavenumber behaviour. In figure 1, we show dispersion diagrams for 4 representative angles for a case with
![]() $E=1.5$
. This
$E=1.5$
. This
![]() $E$
-value is chosen to show both avoided crossings mentioned (only one appears when
$E$
-value is chosen to show both avoided crossings mentioned (only one appears when
![]() $E\leqslant 1$
), and represents a case where one can not rely on approximations using
$E\leqslant 1$
), and represents a case where one can not rely on approximations using
![]() $E\gg 1$
. The second diagram of figure 1 (taken at
$E\gg 1$
. The second diagram of figure 1 (taken at
![]() $\unicode[STIX]{x1D717}=\unicode[STIX]{x03C0}/3$
) shows clearly how (i) the angle-dependent
$\unicode[STIX]{x1D717}=\unicode[STIX]{x03C0}/3$
) shows clearly how (i) the angle-dependent
![]() $\unicode[STIX]{x1D714}_{\text{A}}(k,\unicode[STIX]{x1D717})$
branch connects the Alfvén group diagram at small
$\unicode[STIX]{x1D714}_{\text{A}}(k,\unicode[STIX]{x1D717})$
branch connects the Alfvén group diagram at small
![]() $k$
to the
$k$
to the
![]() $\unicode[STIX]{x1D714}_{-}$
resonance, and (ii) the angle-independent
$\unicode[STIX]{x1D714}_{-}$
resonance, and (ii) the angle-independent
![]() $\unicode[STIX]{x1D714}_{\text{F}}(k)$
branch lies above
$\unicode[STIX]{x1D714}_{\text{F}}(k)$
branch lies above
![]() $\unicode[STIX]{x1D714}_{\text{A}}$
in frequency, and connects the fast circular group speed at small
$\unicode[STIX]{x1D714}_{\text{A}}$
in frequency, and connects the fast circular group speed at small
![]() $k$
to the cyclotron
$k$
to the cyclotron
![]() $\unicode[STIX]{x1D714}=E$
resonance. Above
$\unicode[STIX]{x1D714}=E$
resonance. Above
![]() $\unicode[STIX]{x1D714}_{\text{F}}$
lies the modified electrostatic branch which we indicated with
$\unicode[STIX]{x1D714}_{\text{F}}$
lies the modified electrostatic branch which we indicated with
![]() $\unicode[STIX]{x1D714}_{\text{M}}(k,\unicode[STIX]{x1D717})$
, which connects the lowest cutoff
$\unicode[STIX]{x1D714}_{\text{M}}(k,\unicode[STIX]{x1D717})$
, which connects the lowest cutoff
![]() $\unicode[STIX]{x1D714}=1$
with the highest resonance
$\unicode[STIX]{x1D714}=1$
with the highest resonance
![]() $\unicode[STIX]{x1D714}_{+}$
. The remaining
$\unicode[STIX]{x1D714}_{+}$
. The remaining
![]() $\unicode[STIX]{x1D714}_{\text{O,X}}$
branches both start at the (coincident) cutoff where
$\unicode[STIX]{x1D714}_{\text{O,X}}$
branches both start at the (coincident) cutoff where
![]() $\unicode[STIX]{x1D714}=\sqrt{1+E^{2}}$
, and go off to their light speed behaviour at small wavelength (large
$\unicode[STIX]{x1D714}=\sqrt{1+E^{2}}$
, and go off to their light speed behaviour at small wavelength (large
![]() $k$
). The fact that this happens for all
$k$
). The fact that this happens for all
![]() $0<\unicode[STIX]{x1D717}<\unicode[STIX]{x03C0}/2$
should be appreciated as avoided crossings of branches, which is illustrated in figure 1 by drawing the dispersion relation also for two extremely small deviations from parallel (i.e.
$0<\unicode[STIX]{x1D717}<\unicode[STIX]{x03C0}/2$
should be appreciated as avoided crossings of branches, which is illustrated in figure 1 by drawing the dispersion relation also for two extremely small deviations from parallel (i.e.
![]() $\unicode[STIX]{x1D717}=\unicode[STIX]{x1D716}$
) or perpendicular (i.e.
$\unicode[STIX]{x1D717}=\unicode[STIX]{x1D716}$
) or perpendicular (i.e.
![]() $\unicode[STIX]{x1D717}=\unicode[STIX]{x03C0}/2-\unicode[STIX]{x1D716}$
) orientation, where we took
$\unicode[STIX]{x1D717}=\unicode[STIX]{x03C0}/2-\unicode[STIX]{x1D716}$
) orientation, where we took
![]() $\unicode[STIX]{x1D716}=0.002$
for illustration purposes. The avoided crossings are only clear when zooming in on the regions of interest, i.e. at the values
$\unicode[STIX]{x1D716}=0.002$
for illustration purposes. The avoided crossings are only clear when zooming in on the regions of interest, i.e. at the values
![]() $(\sqrt{1+E^{2}},E)$
(for near perpendicular) and
$(\sqrt{1+E^{2}},E)$
(for near perpendicular) and
![]() $(1,\sqrt{E^{2}/(E^{2}-1)})$
(near parallel), and these are shown as figure insets. The latter, near-parallel behaviour is also discussed in Lyutikov (Reference Lyutikov1999), but this particular avoided crossing is obviously only relevant for cases where
$(1,\sqrt{E^{2}/(E^{2}-1)})$
(near parallel), and these are shown as figure insets. The latter, near-parallel behaviour is also discussed in Lyutikov (Reference Lyutikov1999), but this particular avoided crossing is obviously only relevant for cases where
![]() $E>1$
. In that sense, the avoided crossing between the
$E>1$
. In that sense, the avoided crossing between the
![]() $\unicode[STIX]{x1D714}_{\text{M}}$
(purple branch in figure 1) and the
$\unicode[STIX]{x1D714}_{\text{M}}$
(purple branch in figure 1) and the
![]() $\unicode[STIX]{x1D714}_{\text{O}}$
branch (cyan in the figure) at near-perpendicular propagation, is more robust, as it occurs at all values of
$\unicode[STIX]{x1D714}_{\text{O}}$
branch (cyan in the figure) at near-perpendicular propagation, is more robust, as it occurs at all values of
![]() $E>0$
.
$E>0$
.

Figure 1. The dispersion diagram showing all 5
![]() $\unicode[STIX]{x1D714}(k)$
branches for a pair plasma with
$\unicode[STIX]{x1D714}(k)$
branches for a pair plasma with
![]() $E=1.5$
. Panels (a–d) differ in angle
$E=1.5$
. Panels (a–d) differ in angle
![]() $\unicode[STIX]{x1D717}$
between wavevector and magnetic field. An animation of the variation with
$\unicode[STIX]{x1D717}$
between wavevector and magnetic field. An animation of the variation with
![]() $\unicode[STIX]{x1D717}$
is given in the supplementary material, in the movie DispersionRelation.mp4 available at https://doi.org/10.1017/S0022377819000102. The thin dashed line indicates light speed behaviour. Insets for near-parallel or perpendicular angles
$\unicode[STIX]{x1D717}$
is given in the supplementary material, in the movie DispersionRelation.mp4 available at https://doi.org/10.1017/S0022377819000102. The thin dashed line indicates light speed behaviour. Insets for near-parallel or perpendicular angles
![]() $\unicode[STIX]{x1D717}$
illustrate avoided crossings. Branches are coloured black (angle-independent
$\unicode[STIX]{x1D717}$
illustrate avoided crossings. Branches are coloured black (angle-independent
![]() $\unicode[STIX]{x1D714}_{\text{X}}(k)$
), blue (angle-independent
$\unicode[STIX]{x1D714}_{\text{X}}(k)$
), blue (angle-independent
![]() $\unicode[STIX]{x1D714}_{\text{F}}(k)$
), cyan (
$\unicode[STIX]{x1D714}_{\text{F}}(k)$
), cyan (
![]() $\unicode[STIX]{x1D714}_{\text{O}}(k,\unicode[STIX]{x1D717})$
), purple (
$\unicode[STIX]{x1D714}_{\text{O}}(k,\unicode[STIX]{x1D717})$
), purple (
![]() $\unicode[STIX]{x1D714}_{\text{M}}(k,\unicode[STIX]{x1D717})$
) and red (
$\unicode[STIX]{x1D714}_{\text{M}}(k,\unicode[STIX]{x1D717})$
) and red (
![]() $\unicode[STIX]{x1D714}_{\text{A}}(k,\unicode[STIX]{x1D717})$
). The
$\unicode[STIX]{x1D714}_{\text{A}}(k,\unicode[STIX]{x1D717})$
). The
![]() $\unicode[STIX]{x1D714}_{\text{X}}$
branch uses dashes, to better distinguish it from the
$\unicode[STIX]{x1D714}_{\text{X}}$
branch uses dashes, to better distinguish it from the
![]() $\unicode[STIX]{x1D714}_{\text{O}}$
branch which nearly overlaps.
$\unicode[STIX]{x1D714}_{\text{O}}$
branch which nearly overlaps.
The near-parallel avoided crossing becomes a true crossing of branches at exactly parallel propagation, as then the
![]() $\unicode[STIX]{x1D714}_{\text{A}}(k,0)$
branch suddenly connects to the
$\unicode[STIX]{x1D714}_{\text{A}}(k,0)$
branch suddenly connects to the
![]() $\unicode[STIX]{x1D714}_{+}$
resonance, which coincides with the cyclotron resonance
$\unicode[STIX]{x1D714}_{+}$
resonance, which coincides with the cyclotron resonance
![]() $E$
at this angle. The near-perpendicular avoided crossing becomes a true crossing at exactly perpendicular propagation, when this time the
$E$
at this angle. The near-perpendicular avoided crossing becomes a true crossing at exactly perpendicular propagation, when this time the
![]() $\unicode[STIX]{x1D714}_{\text{M}}(k,\unicode[STIX]{x03C0}/2)$
(purple) branch connects to light waves, while the (cyan)
$\unicode[STIX]{x1D714}_{\text{M}}(k,\unicode[STIX]{x03C0}/2)$
(purple) branch connects to light waves, while the (cyan)
![]() $\unicode[STIX]{x1D714}_{\text{O}}$
branch becomes of constant frequency
$\unicode[STIX]{x1D714}_{\text{O}}$
branch becomes of constant frequency
![]() $\sqrt{1+E^{2}}$
, which is the
$\sqrt{1+E^{2}}$
, which is the
![]() $\unicode[STIX]{x1D714}_{+}$
resonance for this angle. These avoided crossings are related to the observation that the original dispersion relation is only quadratic in
$\unicode[STIX]{x1D714}_{+}$
resonance for this angle. These avoided crossings are related to the observation that the original dispersion relation is only quadratic in
![]() $k^{2}$
, such that at fixed real frequency (i.e. at every horizontal intersection through our dispersion diagrams), at most two wave modes can be found. This observation is at the basis of the CMA diagrams, and is embedded in all theory regarding cold two-fluid plasma waves, which labels wave types as fast or slow, L
$k^{2}$
, such that at fixed real frequency (i.e. at every horizontal intersection through our dispersion diagrams), at most two wave modes can be found. This observation is at the basis of the CMA diagrams, and is embedded in all theory regarding cold two-fluid plasma waves, which labels wave types as fast or slow, L
![]() $/$
R or X
$/$
R or X
![]() $/$
O at fixed frequency. However, this accepted naming convention is confusing, since our fast
$/$
O at fixed frequency. However, this accepted naming convention is confusing, since our fast
![]() $\unicode[STIX]{x1D714}_{\text{F}}$
branch then changes label from fast when
$\unicode[STIX]{x1D714}_{\text{F}}$
branch then changes label from fast when
![]() $\unicode[STIX]{x1D714}_{\text{F}}<1$
, to slow for
$\unicode[STIX]{x1D714}_{\text{F}}<1$
, to slow for
![]() $1<\unicode[STIX]{x1D714}_{\text{F}}<E$
, for the case displayed in figure 1. Moreover, the cold assumption got rid of the MHD slow mode, which enriches the classification when a warm plasma is considered. Finally, even the extraordinary (X) versus ordinary (O) mode label seems misleading, as the X-branch is not showing any special behaviour: both its modes (
$1<\unicode[STIX]{x1D714}_{\text{F}}<E$
, for the case displayed in figure 1. Moreover, the cold assumption got rid of the MHD slow mode, which enriches the classification when a warm plasma is considered. Finally, even the extraordinary (X) versus ordinary (O) mode label seems misleading, as the X-branch is not showing any special behaviour: both its modes (
![]() $\unicode[STIX]{x1D714}_{\text{F}}$
and
$\unicode[STIX]{x1D714}_{\text{F}}$
and
![]() $\unicode[STIX]{x1D714}_{\text{X}}$
) are angle independent and do not show any coupling to other branches, in contrast to all 3 mode pairs
$\unicode[STIX]{x1D714}_{\text{X}}$
) are angle independent and do not show any coupling to other branches, in contrast to all 3 mode pairs
![]() $\unicode[STIX]{x1D714}_{\text{A,M,O}}$
from the O-branch family.
$\unicode[STIX]{x1D714}_{\text{A,M,O}}$
from the O-branch family.
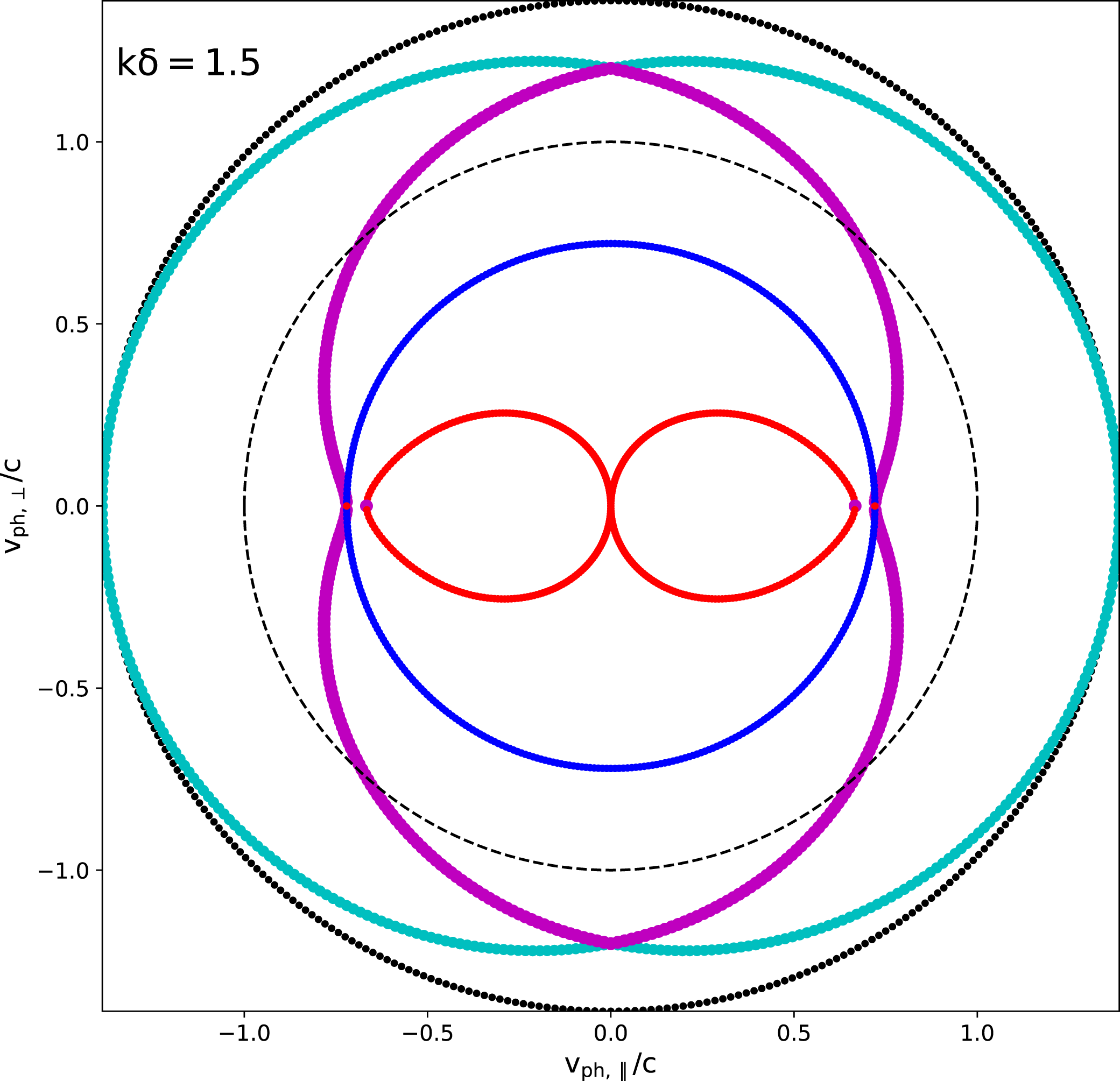
Figure 2. A representative phase diagram of all 5 wave modes for all angles, at fixed wavenumber
![]() $\bar{k}=1.5$
. The strict ordering of wave frequencies for all angles
$\bar{k}=1.5$
. The strict ordering of wave frequencies for all angles
![]() $0<\unicode[STIX]{x1D717}<\unicode[STIX]{x03C0}/2$
ensures these diagrams to be nested. At the chosen wavenumber, the modified electrostatic
$0<\unicode[STIX]{x1D717}<\unicode[STIX]{x03C0}/2$
ensures these diagrams to be nested. At the chosen wavenumber, the modified electrostatic
![]() $\unicode[STIX]{x1D714}_{\text{M}}$
(purple) and the electromagnetic O branch
$\unicode[STIX]{x1D714}_{\text{M}}$
(purple) and the electromagnetic O branch
![]() $\unicode[STIX]{x1D714}_{\text{O}}$
(cyan) coincide at perpendicular orientation, and for larger
$\unicode[STIX]{x1D714}_{\text{O}}$
(cyan) coincide at perpendicular orientation, and for larger
![]() $k$
they will have exchanged labels for this orientation. Such an exchange already occurred for parallel orientation between the red (
$k$
they will have exchanged labels for this orientation. Such an exchange already occurred for parallel orientation between the red (
![]() $\unicode[STIX]{x1D714}_{\text{A}}$
) and purple (
$\unicode[STIX]{x1D714}_{\text{A}}$
) and purple (
![]() $\unicode[STIX]{x1D714}_{\text{M}}$
) branch. The dashed circle indicates the light speed. An animation of this variation with wavenumber is provided as supplementary material in the movie Phasediagram.mp4.
$\unicode[STIX]{x1D714}_{\text{M}}$
) branch. The dashed circle indicates the light speed. An animation of this variation with wavenumber is provided as supplementary material in the movie Phasediagram.mp4.
3.3 Phase and group speed diagrams
We now present the complete phase and group speed diagrams, collecting all information of the various wave types for all angles and wavenumbers. Figure 2 shows a representative phase diagram for the case
![]() $E=1.5$
, earlier shown in dispersion diagram view in figure 1. Animating this diagram for varying wavenumber
$E=1.5$
, earlier shown in dispersion diagram view in figure 1. Animating this diagram for varying wavenumber
![]() $k$
shows clearly how the branch exchange witnessed at exactly parallel or perpendicular orientation occurs when the phase diagrams of two wave modes suddenly coincide at specific
$k$
shows clearly how the branch exchange witnessed at exactly parallel or perpendicular orientation occurs when the phase diagrams of two wave modes suddenly coincide at specific
![]() $k$
-values. The diagram shown is for a
$k$
-values. The diagram shown is for a
![]() $k$
value that exactly demonstrates this coincidence of branches at perpendicular orientation (along the central vertical in the figure). Exchange of wave mode types at parallel orientation (along the central horizontal in the figure) already switched an
$k$
value that exactly demonstrates this coincidence of branches at perpendicular orientation (along the central vertical in the figure). Exchange of wave mode types at parallel orientation (along the central horizontal in the figure) already switched an
![]() $\unicode[STIX]{x1D714}_{\text{A}}$
with an
$\unicode[STIX]{x1D714}_{\text{A}}$
with an
![]() $\unicode[STIX]{x1D714}_{\text{M}}$
mode (hence the purple dots on the red branch, and the red dots on the purple branch). It is to be noted that these phase diagrams are different from the ones usually shown as wave normal surfaces in the CMA view: we plot
$\unicode[STIX]{x1D714}_{\text{M}}$
mode (hence the purple dots on the red branch, and the red dots on the purple branch). It is to be noted that these phase diagrams are different from the ones usually shown as wave normal surfaces in the CMA view: we plot
![]() $[\unicode[STIX]{x1D714}/kc](\unicode[STIX]{x1D717})$
for fixed
$[\unicode[STIX]{x1D714}/kc](\unicode[STIX]{x1D717})$
for fixed
![]() $k$
-value, accounting for all 5 wave modes, textbook treatments plot
$k$
-value, accounting for all 5 wave modes, textbook treatments plot
![]() $[\unicode[STIX]{x1D714}/kc](\unicode[STIX]{x1D717})$
for fixed frequency
$[\unicode[STIX]{x1D714}/kc](\unicode[STIX]{x1D717})$
for fixed frequency
![]() $\unicode[STIX]{x1D714}$
, and hence mix information from varying wavenumbers (as horizontal intersections at fixed
$\unicode[STIX]{x1D714}$
, and hence mix information from varying wavenumbers (as horizontal intersections at fixed
![]() $\unicode[STIX]{x1D714}$
in dispersion views of figure 1 show the
$\unicode[STIX]{x1D714}$
in dispersion views of figure 1 show the
![]() $k$
values to change with angle
$k$
values to change with angle
![]() $\unicode[STIX]{x1D717}$
). The point to note is that
$\unicode[STIX]{x1D717}$
). The point to note is that
![]() $k(\unicode[STIX]{x1D714},\unicode[STIX]{x1D717})$
, and (2.1) allows a maximal 2 modes at fixed
$k(\unicode[STIX]{x1D714},\unicode[STIX]{x1D717})$
, and (2.1) allows a maximal 2 modes at fixed
![]() $\unicode[STIX]{x1D714}$
, while we emphasize one has exactly 5 modes for every real
$\unicode[STIX]{x1D714}$
, while we emphasize one has exactly 5 modes for every real
![]() $k$
. Note that superluminal phase speeds are encountered for solutions
$k$
. Note that superluminal phase speeds are encountered for solutions
![]() $\unicode[STIX]{x1D714}(k)$
above the dashed lines in figure 1, or equivalently outside the dashed circle in figure 2. Animated views for figure 1 are in the movie entitled DispersionRelation.mp4, and for figure 2 in the movie entitled
Phasediagram.mp4.
$\unicode[STIX]{x1D714}(k)$
above the dashed lines in figure 1, or equivalently outside the dashed circle in figure 2. Animated views for figure 1 are in the movie entitled DispersionRelation.mp4, and for figure 2 in the movie entitled
Phasediagram.mp4.

Figure 3. Representative group diagrams showing all 5 wave modes for all angles, at fixed wavenumbers
![]() $\bar{k}=1$
and 2 (a,b). The dashed circle indicates light speed. An animation of this variation with
$\bar{k}=1$
and 2 (a,b). The dashed circle indicates light speed. An animation of this variation with
![]() $\bar{k}$
is provided as supplementary material in the movie Groupdiagram.mp4.
$\bar{k}$
is provided as supplementary material in the movie Groupdiagram.mp4.
The group speed diagrams for all 5 wave modes can also be computed for every wavenumber
![]() $k$
. These diagrams directly enrich the well-known Friedrich diagrams for MHD (Goedbloed & Poedts Reference Goedbloed and Poedts2004), which visually display the extreme anisotropic wave behaviour of slow, Alfvén and fast modes at large wavelengths, low frequencies. In the cold pair plasma case, the slow pair is marginal, but Alfvén and fast remain, as in (3.4)–(3.2). Figure 3 shows the complete group diagram for
$k$
. These diagrams directly enrich the well-known Friedrich diagrams for MHD (Goedbloed & Poedts Reference Goedbloed and Poedts2004), which visually display the extreme anisotropic wave behaviour of slow, Alfvén and fast modes at large wavelengths, low frequencies. In the cold pair plasma case, the slow pair is marginal, but Alfvén and fast remain, as in (3.4)–(3.2). Figure 3 shows the complete group diagram for
![]() $E=1.5$
, at
$E=1.5$
, at
![]() $k=1$
and
$k=1$
and
![]() $k=2$
. The true complexity of the variation with wavenumber can only be appreciated in animated views (provided as supplementary material in the movie entitle Groupdiagram.mp4), but they correspond to the formulae in (3.2)–(3.3) (with limits as in (3.4)–(3.8)). The animation shows the intricate reshaping of the group speed curves, especially near the special values where branches cross (i.e. at
$k=2$
. The true complexity of the variation with wavenumber can only be appreciated in animated views (provided as supplementary material in the movie entitle Groupdiagram.mp4), but they correspond to the formulae in (3.2)–(3.3) (with limits as in (3.4)–(3.8)). The animation shows the intricate reshaping of the group speed curves, especially near the special values where branches cross (i.e. at
![]() $k^{2}=E^{2}$
and at
$k^{2}=E^{2}$
and at
![]() $k^{2}=E^{2}/(E^{2}-1)$
when
$k^{2}=E^{2}/(E^{2}-1)$
when
![]() $E>1$
). For all three wave modes
$E>1$
). For all three wave modes
![]() $\unicode[STIX]{x1D714}_{\text{A}}$
,
$\unicode[STIX]{x1D714}_{\text{A}}$
,
![]() $\unicode[STIX]{x1D714}_{\text{M}}$
and
$\unicode[STIX]{x1D714}_{\text{M}}$
and
![]() $\unicode[STIX]{x1D714}_{\text{O}}$
which demonstrate coupling and exchange of mode limits at small wavelengths, the energy flow as quantified through these group diagrams is strongly anisotropic, and a proper visualization of their variation with wavenumber
$\unicode[STIX]{x1D714}_{\text{O}}$
which demonstrate coupling and exchange of mode limits at small wavelengths, the energy flow as quantified through these group diagrams is strongly anisotropic, and a proper visualization of their variation with wavenumber
![]() $k$
requires us to pay full attention to sudden variations with angle
$k$
requires us to pay full attention to sudden variations with angle
![]() $\unicode[STIX]{x1D717}$
, especially at near-parallel or near-perpendicular orientations. Note that, as physically required, all group speeds are always found within the light circle. Finally, limit cases can now be fully understood as special instances of these 5 wave mode pairs: the unmagnetized (
$\unicode[STIX]{x1D717}$
, especially at near-parallel or near-perpendicular orientations. Note that, as physically required, all group speeds are always found within the light circle. Finally, limit cases can now be fully understood as special instances of these 5 wave mode pairs: the unmagnetized (
![]() $E=0$
) cold pair plasma leaves
$E=0$
) cold pair plasma leaves
![]() $\unicode[STIX]{x1D714}_{\text{M}}=1$
as electrostatic modes, both electromagnetic
$\unicode[STIX]{x1D714}_{\text{M}}=1$
as electrostatic modes, both electromagnetic
![]() $\unicode[STIX]{x1D714}_{\text{O,X}}$
pairs coincide on
$\unicode[STIX]{x1D714}_{\text{O,X}}$
pairs coincide on
![]() $\unicode[STIX]{x1D714}^{2}=1+k^{2}$
, while Alfvénic and fast branches become marginal. The strongly magnetized
$\unicode[STIX]{x1D714}^{2}=1+k^{2}$
, while Alfvénic and fast branches become marginal. The strongly magnetized
![]() $E\rightarrow \infty$
case, moves the electromagnetic waves to infinite frequencies, and keeps the
$E\rightarrow \infty$
case, moves the electromagnetic waves to infinite frequencies, and keeps the
![]() $\unicode[STIX]{x1D714}_{\text{M}}$
,
$\unicode[STIX]{x1D714}_{\text{M}}$
,
![]() $\unicode[STIX]{x1D714}_{\text{F}}$
and
$\unicode[STIX]{x1D714}_{\text{F}}$
and
![]() $\unicode[STIX]{x1D714}_{\text{A}}$
branches.
$\unicode[STIX]{x1D714}_{\text{A}}$
branches.
4 Conclusions
Our treatment of all wave mode pairs in a cold pair plasma provides, for the first time, a complete categorization of all wave anisotropies inherent in cold pair plasmas. This is best appreciated from our quantification of the phase and group speed for all 5 mode pairs, at all wavenumbers and angles (i.e. our equations (3.2)–(3.3) and the animations provided with figures 2 and 3). Rather than working in terms of the breaking index
![]() $n^{2}$
, our starting point was the general twelfth-order dispersion relation for warm plasmas, containing six mode pair solutions (e.g. Goedbloed & Poedts Reference Goedbloed and Poedts2004), which reduce to 5 non-trivial
$n^{2}$
, our starting point was the general twelfth-order dispersion relation for warm plasmas, containing six mode pair solutions (e.g. Goedbloed & Poedts Reference Goedbloed and Poedts2004), which reduce to 5 non-trivial
![]() $\unicode[STIX]{x1D714}^{2}$
solutions in the cold limit. A quantification of the mode polarizations should best employ the 6 variables used there to obtain a fully symmetric matrix representation. A completely similar treatment can be done for cold electron–ion cases (where two parameters will enter,
$\unicode[STIX]{x1D714}^{2}$
solutions in the cold limit. A quantification of the mode polarizations should best employ the 6 variables used there to obtain a fully symmetric matrix representation. A completely similar treatment can be done for cold electron–ion cases (where two parameters will enter,
![]() $E$
and its counterpart for ions
$E$
and its counterpart for ions
![]() $I=\unicode[STIX]{x1D6FA}_{i}/\unicode[STIX]{x1D714}_{p}$
), or for warm plasmas (where also the thermal speeds of the species come in). Still, the polynomial form of the dispersion relation renders computing all six
$I=\unicode[STIX]{x1D6FA}_{i}/\unicode[STIX]{x1D714}_{p}$
), or for warm plasmas (where also the thermal speeds of the species come in). Still, the polynomial form of the dispersion relation renders computing all six
![]() $\unicode[STIX]{x1D714}^{2}$
pairs for warm plasmas fairly trivial, and the quantification of group speeds along all six
$\unicode[STIX]{x1D714}^{2}$
pairs for warm plasmas fairly trivial, and the quantification of group speeds along all six
![]() $\unicode[STIX]{x1D714}(k,\unicode[STIX]{x1D717})$
branches becomes possible. For warm plasmas, avoided crossings between several branches may show up at intermediate angles, instead of at the extremes of purely parallel or perpendicular orientations as illustrated here. The slow MHD wave will form the extra ingredient to categorize all 6 wave modes in warm plasmas, starting from their ordering in frequency as found at large wavelengths. Avoided crossings will cause more intricate reorderings of branches, as connectivity to small wavelength limits at resonances or electromagnetic limits can change with angle
$\unicode[STIX]{x1D714}(k,\unicode[STIX]{x1D717})$
branches becomes possible. For warm plasmas, avoided crossings between several branches may show up at intermediate angles, instead of at the extremes of purely parallel or perpendicular orientations as illustrated here. The slow MHD wave will form the extra ingredient to categorize all 6 wave modes in warm plasmas, starting from their ordering in frequency as found at large wavelengths. Avoided crossings will cause more intricate reorderings of branches, as connectivity to small wavelength limits at resonances or electromagnetic limits can change with angle
![]() $\unicode[STIX]{x1D717}$
.
$\unicode[STIX]{x1D717}$
.
Although our discussion is based on an ideal two-fluid viewpoint, this forms the basis of more realistic kinetic treatments which all employ the dielectric tensor formulation. A useful intermediate step would be to incorporate collisional effects, such as done in Stewart & Laing (Reference Stewart and Laing1992) or in Goedbloed & Poedts (Reference Goedbloed and Poedts2004). This would already allow for wave damping, and in warm plasmas, handling pressure anisotropy will open the route to firehose instabilities. Allowing for relative streaming of both species will break the symmetry of the forward–backward pairs in the fluid limit, a phenomenon known to introduce fascinating complexities to the MHD wave part of the spectrum (Goedbloed, Keppens & Poedts Reference Goedbloed, Keppens and Poedts2010, Reference Goedbloed, Keppens and Poedts2019).
Acknowledgements
This research was supported by the KU Leuven (GOA/2015-014). R.K. thanks Yunnan University and C. Xia for kind hospitality during his sabbatical stay.
Supplementary movies
Supplementary movies are available at https://doi.org/10.1017/S0022377819000102.