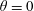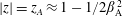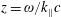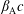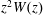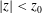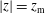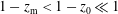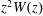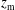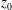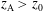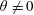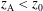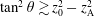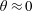1 Introduction
The mechanism by which pulsar radio emission is generated remains controversial. Several different mechanisms continue to attract supporters and critics, including coherent curvature emission (CCE), relativistic plasma emission (RPE), anomalous Doppler emission (ADE), linear acceleration emission (LAE) and free-electron maser emission (FEM). Two of these (RPE and ADE) depend intrinsically on the wave dispersion in the ‘pulsar plasma’ which we define to be a one-dimensional (1-D), electron–positron plasma, streaming outward at a relativistic velocity
![]() $\unicode[STIX]{x1D6FD}_{\text{s}}c$
, where
$\unicode[STIX]{x1D6FD}_{\text{s}}c$
, where
![]() $\unicode[STIX]{x1D6FD}_{\text{s}}$
is the streaming speed,
$\unicode[STIX]{x1D6FD}_{\text{s}}$
is the streaming speed,
![]() $c$
is the speed of light, with streaming Lorentz factor
$c$
is the speed of light, with streaming Lorentz factor
![]() $\unicode[STIX]{x1D6FE}_{\text{s}}=(1-\unicode[STIX]{x1D6FD}_{\text{s}}^{2})^{-1/2}\gg 1$
, and with an intrinsically relativistic spread in Lorentz factors,
$\unicode[STIX]{x1D6FE}_{\text{s}}=(1-\unicode[STIX]{x1D6FD}_{\text{s}}^{2})^{-1/2}\gg 1$
, and with an intrinsically relativistic spread in Lorentz factors,
![]() $\langle \unicode[STIX]{x1D6FE}\rangle \gg 1$
, where
$\langle \unicode[STIX]{x1D6FE}\rangle \gg 1$
, where
![]() $\langle \cdots \rangle$
denote an average, in the rest frame of the streaming plasma. Wave dispersion in such a pulsar plasma has major differences from wave dispersion in a conventional plasma, due to the extreme anisotropy, in the form of 1-D distributions, the absence of ions, the highly relativistic energies of the bulk of the particles and the superstrong magnetic field. For example, all waves in a pulsar plasma have phase speeds very close to or above the speed of light, and the longitudinal waves exist only for propagation parallel to the magnetic field.
$\langle \cdots \rangle$
denote an average, in the rest frame of the streaming plasma. Wave dispersion in such a pulsar plasma has major differences from wave dispersion in a conventional plasma, due to the extreme anisotropy, in the form of 1-D distributions, the absence of ions, the highly relativistic energies of the bulk of the particles and the superstrong magnetic field. For example, all waves in a pulsar plasma have phase speeds very close to or above the speed of light, and the longitudinal waves exist only for propagation parallel to the magnetic field.
Renewed interest in RPE has been stimulated by a recent argument in favour of a ‘beam-driven’ form of RPE: Eilek & Hankins (Reference Eilek and Hankins2016) argued that RPE is the only one of the suggested mechanisms that can plausibly account for nanoshots from the Crab pulsar. Specifically, the form of RPE invoked by Eilek & Hankins (Reference Eilek and Hankins2016) involves beam-driven Langmuir-like waves, which are assumed to build up to a very high level in localized regions in the pulsar magnetosphere through a mechanism suggested by Weatherall (Reference Weatherall1997, Reference Weatherall1998). This argument has potentially wider implications: it is intrinsically unlikely that the emission mechanism in nanoshots is unrelated to other pulsar radio emission and hence, if the case for RPE operating in nanoshots is accepted, this would provide a strong argument for RPE being the generic mechanism for pulsar radio emission. In most forms of RPE (Suvorov & Chugunov Reference Suvorov and Chugunov1973, Reference Suvorov and Chugunov1975; Hardee & Rose Reference Hardee and Rose1976, Reference Hardee and Rose1978; Hinata Reference Hinata1976a ,Reference Hinata b ; Benford & Buschauer Reference Benford and Buschauer1977; Lominadze, Mikhaǐlovskiǐ & Sagdeev Reference Lominadze, Mikhaǐlovskiǐ and Sagdeev1979; Lominadze & Pataraya Reference Lominadze and Pataraya1982; Asseo, Pellat & Sol Reference Asseo, Pellat and Sol1983; Egorenkov, Lominadze & Mamradze Reference Egorenkov, Lominadze and Mamradze1983; Lyubarskii Reference Lyubarskii1992; Asseo Reference Asseo1993, Reference Asseo1995; Weatherall Reference Weatherall1994), including the form proposed for nanoshots, it is assumed that Langmuir-like waves exist in the pulsar plasma, with properties similar to Langmuir waves in a non-relativistic plasma, but there are no such waves in a pulsar plasma. Any growing wave must be in a specific wave mode of the pulsar plasma.
In this paper, and in two accompanying papers (Rafat, Melrose & Mastrano (Reference Rafat, Melrose and Mastrano2019a
,Reference Rafat, Melrose and Mastrano
b
) referred to as Parts 2 and 3), we discuss wave dispersion and beam-driven instabilities in pulsar plasma with the objective of providing a systematic description of the underlying plasma theory needed in a critical discussion of the beam-driven instabilities invoked in RPE and CCE. Our main purpose in this paper is to describe wave dispersion in a plasma with the properties that we postulate here for a pulsar plasma in its rest frame. In particular we emphasize the importance of the relativistic spread
![]() $\langle \unicode[STIX]{x1D6FE}\rangle \gg 1$
. In all three papers we assume that every particle distribution is a one-dimensional Jüttner distribution, which is of the form
$\langle \unicode[STIX]{x1D6FE}\rangle \gg 1$
. In all three papers we assume that every particle distribution is a one-dimensional Jüttner distribution, which is of the form
![]() $g(u)\propto \exp (-\unicode[STIX]{x1D70C}\unicode[STIX]{x1D6FE})$
, with
$g(u)\propto \exp (-\unicode[STIX]{x1D70C}\unicode[STIX]{x1D6FE})$
, with
![]() $\unicode[STIX]{x1D70C}$
the inverse temperature in units of the rest energy of the electron, and with
$\unicode[STIX]{x1D70C}$
the inverse temperature in units of the rest energy of the electron, and with
![]() $u=\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FD}$
the 4-speed. Numerical models suggest that the pair cascade results in broad particle distributions (Hibschman & Arons Reference Hibschman and Arons2001; Arendt & Eilek Reference Arendt and Eilek2002; Medin & Lai Reference Medin and Lai2010; Timokhin & Arons Reference Timokhin and Arons2013), which have been described as Jüttner-like (e.g. Arendt & Eilek Reference Arendt and Eilek2002).
$u=\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FD}$
the 4-speed. Numerical models suggest that the pair cascade results in broad particle distributions (Hibschman & Arons Reference Hibschman and Arons2001; Arendt & Eilek Reference Arendt and Eilek2002; Medin & Lai Reference Medin and Lai2010; Timokhin & Arons Reference Timokhin and Arons2013), which have been described as Jüttner-like (e.g. Arendt & Eilek Reference Arendt and Eilek2002).
A Jüttner distribution should be regarded as the default choice for the distribution function for the particles in a pulsar plasma and in other relativistic astrophysical pair plasmas. A Jüttner distribution (Jüttner Reference Jüttner1911; Synge Reference Synge1957; Wright & Hadley Reference Wright and Hadley1975) is the relativistic generalization of a thermal (or Maxwellian) distribution. We suggest that a pulsar plasma should be regarded as analogous to most non-relativistic astrophysical plasmas in the sense that there is a ‘background’ distribution that is thermal (Maxwellian or Jüttner) with suprathermal tails and other non-thermal features regarded as complementary distributions or as modifications to this ‘background’ distribution. The wave dispersion is assumed to be determined primarily by the ‘background’ with instabilities attributed to non-thermal features.
Indirect evidence for a Jüttner distribution follows from numerical calculations, particularly particle-in-cell calculations, from which the form of the distribution function can be inferred. As already noted, the results of such calculations for pair creation in a pulsar plasma suggest a 1-D Jüttner distribution. Another astrophysical problem concerns the propagation of a shock into an electron–positron plasma, and again the resulting distribution of the post-shock pair plasma is consistent with a Jüttner distribution (e.g. Gallant et al.
Reference Gallant, Hoshino, Langdon, Arons and Max1992; Sironi & Spitkovsky Reference Sironi and Spitkovsky2009; Iwamoto et al.
Reference Iwamoto, Amano, Hoshino and Matsumoto2017). While such calculations do not provide compelling evidence for a Jüttner distribution, they do support the suggestion that the default choice should be a Jüttner distribution. One needs a specific reason for choosing any other distribution for a relativistic pair plasma in an astrophysical context. The implications of this default assumption are more important for streaming distributions (Part 2) than for the non-streaming distribution considered in the present paper, where the main effect is the large intrinsic spread in Lorentz factors,
![]() $\langle \unicode[STIX]{x1D6FE}\rangle \approx 1/\unicode[STIX]{x1D70C}\gg 1$
for the highly relativistic case,
$\langle \unicode[STIX]{x1D6FE}\rangle \approx 1/\unicode[STIX]{x1D70C}\gg 1$
for the highly relativistic case,
![]() $\unicode[STIX]{x1D70C}\ll 1$
, of interest here. Arendt & Eilek (Reference Arendt and Eilek2002) suggested a Jüttner distribution with
$\unicode[STIX]{x1D70C}\ll 1$
, of interest here. Arendt & Eilek (Reference Arendt and Eilek2002) suggested a Jüttner distribution with
![]() $\unicode[STIX]{x1D70C}\approx 1$
and
$\unicode[STIX]{x1D70C}\approx 1$
and
![]() $\unicode[STIX]{x1D6FE}_{\text{s}}=10^{2}{-}10^{3}$
as being relevant to pulsars. Such numerical models apply in local regions where pair cascades occur, and it is plausible that many such local regions contribute to the distribution function of the outwardly streaming pulsar plasma of interest here. A distribution consisting of many such local distributions has a wide spread in Lorentz factor, and we suggest that this may be modelled by a Jüttner distribution with a smaller value of
$\unicode[STIX]{x1D6FE}_{\text{s}}=10^{2}{-}10^{3}$
as being relevant to pulsars. Such numerical models apply in local regions where pair cascades occur, and it is plausible that many such local regions contribute to the distribution function of the outwardly streaming pulsar plasma of interest here. A distribution consisting of many such local distributions has a wide spread in Lorentz factor, and we suggest that this may be modelled by a Jüttner distribution with a smaller value of
![]() $\unicode[STIX]{x1D70C}$
. We discuss both the case
$\unicode[STIX]{x1D70C}$
. We discuss both the case
![]() $\unicode[STIX]{x1D70C}=1$
, and also the case
$\unicode[STIX]{x1D70C}=1$
, and also the case
![]() $\unicode[STIX]{x1D70C}\ll 1$
. We find that the wave dispersion for
$\unicode[STIX]{x1D70C}\ll 1$
. We find that the wave dispersion for
![]() $\unicode[STIX]{x1D70C}=1$
, is more closely analogous to the highly relativistic case
$\unicode[STIX]{x1D70C}=1$
, is more closely analogous to the highly relativistic case
![]() $\unicode[STIX]{x1D70C}\ll 1$
than to the non-relativistic case
$\unicode[STIX]{x1D70C}\ll 1$
than to the non-relativistic case
![]() $\unicode[STIX]{x1D70C}\gg 1$
.
$\unicode[STIX]{x1D70C}\gg 1$
.
There are three wave modes in a pulsar plasma, labelled here as X, L and A for parallel propagation and as X, O and Alfvén for oblique propagation. It is convenient to choose the phase speed
![]() $z=\unicode[STIX]{x1D714}/k_{\Vert }c$
as the independent variable, and to introduce two plasma parameters: the plasma frequency,
$z=\unicode[STIX]{x1D714}/k_{\Vert }c$
as the independent variable, and to introduce two plasma parameters: the plasma frequency,
![]() $\unicode[STIX]{x1D714}_{\text{p}}$
, defined without including any Lorentz factors, and
$\unicode[STIX]{x1D714}_{\text{p}}$
, defined without including any Lorentz factors, and
![]() $\unicode[STIX]{x1D6FD}_{\text{A}}$
which is such that
$\unicode[STIX]{x1D6FD}_{\text{A}}$
which is such that
![]() $\unicode[STIX]{x1D6FD}_{\text{A}}c$
is the Alfvén velocity, as conventionally defined, with
$\unicode[STIX]{x1D6FD}_{\text{A}}c$
is the Alfvén velocity, as conventionally defined, with
![]() $\unicode[STIX]{x1D6FD}_{\text{A}}\gg 1$
in a pulsar magnetosphere. For parallel propagation, the X and A modes are degenerate with dispersion relation
$\unicode[STIX]{x1D6FD}_{\text{A}}\gg 1$
in a pulsar magnetosphere. For parallel propagation, the X and A modes are degenerate with dispersion relation
![]() $z=z_{\text{A}}$
, with
$z=z_{\text{A}}$
, with
![]() $z_{\text{A}}\approx \unicode[STIX]{x1D6FD}_{\text{A}}/(1+\unicode[STIX]{x1D6FD}_{\text{A}}^{2})^{1/2}$
. The L mode has dispersion relation
$z_{\text{A}}\approx \unicode[STIX]{x1D6FD}_{\text{A}}/(1+\unicode[STIX]{x1D6FD}_{\text{A}}^{2})^{1/2}$
. The L mode has dispersion relation
![]() $\unicode[STIX]{x1D714}=\unicode[STIX]{x1D714}_{\text{L}}(z)$
, with
$\unicode[STIX]{x1D714}=\unicode[STIX]{x1D714}_{\text{L}}(z)$
, with
![]() $\unicode[STIX]{x1D714}_{\text{L}}^{2}(z)=\unicode[STIX]{x1D714}_{\text{p}}^{2}z^{2}W(z)$
, where
$\unicode[STIX]{x1D714}_{\text{L}}^{2}(z)=\unicode[STIX]{x1D714}_{\text{p}}^{2}z^{2}W(z)$
, where
![]() $z^{2}W(z)$
is a relativistic plasma dispersion function (RPDF), with
$z^{2}W(z)$
is a relativistic plasma dispersion function (RPDF), with
![]() $W(z)$
defined in (A 8).
$W(z)$
defined in (A 8).
RPE may be regarded as a pulsar counterpart of conventional plasma emission, for example, in solar radio bursts (e.g. Melrose Reference Melrose1986, p. 94). Plasma emission involves at least two stages, with the first stage being an instability that generates turbulence in Langmuir waves, and another stage involving partial conversion of energy in this turbulence into escaping radio waves. Two difficulties were recognized in early discussions of RPE. First, the growth rate for various suggested instabilities in the first stage is too slow to be effective, and ways in which this might be overcome were proposed and explored (Usov Reference Usov1987; Ursov & Usov Reference Ursov and Usov1988; Asseo & Melikidze Reference Asseo and Melikidze1998; Gedalin, Gruman & Melrose Reference Gedalin, Gruman and Melrose2002). Second, the conversion mechanism into escaping radiation is problematic, and was referred to as a ‘bottle-neck’ by Usov (Reference Usov, Kramer, Wex and Wielebinski2000). Here we are concerned with a third difficulty with RPE: the existence of ‘Langmuir-like’ waves that can be generated through a beam instability. This difficulty is obscured in most discussions of RPE through over-simplified or implicit assumptions about the wave dispersion. Examples include the assumption that the plasma is cold or non-relativistic (in its rest frame), or that the waves have non-relativistic phase and/or group speeds. We argue that in a relativistic pair plasma, with
![]() $\unicode[STIX]{x1D70C}\lesssim 1$
, all waves have relativistic phase speeds, calling into question the possibility of beam-driven ‘Langmuir-like’ waves in pulsar plasma. We conclude that, like other proposed emission mechanisms, beam-driven RPE encounters seemingly overwhelming difficulties as the generic pulsar radio emission mechanism.
$\unicode[STIX]{x1D70C}\lesssim 1$
, all waves have relativistic phase speeds, calling into question the possibility of beam-driven ‘Langmuir-like’ waves in pulsar plasma. We conclude that, like other proposed emission mechanisms, beam-driven RPE encounters seemingly overwhelming difficulties as the generic pulsar radio emission mechanism.
In § 2 we present a general theory for wave dispersion in a pulsar plasma, and in § 3 we summarize the properties of the RPDF. In § 4 we describe the wave dispersion in cases where the spread
![]() $\langle \unicode[STIX]{x1D6FE}\rangle$
is neglected (‘cold’ plasma,
$\langle \unicode[STIX]{x1D6FE}\rangle$
is neglected (‘cold’ plasma,
![]() $\langle \unicode[STIX]{x1D6FE}\rangle =1$
), where it is non-relativistic (
$\langle \unicode[STIX]{x1D6FE}\rangle =1$
), where it is non-relativistic (
![]() $\langle \unicode[STIX]{x1D6FE}\rangle -1\ll 1$
), and where relativistic effects are important (
$\langle \unicode[STIX]{x1D6FE}\rangle -1\ll 1$
), and where relativistic effects are important (
![]() $\langle \unicode[STIX]{x1D6FE}\rangle \gtrsim 1$
). In § 5 we derive results for the wave dispersion in the plasma rest frame for
$\langle \unicode[STIX]{x1D6FE}\rangle \gtrsim 1$
). In § 5 we derive results for the wave dispersion in the plasma rest frame for
![]() $\langle \unicode[STIX]{x1D6FE}\rangle \gg 1$
. In § 6 we discuss the properties of the L mode in more detail, emphasizing the reasons why the mode should not be regarded as ‘Langmuir-like’. We discuss our results and summarize our conclusions in § 7. A list of the notation used is included in table 3.
$\langle \unicode[STIX]{x1D6FE}\rangle \gg 1$
. In § 6 we discuss the properties of the L mode in more detail, emphasizing the reasons why the mode should not be regarded as ‘Langmuir-like’. We discuss our results and summarize our conclusions in § 7. A list of the notation used is included in table 3.
2 Wave dispersion in pulsar plasma
In this section we discuss wave dispersion in a pulsar plasma based on the approach presented by Melrose & Gedalin (Reference Melrose and Gedalin1999) and Melrose et al. (Reference Melrose, Gedalin, Kennett and Fletcher1999). We present our detailed calculations and assumptions in appendix A.
2.1 Wave dispersion in two frames
Dispersion in any plasma may be described by its dielectric tensor
![]() $\unicode[STIX]{x1D612}_{ij}(\unicode[STIX]{x1D714},\boldsymbol{k})$
and the wave equation written in the form
$\unicode[STIX]{x1D612}_{ij}(\unicode[STIX]{x1D714},\boldsymbol{k})$
and the wave equation written in the form
![]() $\unicode[STIX]{x1D6EC}_{ij}(\unicode[STIX]{x1D714},\boldsymbol{k})e_{j}=0$
, with
$\unicode[STIX]{x1D6EC}_{ij}(\unicode[STIX]{x1D714},\boldsymbol{k})e_{j}=0$
, with
![]() $\boldsymbol{e}$
the polarization vector and with wave equation tensor
$\boldsymbol{e}$
the polarization vector and with wave equation tensor
where
![]() $\unicode[STIX]{x1D6FF}_{ij}$
is the Kronecker delta. The dispersion equation is given by setting the determinant of
$\unicode[STIX]{x1D6FF}_{ij}$
is the Kronecker delta. The dispersion equation is given by setting the determinant of
![]() $\unicode[STIX]{x1D6EC}_{ij}$
to zero. In appendix A we derive the non-zero components of
$\unicode[STIX]{x1D6EC}_{ij}$
to zero. In appendix A we derive the non-zero components of
![]() $\unicode[STIX]{x1D6EC}_{ij}(\unicode[STIX]{x1D714},\boldsymbol{k})$
as given by (A 10), making the low-frequency approximation in § A.2.1 and the non-gyrotropic approximation in § A.2.2. The dispersion equation then may be written as,
$\unicode[STIX]{x1D6EC}_{ij}(\unicode[STIX]{x1D714},\boldsymbol{k})$
as given by (A 10), making the low-frequency approximation in § A.2.1 and the non-gyrotropic approximation in § A.2.2. The dispersion equation then may be written as,
![]() $\unicode[STIX]{x1D6EC}_{ij}(\unicode[STIX]{x1D714},\boldsymbol{k})\rightarrow \unicode[STIX]{x1D6EC}_{ij}$
,
$\unicode[STIX]{x1D6EC}_{ij}(\unicode[STIX]{x1D714},\boldsymbol{k})\rightarrow \unicode[STIX]{x1D6EC}_{ij}$
,
The dispersion relation for any specific wave mode is a specific solution of the dispersion (2.2). Here we derive and discuss the wave properties in the rest frame of the plasma; we discuss the wave properties Lorentz transformed to the pulsar frame in Part 2. We argue for the use of a Jüttner distribution to describe a pulsar plasma (Arendt & Eilek Reference Arendt and Eilek2002), which is an even function of
![]() $\unicode[STIX]{x1D6FD}$
in the plasma rest frame. For a distribution that is an even function of
$\unicode[STIX]{x1D6FD}$
in the plasma rest frame. For a distribution that is an even function of
![]() $\unicode[STIX]{x1D6FD}$
the non-zero components of
$\unicode[STIX]{x1D6FD}$
the non-zero components of
![]() $\unicode[STIX]{x1D6EC}_{ij}$
are given by (A 11).
$\unicode[STIX]{x1D6EC}_{ij}$
are given by (A 11).
For parallel propagation,
![]() $\unicode[STIX]{x1D703}=0$
, we have
$\unicode[STIX]{x1D703}=0$
, we have
![]() $\unicode[STIX]{x1D6EC}_{13}=0$
so that the solutions of (2.2) are
$\unicode[STIX]{x1D6EC}_{13}=0$
so that the solutions of (2.2) are
![]() $\unicode[STIX]{x1D6EC}_{22}=0$
,
$\unicode[STIX]{x1D6EC}_{22}=0$
,
![]() $\unicode[STIX]{x1D6EC}_{11}=0$
and
$\unicode[STIX]{x1D6EC}_{11}=0$
and
![]() $\unicode[STIX]{x1D6EC}_{33}=0$
which give the dispersion equation for the parallel X mode, parallel Alfvén or A mode and the parallel longitudinal or L mode, respectively, with explicit expressions
$\unicode[STIX]{x1D6EC}_{33}=0$
which give the dispersion equation for the parallel X mode, parallel Alfvén or A mode and the parallel longitudinal or L mode, respectively, with explicit expressions
where
![]() $z_{\text{A}}$
is given in (A 11),
$z_{\text{A}}$
is given in (A 11),
![]() $\text{Re}W(z)$
denotes the real component of
$\text{Re}W(z)$
denotes the real component of
![]() $W(z)$
, with
$W(z)$
, with
![]() $W(z)$
defined in (A 8). For simplicity in writing we omit
$W(z)$
defined in (A 8). For simplicity in writing we omit
![]() $\text{Re}$
in the definition of
$\text{Re}$
in the definition of
![]() $\unicode[STIX]{x1D714}_{\text{L}}^{2}(z)$
. The parallel X and A modes are identical and may also be expressed as
$\unicode[STIX]{x1D714}_{\text{L}}^{2}(z)$
. The parallel X and A modes are identical and may also be expressed as
![]() $\unicode[STIX]{x1D714}^{2}=z_{\text{A}}^{2}c^{2}k_{\Vert }^{2}$
.
$\unicode[STIX]{x1D714}^{2}=z_{\text{A}}^{2}c^{2}k_{\Vert }^{2}$
.
For oblique propagation,
![]() $\unicode[STIX]{x1D703}\neq 0$
, the solution
$\unicode[STIX]{x1D703}\neq 0$
, the solution
![]() $\unicode[STIX]{x1D6EC}_{22}=0$
gives the oblique X mode,
$\unicode[STIX]{x1D6EC}_{22}=0$
gives the oblique X mode,
where
![]() $b$
is given in (A 11). The solution
$b$
is given in (A 11). The solution
![]() $\unicode[STIX]{x1D6EC}_{11}\unicode[STIX]{x1D6EC}_{33}-\unicode[STIX]{x1D6EC}_{13}^{2}=0$
gives the Alfvén and the O modes,
$\unicode[STIX]{x1D6EC}_{11}\unicode[STIX]{x1D6EC}_{33}-\unicode[STIX]{x1D6EC}_{13}^{2}=0$
gives the Alfvén and the O modes,
where
![]() $\unicode[STIX]{x1D714}_{\text{L}}(z)$
is given in (2.3). For
$\unicode[STIX]{x1D714}_{\text{L}}(z)$
is given in (2.3). For
![]() $\unicode[STIX]{x1D714}_{\text{L}}^{2}(z)>0$
, the O mode is given by (2.5) over
$\unicode[STIX]{x1D714}_{\text{L}}^{2}(z)>0$
, the O mode is given by (2.5) over
![]() $z_{\text{A}}^{2}+b\tan ^{2}\unicode[STIX]{x1D703}<z^{2}\leqslant \infty$
and the Alfvén mode is over
$z_{\text{A}}^{2}+b\tan ^{2}\unicode[STIX]{x1D703}<z^{2}\leqslant \infty$
and the Alfvén mode is over
![]() $z_{0}^{2}\leqslant z^{2}<z_{\text{A}}^{2}$
with
$z_{0}^{2}\leqslant z^{2}<z_{\text{A}}^{2}$
with
![]() $z_{0}$
such that
$z_{0}$
such that
![]() $\unicode[STIX]{x1D714}_{\text{L}}^{2}(z_{0})=0$
. The case
$\unicode[STIX]{x1D714}_{\text{L}}^{2}(z_{0})=0$
. The case
![]() $\unicode[STIX]{x1D714}_{\text{L}}^{2}(z)<0$
is more subtle and is discussed below.
$\unicode[STIX]{x1D714}_{\text{L}}^{2}(z)<0$
is more subtle and is discussed below.
The polarization vector
![]() $\boldsymbol{e}$
corresponding to a solution of
$\boldsymbol{e}$
corresponding to a solution of
![]() $\unicode[STIX]{x1D6EC}_{22}=0$
is along the 2-axis, which implies that the X mode is strictly transverse. Any solution of
$\unicode[STIX]{x1D6EC}_{22}=0$
is along the 2-axis, which implies that the X mode is strictly transverse. Any solution of
![]() $\unicode[STIX]{x1D6EC}_{11}\unicode[STIX]{x1D6EC}_{33}-\unicode[STIX]{x1D6EC}_{13}^{2}=0$
corresponds to a polarization vector,
$\unicode[STIX]{x1D6EC}_{11}\unicode[STIX]{x1D6EC}_{33}-\unicode[STIX]{x1D6EC}_{13}^{2}=0$
corresponds to a polarization vector,
![]() $\boldsymbol{e}$
, in the 1-3 plane with
$\boldsymbol{e}$
, in the 1-3 plane with
Longitudinal polarization corresponds to
![]() $\boldsymbol{e}=(\sin \unicode[STIX]{x1D703},0,\cos \unicode[STIX]{x1D703})$
, and the only strictly longitudinal waves are for parallel propagation,
$\boldsymbol{e}=(\sin \unicode[STIX]{x1D703},0,\cos \unicode[STIX]{x1D703})$
, and the only strictly longitudinal waves are for parallel propagation,
![]() $\sin \unicode[STIX]{x1D703}=0$
, satisfying the dispersion equation
$\sin \unicode[STIX]{x1D703}=0$
, satisfying the dispersion equation
![]() $\unicode[STIX]{x1D6EC}_{33}=0$
, which implies that the L mode is strictly longitudinal.
$\unicode[STIX]{x1D6EC}_{33}=0$
, which implies that the L mode is strictly longitudinal.
There are three modes present for either parallel propagation (parallel X, A and L modes) or oblique propagation (oblique X, Alfvén and O modes). In the rest frame of the plasma, each mode has a forward-propagating component,
![]() $z>0$
, and a backward-propagating component,
$z>0$
, and a backward-propagating component,
![]() $z<0$
. The backward-propagating portion is a mirror image of the forward-propagating one about
$z<0$
. The backward-propagating portion is a mirror image of the forward-propagating one about
![]() $z=0$
. We restrict our discussion to the forward-propagating solution from which the properties of the backward-propagating part can be readily inferred.
$z=0$
. We restrict our discussion to the forward-propagating solution from which the properties of the backward-propagating part can be readily inferred.
3 Relativistic plasma dispersion function
Wave dispersion in a non-relativistic plasma with Maxwellian distributions of particles may be described in terms of the well-known plasma dispersion function, which has both real and imaginary parts. As usually defined the real part determines the wave dispersion and the imaginary part determines damping of the waves due to resonant absorption. Wave dispersion in a pulsar plasma similarly involves the real and imaginary parts of the RPDF
![]() $z^{2}W(z)$
.
$z^{2}W(z)$
.
3.1 One-dimensional Jüttner distribution
Several different choices have been made for the distribution function of the electrons in a pulsar magnetosphere, including a power law (Kaplan & Tsytovich Reference Kaplan and Tsytovich1973, §17), a relativistically streaming Gaussian distribution (e.g. Egorenkov et al. Reference Egorenkov, Lominadze and Mamradze1983; Asseo & Melikidze Reference Asseo and Melikidze1998) and water-bag and bell distributions (Arons & Barnard Reference Arons and Barnard1986; Melrose & Gedalin Reference Melrose and Gedalin1999). Although the distribution function for the electrons and positrons in the rest frame of the plasma is not known, a relativistic thermal distribution is one approximate form suggested by numerical models for the cascade that generates the pair plasma (Hibschman & Arons Reference Hibschman and Arons2001; Arendt & Eilek Reference Arendt and Eilek2002). We choose a 1-D Jüttner distribution (Melrose & Gedalin Reference Melrose and Gedalin1999; Melrose et al. Reference Melrose, Gedalin, Kennett and Fletcher1999; Asseo & Riazuelo Reference Asseo and Riazuelo2000) and suggest that this should be the default choice, with a specific reason being required to justify any other choice. (In Part 2 a streaming distribution is modelled by Lorentz transforming a Jüttner distribution from its rest frame to the frame in which it is streaming.)
The combined distribution function, for electrons plus positrons, is then
where
![]() $u=\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FD}$
and
$u=\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FD}$
and
![]() $n$
is the number density. The parameter
$n$
is the number density. The parameter
![]() $\unicode[STIX]{x1D70C}=mc^{2}/T$
is the ratio of the rest energy of the electron to the temperature in energy units, with
$\unicode[STIX]{x1D70C}=mc^{2}/T$
is the ratio of the rest energy of the electron to the temperature in energy units, with
![]() $\unicode[STIX]{x1D70C}=1$
corresponding to
$\unicode[STIX]{x1D70C}=1$
corresponding to
![]() $T=0.511~\text{MeV}\approx 0.6\times 10^{10}\,K$
, and
$T=0.511~\text{MeV}\approx 0.6\times 10^{10}\,K$
, and
![]() $K_{1}(\unicode[STIX]{x1D70C})$
is the Macdonald function of order 1. One has
$K_{1}(\unicode[STIX]{x1D70C})$
is the Macdonald function of order 1. One has
![]() $\langle \unicode[STIX]{x1D6FE}\rangle \approx 1/\unicode[STIX]{x1D70C}$
for a highly relativistic distribution where
$\langle \unicode[STIX]{x1D6FE}\rangle \approx 1/\unicode[STIX]{x1D70C}$
for a highly relativistic distribution where
![]() $\unicode[STIX]{x1D70C}\ll 1$
.
$\unicode[STIX]{x1D70C}\ll 1$
.
3.2 RPDF for a Jüttner distribution
The integrand of (A 8) defining the RPDF
![]() $W(z)$
is singular at
$W(z)$
is singular at
![]() $\unicode[STIX]{x1D6FD}=z$
for
$\unicode[STIX]{x1D6FD}=z$
for
![]() $|z|<1$
. The singularity is treated following the Landau prescription:
$|z|<1$
. The singularity is treated following the Landau prescription:
![]() $\unicode[STIX]{x1D714}\rightarrow \unicode[STIX]{x1D714}+i0$
(we assume real
$\unicode[STIX]{x1D714}\rightarrow \unicode[STIX]{x1D714}+i0$
(we assume real
![]() $k_{\Vert }$
). With
$k_{\Vert }$
). With
![]() $z=\unicode[STIX]{x1D714}/k_{\Vert }c$
, this implies
$z=\unicode[STIX]{x1D714}/k_{\Vert }c$
, this implies
![]() $z\rightarrow z+i0$
for
$z\rightarrow z+i0$
for
![]() $k_{\Vert }>0$
and to
$k_{\Vert }>0$
and to
![]() $z\rightarrow z-i0$
for
$z\rightarrow z-i0$
for
![]() $k_{\Vert }<0$
. For
$k_{\Vert }<0$
. For
![]() $\unicode[STIX]{x1D714}>0$
, the resonant denominator is then replaced by
$\unicode[STIX]{x1D714}>0$
, the resonant denominator is then replaced by
![]() $i\unicode[STIX]{x03C0}\,\text{sgn}(k_{\Vert })\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D6FD}-z)$
where
$i\unicode[STIX]{x03C0}\,\text{sgn}(k_{\Vert })\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D6FD}-z)$
where
![]() $\text{sgn}(k_{\Vert })=k_{\Vert }/|k_{\Vert }|$
is the sign of
$\text{sgn}(k_{\Vert })=k_{\Vert }/|k_{\Vert }|$
is the sign of
![]() $k_{\Vert }$
. The RPDF may be expressed as
$k_{\Vert }$
. The RPDF may be expressed as
 $$\begin{eqnarray}\displaystyle W(z)=\left\{\begin{array}{@{}ll@{}}\left\langle {\displaystyle \frac{1}{\unicode[STIX]{x1D6FE}^{3}(\unicode[STIX]{x1D6FD}-z)^{2}}}\right\rangle ,\quad & \text{for}\,|z|>1,\\[12.0pt] \displaystyle {\displaystyle \frac{1}{n}}\left[\text{i}\unicode[STIX]{x03C0}\text{sgn}(k_{\Vert }){\displaystyle \frac{\text{d}g(u)}{\text{d}\unicode[STIX]{x1D6FD}}}|_{\unicode[STIX]{x1D6FD}=z}-2\unicode[STIX]{x1D6FE}^{2}g(u)|_{\unicode[STIX]{x1D6FD}=z}\right.\quad \\[12.0pt] \displaystyle \left.\quad -\,{\wp}\int _{-1}^{1}\,\text{d}\unicode[STIX]{x1D6FD}\,{\displaystyle \frac{g(u)|_{\unicode[STIX]{x1D6FD}=z}-g(u)}{(\unicode[STIX]{x1D6FD}-z)^{2}}}\right],\quad & \text{for}\,|z|\leqslant 1,\end{array}\right. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle W(z)=\left\{\begin{array}{@{}ll@{}}\left\langle {\displaystyle \frac{1}{\unicode[STIX]{x1D6FE}^{3}(\unicode[STIX]{x1D6FD}-z)^{2}}}\right\rangle ,\quad & \text{for}\,|z|>1,\\[12.0pt] \displaystyle {\displaystyle \frac{1}{n}}\left[\text{i}\unicode[STIX]{x03C0}\text{sgn}(k_{\Vert }){\displaystyle \frac{\text{d}g(u)}{\text{d}\unicode[STIX]{x1D6FD}}}|_{\unicode[STIX]{x1D6FD}=z}-2\unicode[STIX]{x1D6FE}^{2}g(u)|_{\unicode[STIX]{x1D6FD}=z}\right.\quad \\[12.0pt] \displaystyle \left.\quad -\,{\wp}\int _{-1}^{1}\,\text{d}\unicode[STIX]{x1D6FD}\,{\displaystyle \frac{g(u)|_{\unicode[STIX]{x1D6FD}=z}-g(u)}{(\unicode[STIX]{x1D6FD}-z)^{2}}}\right],\quad & \text{for}\,|z|\leqslant 1,\end{array}\right. & & \displaystyle\end{eqnarray}$$
where
![]() ${\wp}$
denotes a Cauchy principal value integral, and
${\wp}$
denotes a Cauchy principal value integral, and
![]() $u=\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FD}=\unicode[STIX]{x1D6FD}/(1-\unicode[STIX]{x1D6FD}^{2})^{1/2}$
. The expression for
$u=\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FD}=\unicode[STIX]{x1D6FD}/(1-\unicode[STIX]{x1D6FD}^{2})^{1/2}$
. The expression for
![]() $|z|>1$
follows from a partial integration of (A 8) and that for
$|z|>1$
follows from a partial integration of (A 8) and that for
![]() $|z|\leqslant 1$
is derived in appendix B. Note that the expression for
$|z|\leqslant 1$
is derived in appendix B. Note that the expression for
![]() $|z|>1$
can be misleading if applied to
$|z|>1$
can be misleading if applied to
![]() $|z|<1$
. Specifically, the form for
$|z|<1$
. Specifically, the form for
![]() $|z|>1$
is real and positive definite, whereas for
$|z|>1$
is real and positive definite, whereas for
![]() $|z|<1$
the RPDF is complex and its real part is negative for
$|z|<1$
the RPDF is complex and its real part is negative for
![]() $0<|z|\leqslant z_{0}$
, where
$0<|z|\leqslant z_{0}$
, where
![]() $z_{0}$
is identified below. For a Jüttner distribution the imaginary part of
$z_{0}$
is identified below. For a Jüttner distribution the imaginary part of
![]() $W(z)$
follows from (3.2) with (3.1) implying
$W(z)$
follows from (3.2) with (3.1) implying
The RPDF
![]() $W(z)$
for the distribution (3.1) can be expressed in terms of another RPDF,
$W(z)$
for the distribution (3.1) can be expressed in terms of another RPDF,
The properties of the RPDF
![]() $T(z,\unicode[STIX]{x1D70C})$
were summarized by Godfrey, Newberger & Taggart (Reference Godfrey, Newberger and Taggart1975), cf. also Melrose (Reference Melrose2008). We note two alternative forms for
$T(z,\unicode[STIX]{x1D70C})$
were summarized by Godfrey, Newberger & Taggart (Reference Godfrey, Newberger and Taggart1975), cf. also Melrose (Reference Melrose2008). We note two alternative forms for
![]() $T(z,\unicode[STIX]{x1D70C})$
given by Godfrey et al. (Reference Godfrey, Newberger and Taggart1975),
$T(z,\unicode[STIX]{x1D70C})$
given by Godfrey et al. (Reference Godfrey, Newberger and Taggart1975),
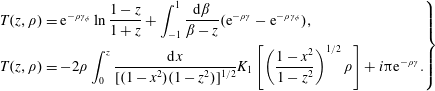 $$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}l@{}}T(z,\unicode[STIX]{x1D70C})=\text{e}^{-\unicode[STIX]{x1D70C}\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D719}}}\ln {\displaystyle \frac{1-z}{1+z}}+\displaystyle \int _{-1}^{1}{\displaystyle \frac{\text{d}\unicode[STIX]{x1D6FD}}{\unicode[STIX]{x1D6FD}-z}}(\text{e}^{-\unicode[STIX]{x1D70C}\unicode[STIX]{x1D6FE}}-\text{e}^{-\unicode[STIX]{x1D70C}\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D719}}}),\\[11.0pt] \displaystyle T(z,\unicode[STIX]{x1D70C})=-2\unicode[STIX]{x1D70C}\int _{0}^{z}{\displaystyle \frac{\text{d}x}{[(1-x^{2})(1-z^{2})]^{1/2}}}K_{1}\left[\left({\displaystyle \frac{1-x^{2}}{1-z^{2}}}\right)^{1/2}\unicode[STIX]{x1D70C}\right]+i\unicode[STIX]{x03C0}\text{e}^{-\unicode[STIX]{x1D70C}\unicode[STIX]{x1D6FE}}.\end{array}\right\} & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}l@{}}T(z,\unicode[STIX]{x1D70C})=\text{e}^{-\unicode[STIX]{x1D70C}\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D719}}}\ln {\displaystyle \frac{1-z}{1+z}}+\displaystyle \int _{-1}^{1}{\displaystyle \frac{\text{d}\unicode[STIX]{x1D6FD}}{\unicode[STIX]{x1D6FD}-z}}(\text{e}^{-\unicode[STIX]{x1D70C}\unicode[STIX]{x1D6FE}}-\text{e}^{-\unicode[STIX]{x1D70C}\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D719}}}),\\[11.0pt] \displaystyle T(z,\unicode[STIX]{x1D70C})=-2\unicode[STIX]{x1D70C}\int _{0}^{z}{\displaystyle \frac{\text{d}x}{[(1-x^{2})(1-z^{2})]^{1/2}}}K_{1}\left[\left({\displaystyle \frac{1-x^{2}}{1-z^{2}}}\right)^{1/2}\unicode[STIX]{x1D70C}\right]+i\unicode[STIX]{x03C0}\text{e}^{-\unicode[STIX]{x1D70C}\unicode[STIX]{x1D6FE}}.\end{array}\right\} & & \displaystyle\end{eqnarray}$$
In our detailed calculations we compared all three forms, and confirmed their equivalence.
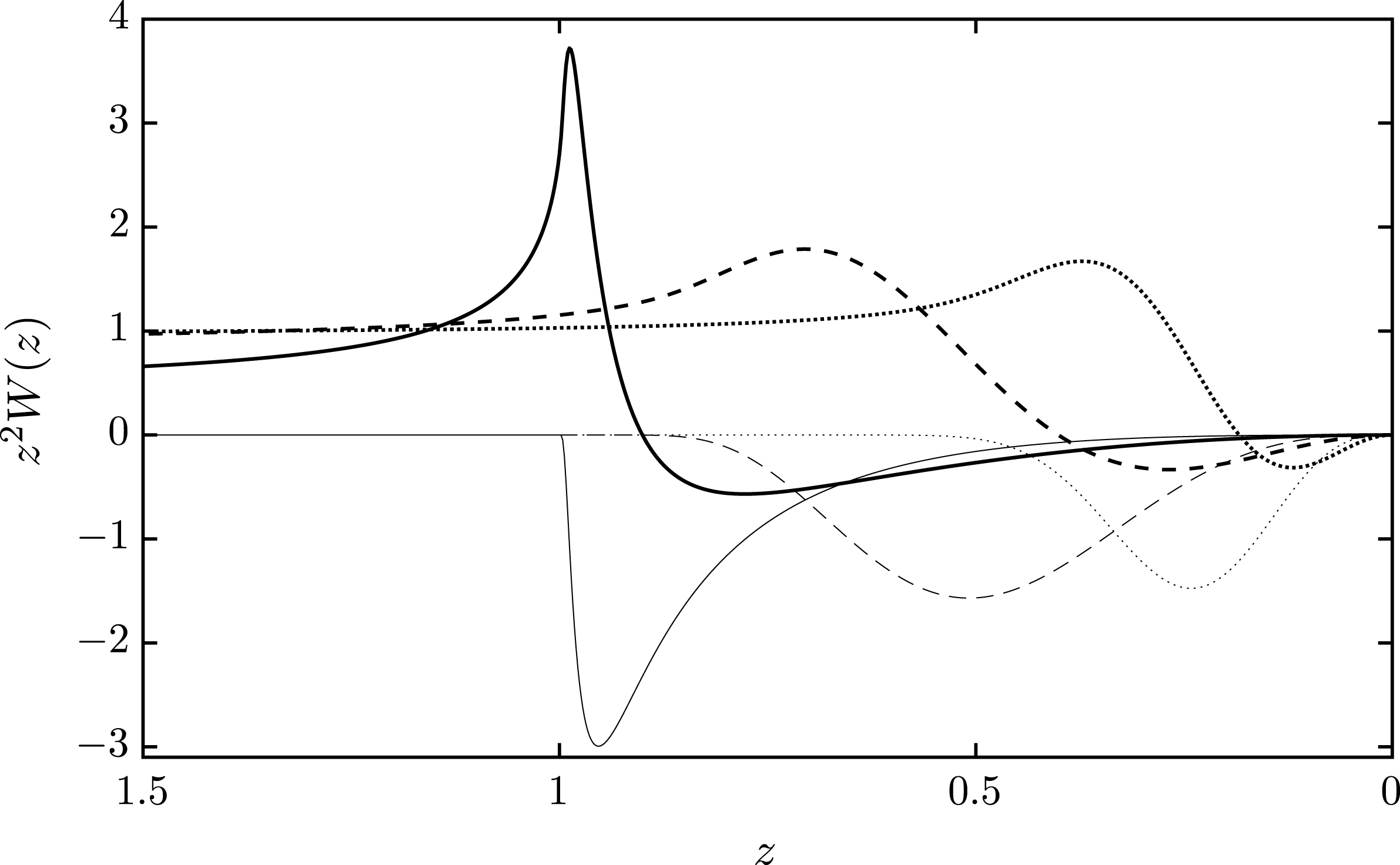
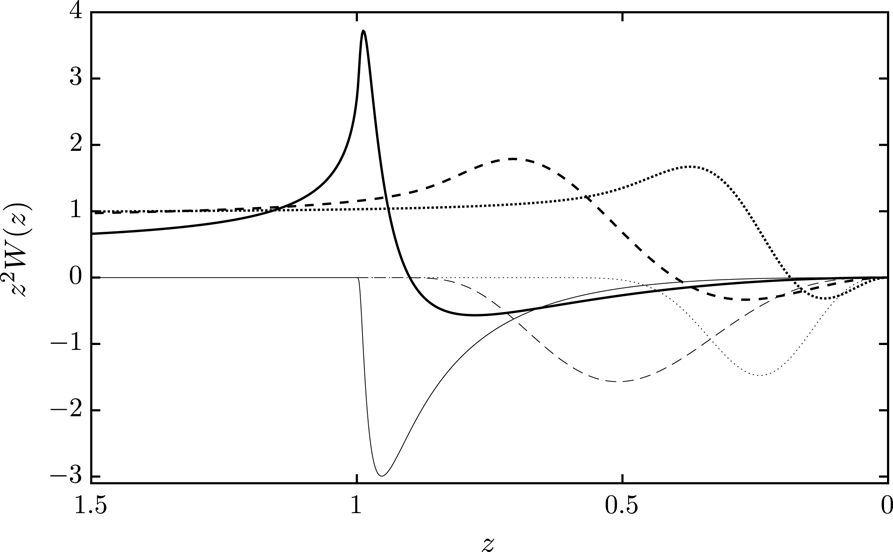
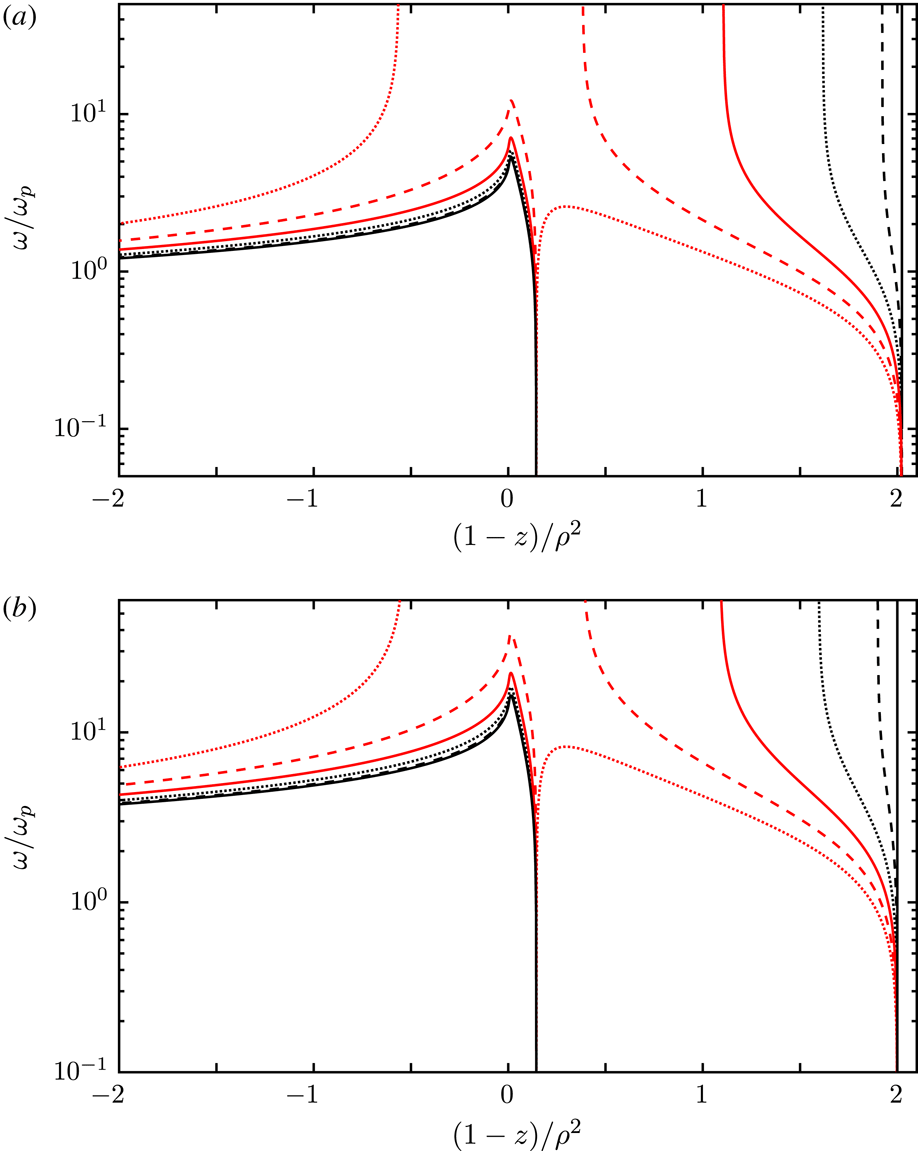
Figure 1. The RPDF
![]() $z^{2}W(z)$
is plotted as a function of
$z^{2}W(z)$
is plotted as a function of
![]() $z$
for 1-D Jüttner distributions. The thick curves correspond to the real part and the thin curves to the imaginary part of
$z$
for 1-D Jüttner distributions. The thick curves correspond to the real part and the thin curves to the imaginary part of
![]() $z^{2}W(z)$
for
$z^{2}W(z)$
for
![]() $\unicode[STIX]{x1D70C}=50$
(dotted),
$\unicode[STIX]{x1D70C}=50$
(dotted),
![]() $\unicode[STIX]{x1D70C}=10$
(dashed) and
$\unicode[STIX]{x1D70C}=10$
(dashed) and
![]() $\unicode[STIX]{x1D70C}=1$
(solid). The imaginary parts are identically zero for
$\unicode[STIX]{x1D70C}=1$
(solid). The imaginary parts are identically zero for
![]() $z\geqslant 1$
and negative for
$z\geqslant 1$
and negative for
![]() $z<1$
. Note that
$z<1$
. Note that
![]() $z$
increases from right to left to facilitate comparison with dispersion curves shown below.
$z$
increases from right to left to facilitate comparison with dispersion curves shown below.
Examples of
![]() $z^{2}W(z)$
for the distribution (3.1) are shown in figure 1 for three temperatures, ranging from a non-relativistic value,
$z^{2}W(z)$
for the distribution (3.1) are shown in figure 1 for three temperatures, ranging from a non-relativistic value,
![]() $\unicode[STIX]{x1D70C}=50\gg 1$
(dotted), to a value,
$\unicode[STIX]{x1D70C}=50\gg 1$
(dotted), to a value,
![]() $\unicode[STIX]{x1D70C}=1$
(solid), where relativistic effects are significant. A similar plot was presented by Melrose & Gedalin (Reference Melrose and Gedalin1999), and we make two notable changes in figure 1; we include the imaginary parts, shown by the thin curves, and we plot the curves such that the superluminal regime,
$\unicode[STIX]{x1D70C}=1$
(solid), where relativistic effects are significant. A similar plot was presented by Melrose & Gedalin (Reference Melrose and Gedalin1999), and we make two notable changes in figure 1; we include the imaginary parts, shown by the thin curves, and we plot the curves such that the superluminal regime,
![]() $z>1$
is to the left of
$z>1$
is to the left of
![]() $z=1$
and the subluminal regime is to the right of
$z=1$
and the subluminal regime is to the right of
![]() $z=1$
. The peak in the RPDF evident in figure 1 becomes higher, narrower and closer to
$z=1$
. The peak in the RPDF evident in figure 1 becomes higher, narrower and closer to
![]() $z=1$
with decreasing
$z=1$
with decreasing
![]() $\unicode[STIX]{x1D70C}$
. We show this peak on a fine scale and on a very fine scale in figure 2 for
$\unicode[STIX]{x1D70C}$
. We show this peak on a fine scale and on a very fine scale in figure 2 for
![]() $\unicode[STIX]{x1D70C}=0.1$
(dashed) and
$\unicode[STIX]{x1D70C}=0.1$
(dashed) and
![]() $\unicode[STIX]{x1D70C}=0.01$
(solid). Note that the shape of the peak near
$\unicode[STIX]{x1D70C}=0.01$
(solid). Note that the shape of the peak near
![]() $z=1$
scales in a characteristic way with
$z=1$
scales in a characteristic way with
![]() $\unicode[STIX]{x1D70C}$
. Numerical estimates based on the scaling apparent in these figures are given below.
$\unicode[STIX]{x1D70C}$
. Numerical estimates based on the scaling apparent in these figures are given below.
For numerical results and plots we use, unless stated otherwise, pulsar period
![]() $P=1~\text{s}$
, period derivative
$P=1~\text{s}$
, period derivative
![]() ${\dot{P}}=10^{-15}$
, emission height at radius
${\dot{P}}=10^{-15}$
, emission height at radius
![]() $r/r_{\text{L}}=0.1$
, where
$r/r_{\text{L}}=0.1$
, where
![]() $r_{\text{L}}=Pc/2\unicode[STIX]{x03C0}$
is the light-cylinder radius, and multiplicity
$r_{\text{L}}=Pc/2\unicode[STIX]{x03C0}$
is the light-cylinder radius, and multiplicity
![]() $\unicode[STIX]{x1D705}=10^{5}$
. For these parameter values
$\unicode[STIX]{x1D705}=10^{5}$
. For these parameter values
![]() $\unicode[STIX]{x1D6FD}_{\text{A}}\approx 5.0\times 10^{3}$
&
$\unicode[STIX]{x1D6FD}_{\text{A}}\approx 5.0\times 10^{3}$
&
![]() $\unicode[STIX]{x1D6FE}_{\text{A}}\approx 3.6\times 10^{3}$
for
$\unicode[STIX]{x1D6FE}_{\text{A}}\approx 3.6\times 10^{3}$
for
![]() $\unicode[STIX]{x1D70C}=0.1$
, and
$\unicode[STIX]{x1D70C}=0.1$
, and
![]() $\unicode[STIX]{x1D6FD}_{\text{A}}\approx 1.6\times 10^{3}$
&
$\unicode[STIX]{x1D6FD}_{\text{A}}\approx 1.6\times 10^{3}$
&
![]() $\unicode[STIX]{x1D6FE}_{\text{A}}\approx 1.1\times 10^{3}$
for
$\unicode[STIX]{x1D6FE}_{\text{A}}\approx 1.1\times 10^{3}$
for
![]() $\unicode[STIX]{x1D70C}=0.01$
, where
$\unicode[STIX]{x1D70C}=0.01$
, where
![]() $\unicode[STIX]{x1D6FE}_{\text{A}}$
is given by (A 12). In some calculations we vary
$\unicode[STIX]{x1D6FE}_{\text{A}}$
is given by (A 12). In some calculations we vary
![]() $\unicode[STIX]{x1D6FD}_{\text{A}}$
which can be achieved by varying a number of pulsar parameters as
$\unicode[STIX]{x1D6FD}_{\text{A}}$
which can be achieved by varying a number of pulsar parameters as
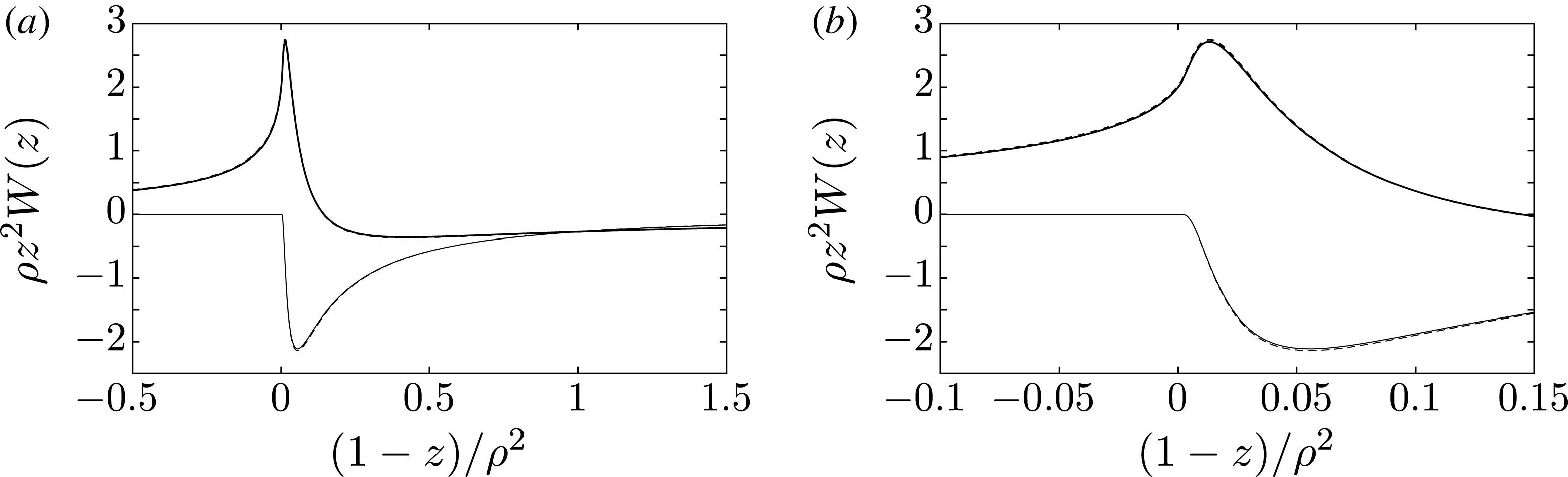
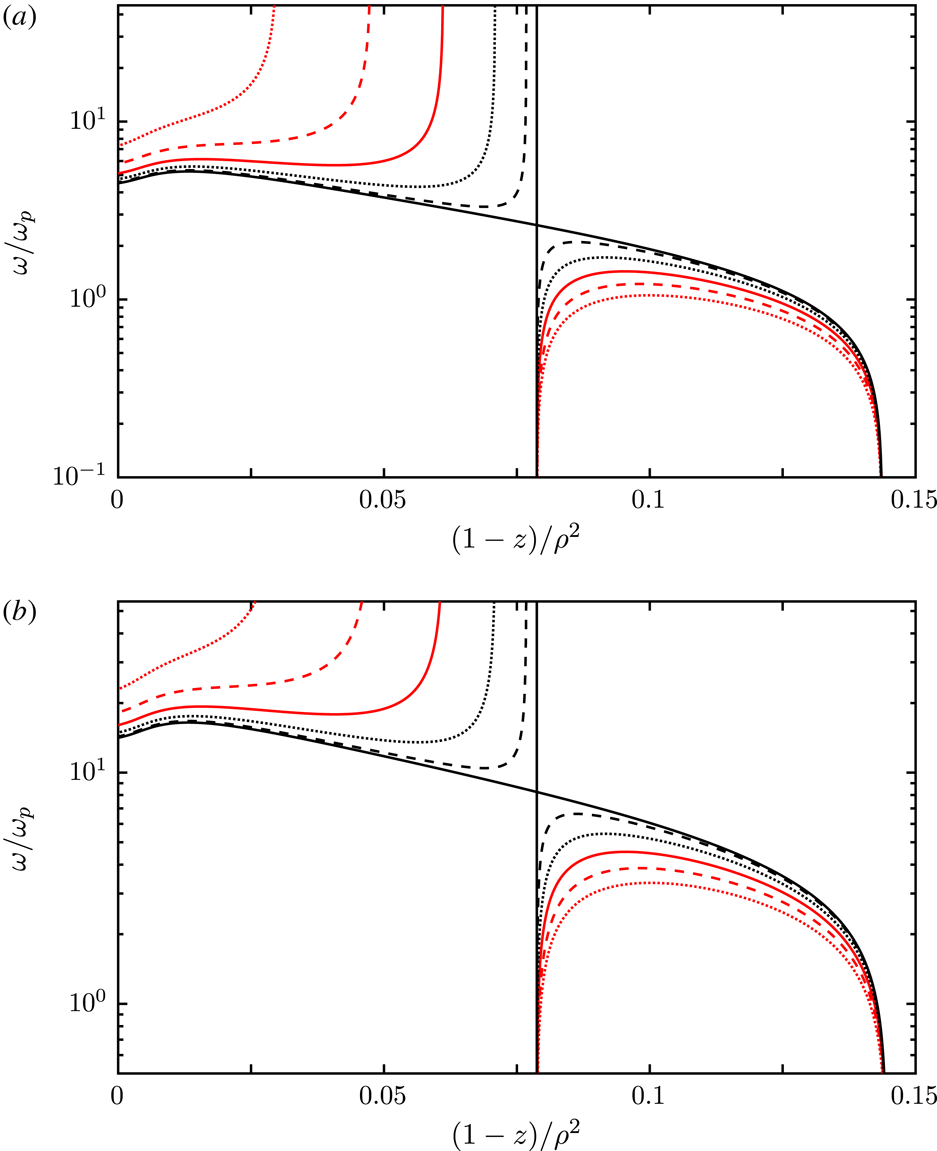
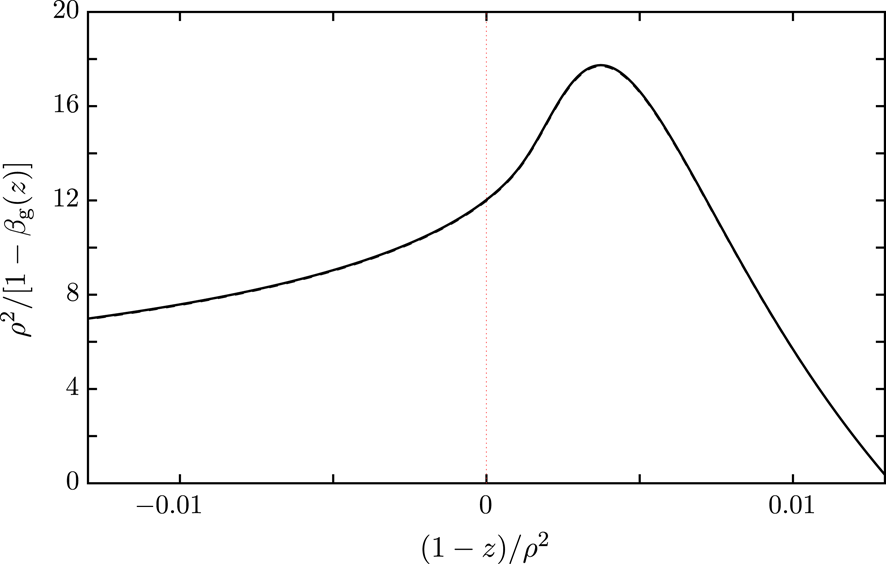
Figure 2. As for figure 1 but with
![]() $\unicode[STIX]{x1D70C}z^{2}W(z)$
plotted against
$\unicode[STIX]{x1D70C}z^{2}W(z)$
plotted against
![]() $(1-z)/\unicode[STIX]{x1D70C}^{2}$
for
$(1-z)/\unicode[STIX]{x1D70C}^{2}$
for
![]() $\unicode[STIX]{x1D70C}=0.1$
(dashed) and
$\unicode[STIX]{x1D70C}=0.1$
(dashed) and
![]() $\unicode[STIX]{x1D70C}=0.01$
(solid) around
$\unicode[STIX]{x1D70C}=0.01$
(solid) around
![]() $z=1$
on a fine scale (a) and on a very fine scale (b). With these scalings of the vertical and horizontal axes, the plots for
$z=1$
on a fine scale (a) and on a very fine scale (b). With these scalings of the vertical and horizontal axes, the plots for
![]() $\unicode[STIX]{x1D70C}=0.1$
and
$\unicode[STIX]{x1D70C}=0.1$
and
![]() $\unicode[STIX]{x1D70C}=0.01$
are nearly indistinguishable.
$\unicode[STIX]{x1D70C}=0.01$
are nearly indistinguishable.
3.3 Properties of the RPDF
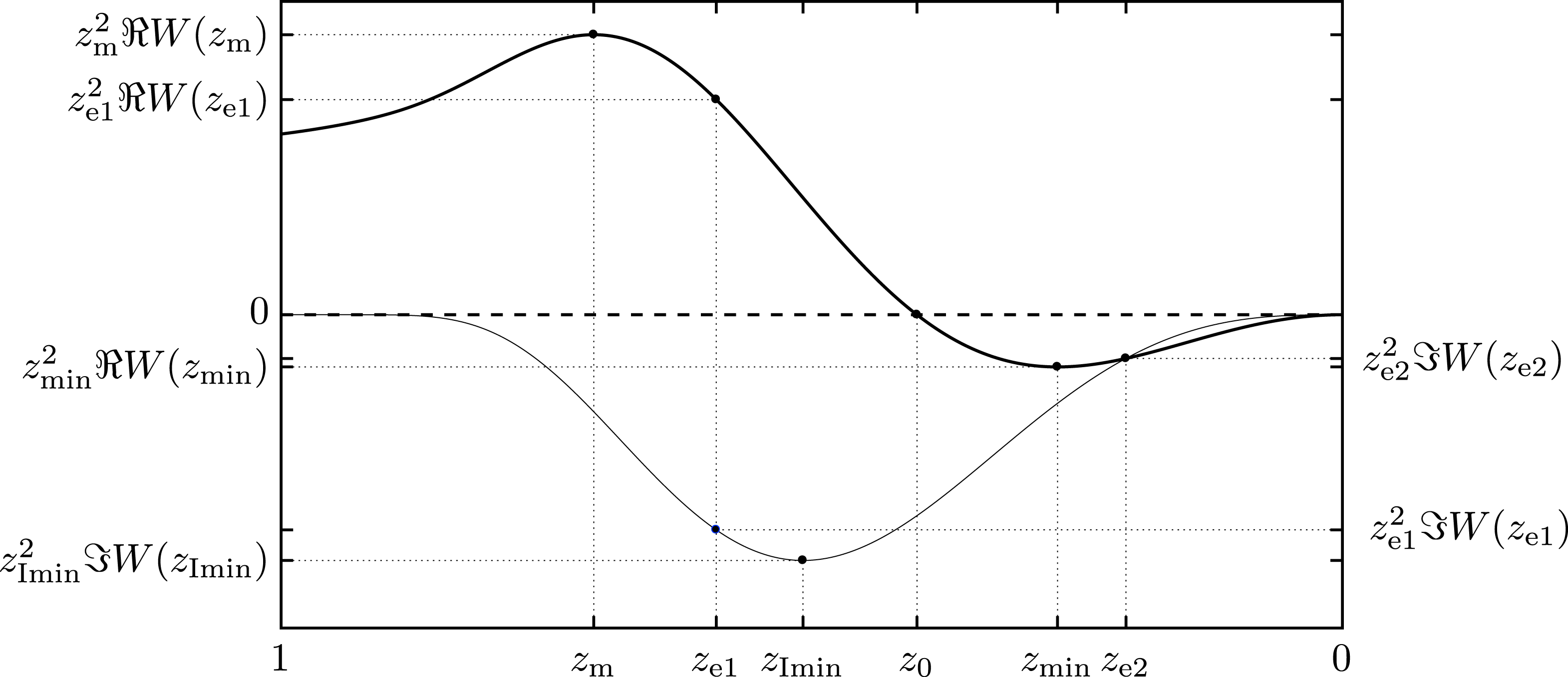
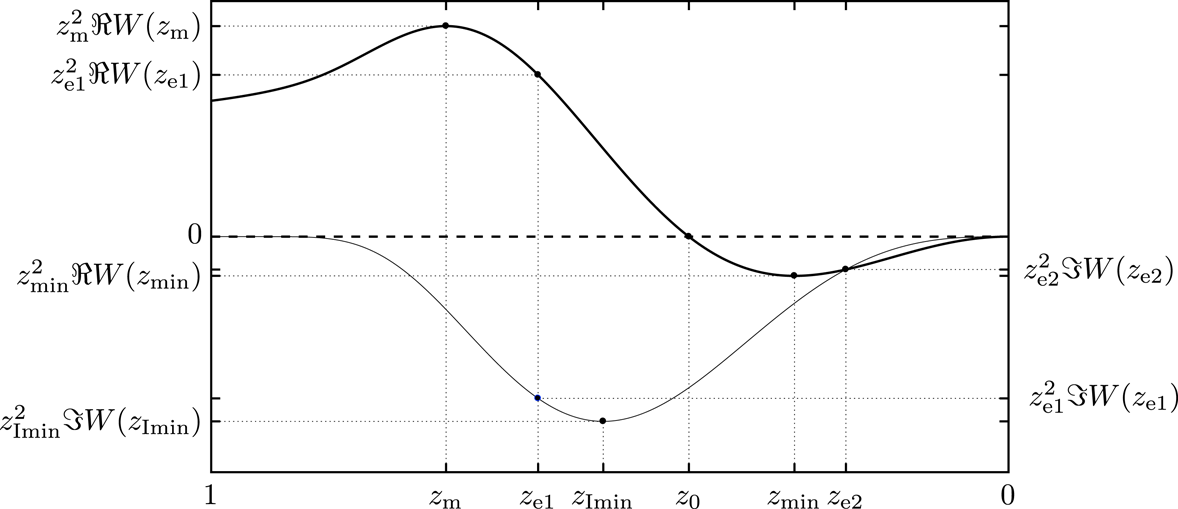
Figure 3. A plot of
![]() $z^{2}\text{Re}W(z)$
(thick solid) and
$z^{2}\text{Re}W(z)$
(thick solid) and
![]() $z^{2}\text{Im}W(z)$
(thin solid) over
$z^{2}\text{Im}W(z)$
(thin solid) over
![]() $1>z>0$
illustrating specific values of
$1>z>0$
illustrating specific values of
![]() $z$
:
$z$
:
![]() $z_{\text{m}}$
where
$z_{\text{m}}$
where
![]() $z^{2}\text{Re}W(z)$
is a maximum,
$z^{2}\text{Re}W(z)$
is a maximum,
![]() $z_{0}$
where
$z_{0}$
where
![]() $z^{2}\text{Re}W(z)$
passes through zero,
$z^{2}\text{Re}W(z)$
passes through zero,
![]() $z_{\text{min}}$
where
$z_{\text{min}}$
where
![]() $z^{2}\text{Re}W(z)$
is a minimum,
$z^{2}\text{Re}W(z)$
is a minimum,
![]() $z_{\text{Imin}}$
where
$z_{\text{Imin}}$
where
![]() $z^{2}\text{Im}W(z)$
is a minimum, and
$z^{2}\text{Im}W(z)$
is a minimum, and
![]() $z_{\text{e1,2}}$
where
$z_{\text{e1,2}}$
where
![]() $|z^{2}\text{Re}W(z)|=|z^{2}\text{Im}W(z)|$
.
$|z^{2}\text{Re}W(z)|=|z^{2}\text{Im}W(z)|$
.
In figure 3 we present a typical plot of the real (thick solid) and imaginary (thin solid) part of the RPDF
![]() $z^{2}W(z)$
over
$z^{2}W(z)$
over
![]() $1>z>0$
. We denote the critical
$1>z>0$
. We denote the critical
![]() $z$
values and the corresponding value of the real and imaginary parts of
$z$
values and the corresponding value of the real and imaginary parts of
![]() $z^{2}W(z)$
at these
$z^{2}W(z)$
at these
![]() $z$
values. These critical values of
$z$
values. These critical values of
![]() $z$
are
$z$
are
![]() $z_{\text{m}}$
where
$z_{\text{m}}$
where
![]() $z^{2}\text{Re}W(z)$
is a maximum,
$z^{2}\text{Re}W(z)$
is a maximum,
![]() $z_{0}$
where
$z_{0}$
where
![]() $z^{2}\text{Re}W(z)$
passes through zero,
$z^{2}\text{Re}W(z)$
passes through zero,
![]() $z_{\text{min}}$
where
$z_{\text{min}}$
where
![]() $z^{2}\text{Re}W(z)$
is a minimum,
$z^{2}\text{Re}W(z)$
is a minimum,
![]() $z_{\text{Imin}}$
where
$z_{\text{Imin}}$
where
![]() $z^{2}\text{Im}W(z)$
is a minimum and
$z^{2}\text{Im}W(z)$
is a minimum and
![]() $z_{\text{e}1,2}$
where
$z_{\text{e}1,2}$
where
![]() $|z^{2}\text{Re}W(z)|=|z^{2}\text{Im}W(z)|$
. We note that
$|z^{2}\text{Re}W(z)|=|z^{2}\text{Im}W(z)|$
. We note that
In the rest frame of the plasma these critical points only depend on the value of
![]() $\unicode[STIX]{x1D70C}$
. For
$\unicode[STIX]{x1D70C}$
. For
![]() $\unicode[STIX]{x1D70C}\ll 1$
, the critical
$\unicode[STIX]{x1D70C}\ll 1$
, the critical
![]() $z$
values vary as
$z$
values vary as
![]() $z\approx 1-\unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D70C}^{2}$
and the corresponding Lorentz factors as
$z\approx 1-\unicode[STIX]{x1D6FC}_{1}\unicode[STIX]{x1D70C}^{2}$
and the corresponding Lorentz factors as
![]() $\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D719}}\approx \unicode[STIX]{x1D6FC}_{2}/\unicode[STIX]{x1D70C}$
, and the real and imaginary components of
$\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D719}}\approx \unicode[STIX]{x1D6FC}_{2}/\unicode[STIX]{x1D70C}$
, and the real and imaginary components of
![]() $z^{2}W(z)$
vary as
$z^{2}W(z)$
vary as
![]() ${\approx}\unicode[STIX]{x1D6FC}_{3}/\unicode[STIX]{x1D70C}$
. We give approximate values of
${\approx}\unicode[STIX]{x1D6FC}_{3}/\unicode[STIX]{x1D70C}$
. We give approximate values of
![]() $\unicode[STIX]{x1D6FC}_{i}$
in table 1 for both
$\unicode[STIX]{x1D6FC}_{i}$
in table 1 for both
![]() $\unicode[STIX]{x1D70C}\ll 1$
and
$\unicode[STIX]{x1D70C}\ll 1$
and
![]() $\unicode[STIX]{x1D70C}=1$
. We plot these critical points in figure 4 where
$\unicode[STIX]{x1D70C}=1$
. We plot these critical points in figure 4 where
![]() $\unicode[STIX]{x1D70C}$
varies between
$\unicode[STIX]{x1D70C}$
varies between
![]() $10^{-2}$
and 50.
$10^{-2}$
and 50.
Table 1. Empirical values for parameters
![]() $\unicode[STIX]{x1D6FC}_{i}$
for
$\unicode[STIX]{x1D6FC}_{i}$
for
![]() $i=1,2,3$
.
$i=1,2,3$
.
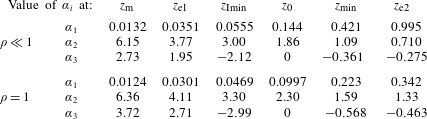

Figure 4. (a) Plots of
![]() $\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D719}}$
against
$\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D719}}$
against
![]() $\unicode[STIX]{x1D70C}$
with
$\unicode[STIX]{x1D70C}$
with
![]() $\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D719}}$
evaluated at
$\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D719}}$
evaluated at
![]() $z=z_{\text{m}}$
(thick solid), at
$z=z_{\text{m}}$
(thick solid), at
![]() $z=z_{0}$
(dashed), at
$z=z_{0}$
(dashed), at
![]() $z=z_{\text{min}}$
(thin solid), at
$z=z_{\text{min}}$
(thin solid), at
![]() $z=z_{\text{Imin}}$
(dotted), at
$z=z_{\text{Imin}}$
(dotted), at
![]() $z=z_{\text{e}1}$
(thick dash-dotted) and at
$z=z_{\text{e}1}$
(thick dash-dotted) and at
![]() $z=z_{\text{e}2}$
(thin dash-dotted). (b) Magnitude of
$z=z_{\text{e}2}$
(thin dash-dotted). (b) Magnitude of
![]() $\text{Re}z^{2}W(z)$
at
$\text{Re}z^{2}W(z)$
at
![]() $z=z_{\text{m}}$
(thick solid), at
$z=z_{\text{m}}$
(thick solid), at
![]() $z=z_{\text{min}}$
(thin solid), at
$z=z_{\text{min}}$
(thin solid), at
![]() $z_{\text{e}1}$
(thick dash-dotted) and
$z_{\text{e}1}$
(thick dash-dotted) and
![]() $z_{\text{e}2}$
(thin dash-dotted) where
$z_{\text{e}2}$
(thin dash-dotted) where
![]() $|\text{Im}z^{2}W(z)|=|\text{Re}z^{2}W(z)|$
, and at
$|\text{Im}z^{2}W(z)|=|\text{Re}z^{2}W(z)|$
, and at
![]() $z=z_{\text{Imin}}$
where
$z=z_{\text{Imin}}$
where
![]() $|\text{Im}z^{2}W(z)|$
(dotted).
$|\text{Im}z^{2}W(z)|$
(dotted).
The average value of powers of
![]() $\unicode[STIX]{x1D6FE}$
over a Jüttner distribution are related to
$\unicode[STIX]{x1D6FE}$
over a Jüttner distribution are related to
![]() $\unicode[STIX]{x1D70C}$
as shown in table 2 (Melrose & Gedalin Reference Melrose and Gedalin1999). The approximations given for
$\unicode[STIX]{x1D70C}$
as shown in table 2 (Melrose & Gedalin Reference Melrose and Gedalin1999). The approximations given for
![]() $\unicode[STIX]{x1D70C}\ll 1$
are particularly important and simple.
$\unicode[STIX]{x1D70C}\ll 1$
are particularly important and simple.
Table 2. Averages over a Jüttner distribution as given by Melrose & Gedalin (Reference Melrose and Gedalin1999). The functions
![]() $K_{i}(\unicode[STIX]{x1D70C})$
are modified Bessel functions of second type, and
$K_{i}(\unicode[STIX]{x1D70C})$
are modified Bessel functions of second type, and
![]() $Ki_{n}(\unicode[STIX]{x1D70C})$
are Bickley functions defined as the
$Ki_{n}(\unicode[STIX]{x1D70C})$
are Bickley functions defined as the
![]() $n^{\text{th}}$
integral of
$n^{\text{th}}$
integral of
![]() $K_{0}(\unicode[STIX]{x1D70C})$
.
$K_{0}(\unicode[STIX]{x1D70C})$
.

4 Wave dispersion for
 $\unicode[STIX]{x1D70C}\geqslant 1$
$\unicode[STIX]{x1D70C}\geqslant 1$
In this section, before considering wave dispersion in a pulsar plasma with
![]() $\unicode[STIX]{x1D70C}\ll 1$
, for comparison we discuss non-relativistic counterparts: the cold-plasma limit,
$\unicode[STIX]{x1D70C}\ll 1$
, for comparison we discuss non-relativistic counterparts: the cold-plasma limit,
![]() $\unicode[STIX]{x1D70C}\rightarrow \infty$
and a non-relativistic thermal case
$\unicode[STIX]{x1D70C}\rightarrow \infty$
and a non-relativistic thermal case
![]() $\unicode[STIX]{x1D70C}\gg 1$
. We then discuss the case
$\unicode[STIX]{x1D70C}\gg 1$
. We then discuss the case
![]() $\unicode[STIX]{x1D70C}=1$
. The highly relativistic regime,
$\unicode[STIX]{x1D70C}=1$
. The highly relativistic regime,
![]() $\unicode[STIX]{x1D70C}\ll 1$
, is discussed in the next section.
$\unicode[STIX]{x1D70C}\ll 1$
, is discussed in the next section.
4.1 Cold-plasma limit
The cold-plasma limit corresponds to
The non-zero terms of
![]() $\unicode[STIX]{x1D6EC}_{ij}$
are then given by (A 11) with
$\unicode[STIX]{x1D6EC}_{ij}$
are then given by (A 11) with
![]() $a=1+1/\unicode[STIX]{x1D6FD}_{\text{A}}^{2}$
,
$a=1+1/\unicode[STIX]{x1D6FD}_{\text{A}}^{2}$
,
![]() $b=1$
and
$b=1$
and
![]() $z^{2}W(z)=1$
. This limit may also be treated using the cold-plasma model, with the ions replaced by positrons. In cold-plasma theory, it is conventional to solve the dispersion equation for the square of the refractive index,
$z^{2}W(z)=1$
. This limit may also be treated using the cold-plasma model, with the ions replaced by positrons. In cold-plasma theory, it is conventional to solve the dispersion equation for the square of the refractive index,
![]() $N^{2}=k^{2}c^{2}/\unicode[STIX]{x1D714}^{2}=1/z^{2}\cos ^{2}\unicode[STIX]{x1D703}$
, as a function of
$N^{2}=k^{2}c^{2}/\unicode[STIX]{x1D714}^{2}=1/z^{2}\cos ^{2}\unicode[STIX]{x1D703}$
, as a function of
![]() $\unicode[STIX]{x1D714}$
and the angle
$\unicode[STIX]{x1D714}$
and the angle
![]() $\unicode[STIX]{x1D703}$
of wave propagation (Stix Reference Stix1962).
$\unicode[STIX]{x1D703}$
of wave propagation (Stix Reference Stix1962).
4.1.1 The X mode
The dispersion equation for the X-mode in the cold-plasma limit follows from (2.4) using (4.1) as
The X mode may be interpreted as a magnetoacoustic wave with
![]() $z_{\text{A}}c$
the magnetohydrodynamic (MHD) speed when the displacement current is included. The polarization vector for the X mode is along the 2-axis, that is, along the direction
$z_{\text{A}}c$
the magnetohydrodynamic (MHD) speed when the displacement current is included. The polarization vector for the X mode is along the 2-axis, that is, along the direction
![]() $\boldsymbol{k}\times \boldsymbol{B}$
.
$\boldsymbol{k}\times \boldsymbol{B}$
.
4.1.2 Parallel A and L modes
With the cold-plasma assumption (4.1) one obtains from (2.3) the expression for A mode in a cold plasma as
From (4.2) and (4.3) it is evident that the dispersion relations for the X and A modes are the same for parallel propagation. The polarization of the A mode is along the
![]() $1$
-axis.
$1$
-axis.
The expression for the L mode in a cold plasma is obtained from (2.3) using (4.1) as
The polarization is longitudinal, which is along
![]() $\boldsymbol{B}$
for parallel propagation.
$\boldsymbol{B}$
for parallel propagation.
4.1.3 Alfvén and O modes
The Alfvén and O modes (2.5) using the cold-plasma limit (4.1) reduce to
For
![]() $\unicode[STIX]{x1D6FD}_{\text{A}}^{2}\gg 1$
we have
$\unicode[STIX]{x1D6FD}_{\text{A}}^{2}\gg 1$
we have
![]() $z_{\text{A}}^{2}\approx 1$
which allows us to write (4.5) as
$z_{\text{A}}^{2}\approx 1$
which allows us to write (4.5) as
where the final approximation applies for
![]() $\unicode[STIX]{x1D714}^{2}\gg \unicode[STIX]{x1D714}_{\text{p}}^{2}$
. Equation (4.6) implies propagating waves for
$\unicode[STIX]{x1D714}^{2}\gg \unicode[STIX]{x1D714}_{\text{p}}^{2}$
. Equation (4.6) implies propagating waves for
![]() $\unicode[STIX]{x1D714}^{2}>\unicode[STIX]{x1D714}_{\text{p}}^{2}$
and for
$\unicode[STIX]{x1D714}^{2}>\unicode[STIX]{x1D714}_{\text{p}}^{2}$
and for
![]() $\unicode[STIX]{x1D714}^{2}<\unicode[STIX]{x1D714}_{\text{p}}^{2}\cos ^{2}\unicode[STIX]{x1D703}$
, with a stop band (evanescent waves) in the range
$\unicode[STIX]{x1D714}^{2}<\unicode[STIX]{x1D714}_{\text{p}}^{2}\cos ^{2}\unicode[STIX]{x1D703}$
, with a stop band (evanescent waves) in the range
![]() $\unicode[STIX]{x1D714}_{\text{p}}^{2}\cos ^{2}\unicode[STIX]{x1D703}<\unicode[STIX]{x1D714}^{2}<\unicode[STIX]{x1D714}_{\text{p}}^{2}$
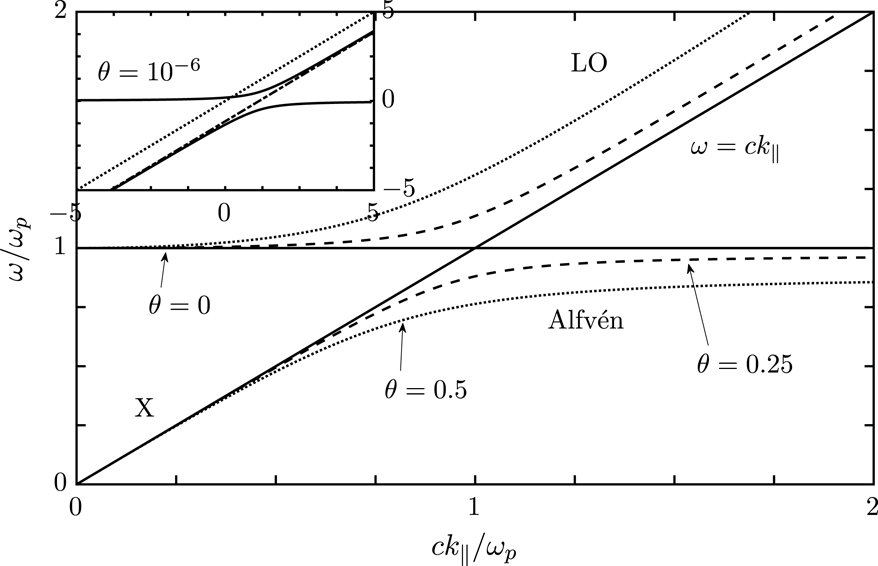
. The higher-frequency branch corresponds to the O mode and the lower-frequency branch to the Alfvén mode. For this cold-plasma case the reconnection of the L and A modes to form these two oblique modes is illustrated in figure 5, which is similar to a figure presented by Lyutikov (Reference Lyutikov1999).
$\unicode[STIX]{x1D714}_{\text{p}}^{2}\cos ^{2}\unicode[STIX]{x1D703}<\unicode[STIX]{x1D714}^{2}<\unicode[STIX]{x1D714}_{\text{p}}^{2}$
. The higher-frequency branch corresponds to the O mode and the lower-frequency branch to the Alfvén mode. For this cold-plasma case the reconnection of the L and A modes to form these two oblique modes is illustrated in figure 5, which is similar to a figure presented by Lyutikov (Reference Lyutikov1999).
In a relativistic plasma, an approximation to (2.5) that is similar to (4.6) may be obtained by regarding
![]() $\unicode[STIX]{x1D714}_{\text{L}}^{2}(z)$
as a constant (over a small range of
$\unicode[STIX]{x1D714}_{\text{L}}^{2}(z)$
as a constant (over a small range of
![]() $z$
values) and assuming
$z$
values) and assuming
![]() $b\approx 1$
,
$b\approx 1$
,
![]() $z_{\text{A}}^{2}\approx 1$
. The dispersion relation reduces to
$z_{\text{A}}^{2}\approx 1$
. The dispersion relation reduces to
Analogous to the cold-plasma case, as
![]() $\unicode[STIX]{x1D703}$
increases the reconnected modes move apart, the O mode to higher
$\unicode[STIX]{x1D703}$
increases the reconnected modes move apart, the O mode to higher
![]() $\unicode[STIX]{x1D714}$
and larger
$\unicode[STIX]{x1D714}$
and larger
![]() $z$
, and the Alfvén mode to lower
$z$
, and the Alfvén mode to lower
![]() $\unicode[STIX]{x1D714}$
.
$\unicode[STIX]{x1D714}$
.
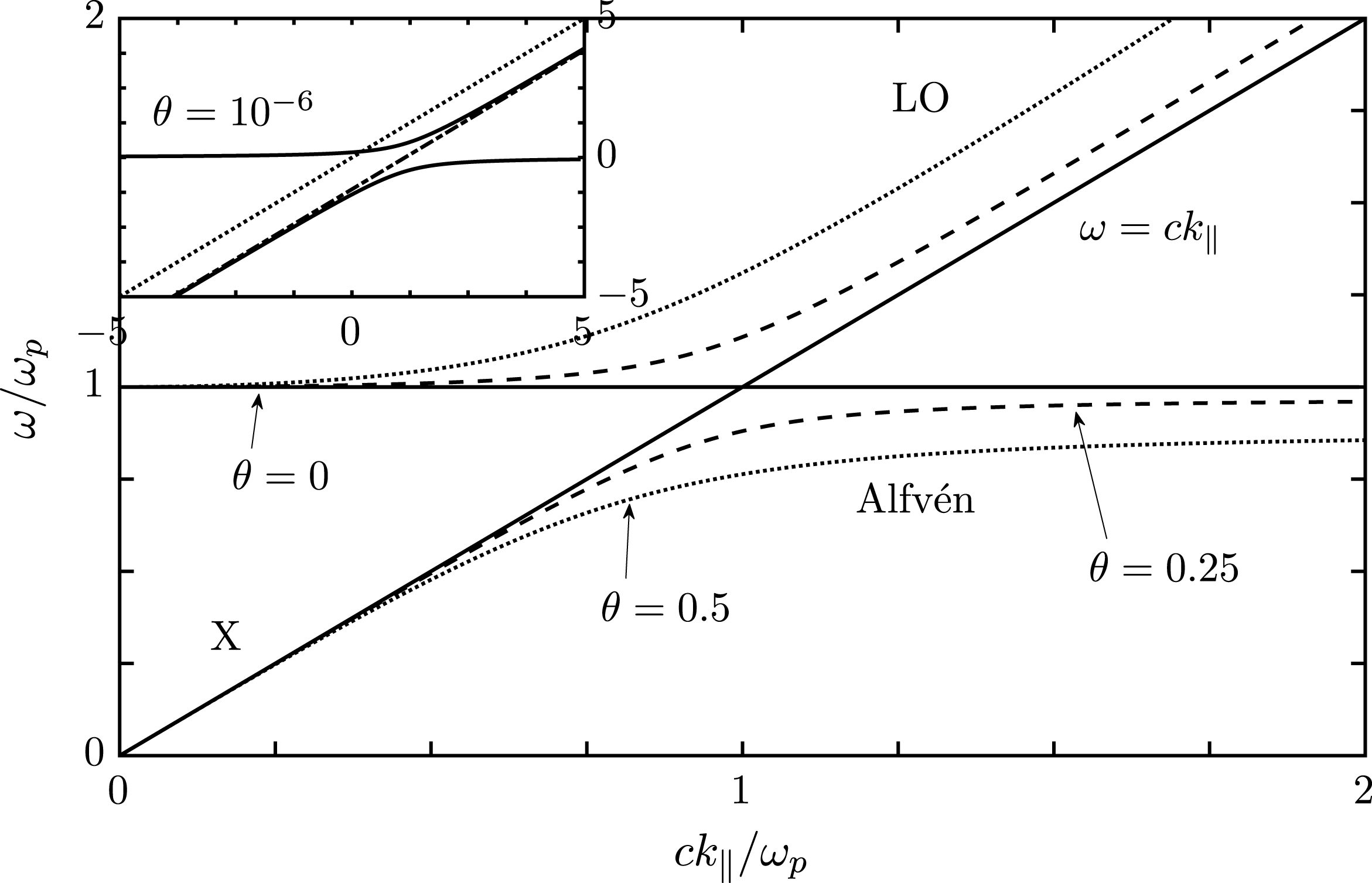
Figure 5. Wave properties in the cold limit. The axes of the inset are
![]() $(\unicode[STIX]{x1D714}/\unicode[STIX]{x1D714}_{\text{p}}-1)\times 10^{6}$
and
$(\unicode[STIX]{x1D714}/\unicode[STIX]{x1D714}_{\text{p}}-1)\times 10^{6}$
and
![]() $(ck_{\Vert }/\unicode[STIX]{x1D714}_{\text{p}}-1)\times 10^{6}$
. The dotted line in the inset is the light line,
$(ck_{\Vert }/\unicode[STIX]{x1D714}_{\text{p}}-1)\times 10^{6}$
. The dotted line in the inset is the light line,
![]() $z=1$
, and the dashed line is the X mode.
$z=1$
, and the dashed line is the X mode.
4.1.4 Cross-over frequency
The dispersion relations for the A and L modes for strictly parallel propagation cross each other at the cross-over frequency
A cross-over always occurs in the cold-plasma limit, for which the dispersion relations reduce to the horizontal line,
![]() $\unicode[STIX]{x1D714}=\unicode[STIX]{x1D714}_{\text{p}}$
(L mode), and the oblique line,
$\unicode[STIX]{x1D714}=\unicode[STIX]{x1D714}_{\text{p}}$
(L mode), and the oblique line,
![]() $z=z_{\text{A}}$
(A and X modes) that passes through the origin in the
$z=z_{\text{A}}$
(A and X modes) that passes through the origin in the
![]() $\unicode[STIX]{x1D714}$
-
$\unicode[STIX]{x1D714}$
-
![]() $z$
plane.
$z$
plane.
4.2 Dispersion curves for
 $\unicode[STIX]{x1D70C}=20$
$\unicode[STIX]{x1D70C}=20$
The transition from the cold-plasma limit,
![]() $\unicode[STIX]{x1D70C}\rightarrow \infty$
, to the highly relativistic limit,
$\unicode[STIX]{x1D70C}\rightarrow \infty$
, to the highly relativistic limit,
![]() $\unicode[STIX]{x1D70C}\ll 1$
, leads to a dramatic change in the wave properties. To follow how this transition occurs, it is helpful to consider two intermediate cases: one where thermal effects are significant and relativistic effects are small, and another where relativistic effects are important. We choose the intermediate cases
$\unicode[STIX]{x1D70C}\ll 1$
, leads to a dramatic change in the wave properties. To follow how this transition occurs, it is helpful to consider two intermediate cases: one where thermal effects are significant and relativistic effects are small, and another where relativistic effects are important. We choose the intermediate cases
![]() $\unicode[STIX]{x1D70C}=20$
and
$\unicode[STIX]{x1D70C}=20$
and
![]() $\unicode[STIX]{x1D70C}=1$
.
$\unicode[STIX]{x1D70C}=1$
.
4.2.1 L mode for
 $\unicode[STIX]{x1D70C}=20$
$\unicode[STIX]{x1D70C}=20$
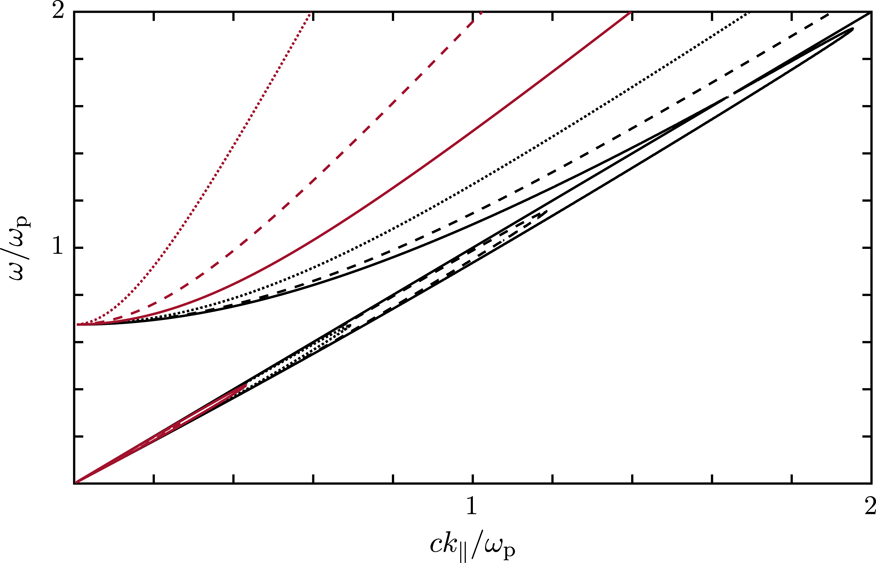
The dispersion curves are illustrated for
![]() $\unicode[STIX]{x1D70C}=20$
in figure 6. The dispersion relation for the L mode changes from the horizontal line
$\unicode[STIX]{x1D70C}=20$
in figure 6. The dispersion relation for the L mode changes from the horizontal line
![]() $\unicode[STIX]{x1D714}=\unicode[STIX]{x1D714}_{\text{p}}$
in a cold plasma to the solid black curve in figure 6, which may be regarded as a plot of
$\unicode[STIX]{x1D714}=\unicode[STIX]{x1D714}_{\text{p}}$
in a cold plasma to the solid black curve in figure 6, which may be regarded as a plot of
![]() $\unicode[STIX]{x1D714}/\unicode[STIX]{x1D714}_{\text{p}}$
versus
$\unicode[STIX]{x1D714}/\unicode[STIX]{x1D714}_{\text{p}}$
versus
![]() $ck_{\Vert }/\unicode[STIX]{x1D714}_{\text{p}}=(\unicode[STIX]{x1D714}/\unicode[STIX]{x1D714}_{\text{p}})/z$
. The cutoff frequency,
$ck_{\Vert }/\unicode[STIX]{x1D714}_{\text{p}}=(\unicode[STIX]{x1D714}/\unicode[STIX]{x1D714}_{\text{p}})/z$
. The cutoff frequency,
![]() $\unicode[STIX]{x1D714}_{x}=\unicode[STIX]{x1D714}_{\text{L}}(\infty )=\langle 1/\unicode[STIX]{x1D6FE}^{3}\rangle \unicode[STIX]{x1D714}_{\text{p}}$
, moves to just below
$\unicode[STIX]{x1D714}_{x}=\unicode[STIX]{x1D714}_{\text{L}}(\infty )=\langle 1/\unicode[STIX]{x1D6FE}^{3}\rangle \unicode[STIX]{x1D714}_{\text{p}}$
, moves to just below
![]() $\unicode[STIX]{x1D714}_{\text{p}}$
due to a relativistic correction
$\unicode[STIX]{x1D714}_{\text{p}}$
due to a relativistic correction
![]() $\langle 1/\unicode[STIX]{x1D6FE}^{3}\rangle$
. The frequency increases with increasing
$\langle 1/\unicode[STIX]{x1D6FE}^{3}\rangle$
. The frequency increases with increasing
![]() $k_{\Vert }$
, crosses the light line at
$k_{\Vert }$
, crosses the light line at
![]() $\unicode[STIX]{x1D714}_{1}=\unicode[STIX]{x1D714}_{\text{L}}(1)=(2\langle \unicode[STIX]{x1D6FE}\rangle -\langle 1/\unicode[STIX]{x1D6FE}\rangle )\unicode[STIX]{x1D714}_{\text{p}}$
,
$\unicode[STIX]{x1D714}_{1}=\unicode[STIX]{x1D714}_{\text{L}}(1)=(2\langle \unicode[STIX]{x1D6FE}\rangle -\langle 1/\unicode[STIX]{x1D6FE}\rangle )\unicode[STIX]{x1D714}_{\text{p}}$
,
![]() $k_{\Vert }c=\unicode[STIX]{x1D714}_{1}$
and reaches its maximum at
$k_{\Vert }c=\unicode[STIX]{x1D714}_{1}$
and reaches its maximum at
![]() $z=z_{\text{m}}$
, corresponding to
$z=z_{\text{m}}$
, corresponding to
![]() $\unicode[STIX]{x1D714}/\unicode[STIX]{x1D714}_{\text{p}}\approx 1.5$
and
$\unicode[STIX]{x1D714}/\unicode[STIX]{x1D714}_{\text{p}}\approx 1.5$
and
![]() $ck_{\Vert }/\unicode[STIX]{x1D714}_{\text{p}}=2.6$
.
$ck_{\Vert }/\unicode[STIX]{x1D714}_{\text{p}}=2.6$
.

Figure 6. Dispersion curves for
![]() $\unicode[STIX]{x1D70C}=20$
. The solid black curves correspond to the L and A modes for
$\unicode[STIX]{x1D70C}=20$
. The solid black curves correspond to the L and A modes for
![]() $\unicode[STIX]{x1D703}=0$
, and the other nested curves are for the O and Alfvén modes with
$\unicode[STIX]{x1D703}=0$
, and the other nested curves are for the O and Alfvén modes with
![]() $\unicode[STIX]{x1D703}$
increasing in steps of 0.25 rad. The X mode (not shown) is degenerate with the A mode for
$\unicode[STIX]{x1D703}$
increasing in steps of 0.25 rad. The X mode (not shown) is degenerate with the A mode for
![]() $\unicode[STIX]{x1D703}=0$
.
$\unicode[STIX]{x1D703}=0$
.
The L mode is double valued, with a higher-frequency portion and a lower-frequency portion joining at what we refer to as a turnover. The turnover, as a function of
![]() $z$
, occurs at
$z$
, occurs at
![]() $z=z_{\text{m}}$
, where the RPDF has its maximum. The lower-frequency portion of the dispersion curve extends to
$z=z_{\text{m}}$
, where the RPDF has its maximum. The lower-frequency portion of the dispersion curve extends to
![]() $\unicode[STIX]{x1D714}=0$
, which is approached along the line
$\unicode[STIX]{x1D714}=0$
, which is approached along the line
![]() $z=z_{0}$
(or
$z=z_{0}$
(or
![]() $\unicode[STIX]{x1D714}/\unicode[STIX]{x1D714}_{\text{p}}=z_{0}ck_{\Vert }/\unicode[STIX]{x1D714}_{\text{p}}$
), where the RPDF passes through zero. The higher-frequency portion may be interpreted as a counterpart of the parallel Langmuir mode in a non-relativistic, magnetized plasma; the L mode dispersion relation (2.3) may be approximated by
$\unicode[STIX]{x1D714}/\unicode[STIX]{x1D714}_{\text{p}}=z_{0}ck_{\Vert }/\unicode[STIX]{x1D714}_{\text{p}}$
), where the RPDF passes through zero. The higher-frequency portion may be interpreted as a counterpart of the parallel Langmuir mode in a non-relativistic, magnetized plasma; the L mode dispersion relation (2.3) may be approximated by
![]() $\unicode[STIX]{x1D714}_{\text{L}}^{2}(z)=\unicode[STIX]{x1D714}_{\text{p}}^{2}+3k_{\Vert }^{2}V^{2}$
with
$\unicode[STIX]{x1D714}_{\text{L}}^{2}(z)=\unicode[STIX]{x1D714}_{\text{p}}^{2}+3k_{\Vert }^{2}V^{2}$
with
![]() $\unicode[STIX]{x1D70C}=c^{2}/V^{2}\gg 1$
. The lower-frequency portion of the dispersion curve is in a region of strong Landau damping, and we do not discuss this branch further.
$\unicode[STIX]{x1D70C}=c^{2}/V^{2}\gg 1$
. The lower-frequency portion of the dispersion curve is in a region of strong Landau damping, and we do not discuss this branch further.
4.2.2 Cross-over of the A and L modes
The solid black line in figure 6 is the dispersion relation
![]() $z=z_{\text{A}}$
for the (parallel Alfvén or) A mode, which is at an angle
$z=z_{\text{A}}$
for the (parallel Alfvén or) A mode, which is at an angle
![]() $\unicode[STIX]{x1D713}_{\text{A}}=\arctan z_{\text{A}}$
to the horizontal. For the value of
$\unicode[STIX]{x1D713}_{\text{A}}=\arctan z_{\text{A}}$
to the horizontal. For the value of
![]() $\unicode[STIX]{x1D6FD}_{\text{A}}\approx 2.1\times 10^{2}$
chosen in the plot
$\unicode[STIX]{x1D6FD}_{\text{A}}\approx 2.1\times 10^{2}$
chosen in the plot
![]() $\unicode[STIX]{x1D713}_{\text{A}}\approx \unicode[STIX]{x03C0}/4$
and this line is indistinguishable from the light line. For this large value of
$\unicode[STIX]{x1D713}_{\text{A}}\approx \unicode[STIX]{x03C0}/4$
and this line is indistinguishable from the light line. For this large value of
![]() $\unicode[STIX]{x1D6FD}_{\text{A}}$
the cross-over frequency cannot be distinguished from the frequency
$\unicode[STIX]{x1D6FD}_{\text{A}}$
the cross-over frequency cannot be distinguished from the frequency
![]() $\unicode[STIX]{x1D714}_{1}=\unicode[STIX]{x1D714}_{\text{L}}(1)$
in figure 6. For smaller values of
$\unicode[STIX]{x1D714}_{1}=\unicode[STIX]{x1D714}_{\text{L}}(1)$
in figure 6. For smaller values of
![]() $\unicode[STIX]{x1D6FD}_{\text{A}}$
the cross-over point is on the higher-frequency portion of the curve for
$\unicode[STIX]{x1D6FD}_{\text{A}}$
the cross-over point is on the higher-frequency portion of the curve for
![]() $z_{\text{A}}>z_{\text{m}}$
, on the lower-frequency portion of the curve for
$z_{\text{A}}>z_{\text{m}}$
, on the lower-frequency portion of the curve for
![]() $z_{\text{m}}>z_{\text{A}}>z_{0}$
and there is no cross-over for
$z_{\text{m}}>z_{\text{A}}>z_{0}$
and there is no cross-over for
![]() $z_{\text{A}}<z_{0}$
. In the following discussion we assume
$z_{\text{A}}<z_{0}$
. In the following discussion we assume
![]() $z_{\text{A}}>z_{\text{m}}$
, except where we discuss the other two cases explicitly.
$z_{\text{A}}>z_{\text{m}}$
, except where we discuss the other two cases explicitly.
4.2.3 Oblique O and Alfvén modes for
 $\unicode[STIX]{x1D70C}=20$
$\unicode[STIX]{x1D70C}=20$
For
![]() $\tan \unicode[STIX]{x1D703}\neq 0$
the L and A modes reconnect to form the O mode, which moves to the upper left as
$\tan \unicode[STIX]{x1D703}\neq 0$
the L and A modes reconnect to form the O mode, which moves to the upper left as
![]() $\unicode[STIX]{x1D703}$
increases, and the Alfvén mode, which moves to the lower right as
$\unicode[STIX]{x1D703}$
increases, and the Alfvén mode, which moves to the lower right as
![]() $\unicode[STIX]{x1D703}$
increases. The turnover, corresponding to the peak in the RPDF, is in the Alfvén mode for
$\unicode[STIX]{x1D703}$
increases. The turnover, corresponding to the peak in the RPDF, is in the Alfvén mode for
![]() $z_{\text{A}}>z_{\text{m}}$
. The reconnected Alfvén mode consists of two branches, and for sufficiently small
$z_{\text{A}}>z_{\text{m}}$
. The reconnected Alfvén mode consists of two branches, and for sufficiently small
![]() $\unicode[STIX]{x1D703}$
, these are the familiar Alfvén mode with
$\unicode[STIX]{x1D703}$
, these are the familiar Alfvén mode with
![]() $z\approx z_{\text{A}}$
,
$z\approx z_{\text{A}}$
,
![]() $\unicode[STIX]{x1D714}<\unicode[STIX]{x1D714}_{\text{co}}$
, and a branch that follows the L mode for
$\unicode[STIX]{x1D714}<\unicode[STIX]{x1D714}_{\text{co}}$
, and a branch that follows the L mode for
![]() $z_{\text{A}}>z\gtrsim z_{\text{m}}$
. We refer to the latter as the turnover branch. The wave properties remain topologically similar as
$z_{\text{A}}>z\gtrsim z_{\text{m}}$
. We refer to the latter as the turnover branch. The wave properties remain topologically similar as
![]() $\unicode[STIX]{x1D70C}$
decreases, but become increasingly distorted from the mildly relativistic case
$\unicode[STIX]{x1D70C}$
decreases, but become increasingly distorted from the mildly relativistic case
![]() $\unicode[STIX]{x1D70C}=20$
as
$\unicode[STIX]{x1D70C}=20$
as
![]() $\unicode[STIX]{x1D70C}$
decreases to
$\unicode[STIX]{x1D70C}$
decreases to
![]() ${\lesssim}1$
.
${\lesssim}1$
.
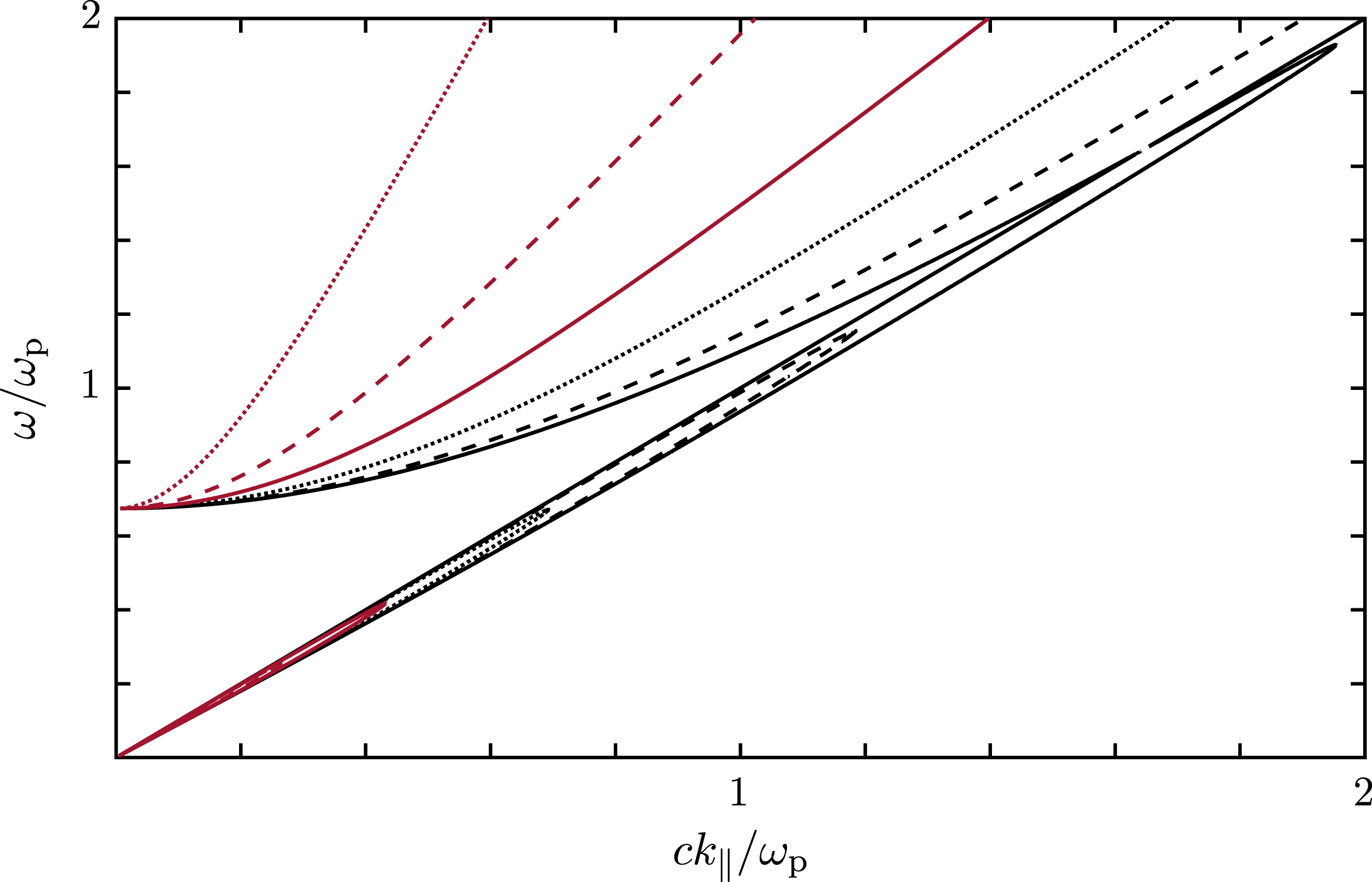
Figure 7. Dispersion curves for
![]() $\unicode[STIX]{x1D70C}=1$
in the same form as figure 6.
$\unicode[STIX]{x1D70C}=1$
in the same form as figure 6.
4.3 Dispersion curves for
 $\unicode[STIX]{x1D70C}=1$
$\unicode[STIX]{x1D70C}=1$
For the case
![]() $\unicode[STIX]{x1D70C}=1$
shown in figure 7, relativistic effects are important. Comparing the dispersion curves in figure 7 with those in figure 6, an obvious difference is the cutoff frequency
$\unicode[STIX]{x1D70C}=1$
shown in figure 7, relativistic effects are important. Comparing the dispersion curves in figure 7 with those in figure 6, an obvious difference is the cutoff frequency
![]() $\unicode[STIX]{x1D714}_{x}=\unicode[STIX]{x1D714}_{\text{L}}(\infty )$
, which is only marginally below
$\unicode[STIX]{x1D714}_{x}=\unicode[STIX]{x1D714}_{\text{L}}(\infty )$
, which is only marginally below
![]() $\unicode[STIX]{x1D714}=\unicode[STIX]{x1D714}_{\text{p}}$
for
$\unicode[STIX]{x1D714}=\unicode[STIX]{x1D714}_{\text{p}}$
for
![]() $\unicode[STIX]{x1D70C}=20$
, and is significantly below
$\unicode[STIX]{x1D70C}=20$
, and is significantly below
![]() $\unicode[STIX]{x1D714}=\unicode[STIX]{x1D714}_{\text{p}}$
for
$\unicode[STIX]{x1D714}=\unicode[STIX]{x1D714}_{\text{p}}$
for
![]() $\unicode[STIX]{x1D70C}=1$
. Another notable difference is the frequency
$\unicode[STIX]{x1D70C}=1$
. Another notable difference is the frequency
![]() $\unicode[STIX]{x1D714}_{1}=\unicode[STIX]{x1D714}_{\text{L}}(1)$
at which the dispersion curve for the L mode crosses the light line: this is marginally above
$\unicode[STIX]{x1D714}_{1}=\unicode[STIX]{x1D714}_{\text{L}}(1)$
at which the dispersion curve for the L mode crosses the light line: this is marginally above
![]() $\unicode[STIX]{x1D714}=\unicode[STIX]{x1D714}_{\text{p}}$
for
$\unicode[STIX]{x1D714}=\unicode[STIX]{x1D714}_{\text{p}}$
for
![]() $\unicode[STIX]{x1D70C}=20$
, and significantly above
$\unicode[STIX]{x1D70C}=20$
, and significantly above
![]() $\unicode[STIX]{x1D714}=\unicode[STIX]{x1D714}_{\text{p}}$
for
$\unicode[STIX]{x1D714}=\unicode[STIX]{x1D714}_{\text{p}}$
for
![]() $\unicode[STIX]{x1D70C}=1$
. A further difference is a narrowing of the dispersion curve for the (reconnected) Alfvén mode, with the higher-frequency and lower-frequency portions of the dispersion curves moving closer together and closer to the light line. These intrinsically relativistic features become increasingly important as
$\unicode[STIX]{x1D70C}=1$
. A further difference is a narrowing of the dispersion curve for the (reconnected) Alfvén mode, with the higher-frequency and lower-frequency portions of the dispersion curves moving closer together and closer to the light line. These intrinsically relativistic features become increasingly important as
![]() $\unicode[STIX]{x1D70C}$
decreases to
$\unicode[STIX]{x1D70C}$
decreases to
![]() $\ll 1$
.
$\ll 1$
.
5 Wave dispersion for
 $\unicode[STIX]{x1D70C}\ll 1$
$\unicode[STIX]{x1D70C}\ll 1$
In this section we discuss the wave properties for a pulsar plasma with
![]() $\unicode[STIX]{x1D70C}\ll 1$
, corresponding to
$\unicode[STIX]{x1D70C}\ll 1$
, corresponding to
![]() $\langle \unicode[STIX]{x1D6FE}\rangle \approx 1/\unicode[STIX]{x1D70C}\gg 1$
.
$\langle \unicode[STIX]{x1D6FE}\rangle \approx 1/\unicode[STIX]{x1D70C}\gg 1$
.
5.1 L mode for
 $\langle \unicode[STIX]{x1D6FE}\rangle \gg 1$
$\langle \unicode[STIX]{x1D6FE}\rangle \gg 1$
Approximate forms for the dispersion relation for the L mode, given by (2.3), for large
![]() $z$
and for
$z$
and for
![]() $z\approx 1$
, were given in the early literature (Lominadze & Mikhailovskiǐ Reference Lominadze and Mikhailovskiǐ1979; Lominadze et al.
Reference Lominadze, Mikhaǐlovskiǐ and Sagdeev1979). These approximations are derived by expanding
$z\approx 1$
, were given in the early literature (Lominadze & Mikhailovskiǐ Reference Lominadze and Mikhailovskiǐ1979; Lominadze et al.
Reference Lominadze, Mikhaǐlovskiǐ and Sagdeev1979). These approximations are derived by expanding
![]() $z^{2}W(z)$
in powers of
$z^{2}W(z)$
in powers of
![]() $1/z\ll 1$
and in powers of
$1/z\ll 1$
and in powers of
![]() $|1-z|\ll 1$
, respectively, and retaining only the lowest-order terms,
$|1-z|\ll 1$
, respectively, and retaining only the lowest-order terms,
 $$\begin{eqnarray}\displaystyle z^{2}W(z)\approx \left\{\begin{array}{@{}ll@{}}\displaystyle \left\langle {\displaystyle \frac{1}{\unicode[STIX]{x1D6FE}^{3}}}\right\rangle \left[1+{\displaystyle \frac{3}{z^{2}}}\left(1-{\displaystyle \frac{\langle \unicode[STIX]{x1D6FE}^{-5}\rangle }{\langle \unicode[STIX]{x1D6FE}^{-3}\rangle }}\right)\right]\approx {\displaystyle \frac{1}{\langle \unicode[STIX]{x1D6FE}\rangle }}\left(1+{\displaystyle \frac{3}{z^{2}}}\right),\quad & \text{for}~|z|\gg 1,\\[11.0pt] 2\langle \unicode[STIX]{x1D6FE}\rangle +(z^{2}-1)4\langle \unicode[STIX]{x1D6FE}^{3}\rangle \approx 2\langle \unicode[STIX]{x1D6FE}\rangle [1+12(z^{2}-1)\langle \unicode[STIX]{x1D6FE}\rangle ^{2}],\quad & \text{for}~|1-z^{2}|\ll 1,\end{array}\right. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle z^{2}W(z)\approx \left\{\begin{array}{@{}ll@{}}\displaystyle \left\langle {\displaystyle \frac{1}{\unicode[STIX]{x1D6FE}^{3}}}\right\rangle \left[1+{\displaystyle \frac{3}{z^{2}}}\left(1-{\displaystyle \frac{\langle \unicode[STIX]{x1D6FE}^{-5}\rangle }{\langle \unicode[STIX]{x1D6FE}^{-3}\rangle }}\right)\right]\approx {\displaystyle \frac{1}{\langle \unicode[STIX]{x1D6FE}\rangle }}\left(1+{\displaystyle \frac{3}{z^{2}}}\right),\quad & \text{for}~|z|\gg 1,\\[11.0pt] 2\langle \unicode[STIX]{x1D6FE}\rangle +(z^{2}-1)4\langle \unicode[STIX]{x1D6FE}^{3}\rangle \approx 2\langle \unicode[STIX]{x1D6FE}\rangle [1+12(z^{2}-1)\langle \unicode[STIX]{x1D6FE}\rangle ^{2}],\quad & \text{for}~|1-z^{2}|\ll 1,\end{array}\right. & & \displaystyle\end{eqnarray}$$
where the final forms apply for a Jüttner distribution with
![]() $\langle \unicode[STIX]{x1D6FE}\rangle \gg 1$
(Melrose & Gedalin Reference Melrose and Gedalin1999),
$\langle \unicode[STIX]{x1D6FE}\rangle \gg 1$
(Melrose & Gedalin Reference Melrose and Gedalin1999),
We rederive the approximations (5.1) in appendix D by expanding in powers of
![]() $1/z^{2}$
and
$1/z^{2}$
and
![]() $z-1$
, respectively. Although we find that the approximation for
$z-1$
, respectively. Although we find that the approximation for
![]() $z^{2}\gg 1$
is well justified, that for
$z^{2}\gg 1$
is well justified, that for
![]() $z-1$
is based on an expansion that converges only for
$z-1$
is based on an expansion that converges only for
![]() $z^{2}=1$
. We suggest that the approximation (5.1) for
$z^{2}=1$
. We suggest that the approximation (5.1) for
![]() $|1-z^{2}|\ll 1$
should not be used, at least without further justification.
$|1-z^{2}|\ll 1$
should not be used, at least without further justification.
The cutoff frequency
![]() $\unicode[STIX]{x1D714}_{x}$
and the frequency
$\unicode[STIX]{x1D714}_{x}$
and the frequency
![]() $\unicode[STIX]{x1D714}_{1}$
are given by
$\unicode[STIX]{x1D714}_{1}$
are given by
with
![]() $\langle 1/\unicode[STIX]{x1D6FE}^{3}\rangle \approx 1/\langle \unicode[STIX]{x1D6FE}\rangle$
for
$\langle 1/\unicode[STIX]{x1D6FE}^{3}\rangle \approx 1/\langle \unicode[STIX]{x1D6FE}\rangle$
for
![]() $\langle \unicode[STIX]{x1D6FE}\rangle \gg 1$
. For a cold plasma one obtains
$\langle \unicode[STIX]{x1D6FE}\rangle \gg 1$
. For a cold plasma one obtains
![]() $\unicode[STIX]{x1D714}_{x}=\unicode[STIX]{x1D714}_{1}=\unicode[STIX]{x1D714}_{\text{p}}$
.
$\unicode[STIX]{x1D714}_{x}=\unicode[STIX]{x1D714}_{1}=\unicode[STIX]{x1D714}_{\text{p}}$
.
The dispersion relation,
![]() $\unicode[STIX]{x1D714}=\unicode[STIX]{x1D714}_{\text{L}}(z)$
, just above the cutoff frequency
$\unicode[STIX]{x1D714}=\unicode[STIX]{x1D714}_{\text{L}}(z)$
, just above the cutoff frequency
![]() $\unicode[STIX]{x1D714}_{x}$
is then given by
$\unicode[STIX]{x1D714}_{x}$
is then given by
which reproduces a known result (Lominadze & Mikhailovskiǐ Reference Lominadze and Mikhailovskiǐ1979; Lominadze et al.
Reference Lominadze, Mikhaǐlovskiǐ and Sagdeev1979; Melrose & Gedalin Reference Melrose and Gedalin1999). However, analogous approximate dispersion relations for
![]() $z^{2}\approx 1$
are questionable for the reason discussed above. Specifically, although one can evaluate
$z^{2}\approx 1$
are questionable for the reason discussed above. Specifically, although one can evaluate
![]() $z^{2}W(z)$
and all its derivatives at
$z^{2}W(z)$
and all its derivatives at
![]() $z^{2}=1$
, the Taylor series in
$z^{2}=1$
, the Taylor series in
![]() $(z^{2}-1)$
involving these derivatives appears to have zero radius of convergence (appendix D).
$(z^{2}-1)$
involving these derivatives appears to have zero radius of convergence (appendix D).
5.2 O mode for
 $\langle \unicode[STIX]{x1D6FE}\rangle \gg 1$
$\langle \unicode[STIX]{x1D6FE}\rangle \gg 1$
The O mode has the same cutoff frequency,
![]() $\unicode[STIX]{x1D714}_{x}$
, as the L mode independent of
$\unicode[STIX]{x1D714}_{x}$
, as the L mode independent of
![]() $\unicode[STIX]{x1D703}$
. As
$\unicode[STIX]{x1D703}$
. As
![]() $\unicode[STIX]{x1D703}$
increases the dispersion curve for the O mode deviates increasingly from that of the L mode frequency. One may rewrite (2.5) in the form
$\unicode[STIX]{x1D703}$
increases the dispersion curve for the O mode deviates increasingly from that of the L mode frequency. One may rewrite (2.5) in the form
One has
![]() $z^{2}>z_{\text{A}}^{2}+b\tan ^{2}\unicode[STIX]{x1D703}$
for the O mode, and hence
$z^{2}>z_{\text{A}}^{2}+b\tan ^{2}\unicode[STIX]{x1D703}$
for the O mode, and hence
![]() $a(z)<0$
, which implies that the frequency is an increasing function of
$a(z)<0$
, which implies that the frequency is an increasing function of
![]() $\unicode[STIX]{x1D703}$
. Except for the small range
$\unicode[STIX]{x1D703}$
. Except for the small range
![]() $\unicode[STIX]{x1D703}^{2}\lesssim 2/\unicode[STIX]{x1D6FD}_{\text{A}}^{2}$
the dispersion curve for the O mode is entirely in the superluminal range. The resonance condition
$\unicode[STIX]{x1D703}^{2}\lesssim 2/\unicode[STIX]{x1D6FD}_{\text{A}}^{2}$
the dispersion curve for the O mode is entirely in the superluminal range. The resonance condition
![]() $\unicode[STIX]{x1D6FD}_{\text{s}}=z$
, where
$\unicode[STIX]{x1D6FD}_{\text{s}}=z$
, where
![]() $\unicode[STIX]{x1D6FD}_{\text{s}}c$
is the streaming speed, cannot be satisfied for the O mode except for this tiny range of angles. An approximate dispersion relation for the (superluminal) O mode follows by setting
$\unicode[STIX]{x1D6FD}_{\text{s}}c$
is the streaming speed, cannot be satisfied for the O mode except for this tiny range of angles. An approximate dispersion relation for the (superluminal) O mode follows by setting
![]() $z_{\text{A}}^{2}\rightarrow 1$
,
$z_{\text{A}}^{2}\rightarrow 1$
,
![]() $b\rightarrow 1$
in (5.5),
$b\rightarrow 1$
in (5.5),
which applies for
![]() $z^{2}>1$
when
$z^{2}>1$
when
![]() $\unicode[STIX]{x1D6FD}_{\text{A}}^{2}\gg 1$
. The frequency,
$\unicode[STIX]{x1D6FD}_{\text{A}}^{2}\gg 1$
. The frequency,
![]() $\unicode[STIX]{x1D714}_{\text{O}}(1,\unicode[STIX]{x1D703})$
, at which the dispersion curve crosses the light line increases with increasing
$\unicode[STIX]{x1D714}_{\text{O}}(1,\unicode[STIX]{x1D703})$
, at which the dispersion curve crosses the light line increases with increasing
![]() $\unicode[STIX]{x1D703}$
,
$\unicode[STIX]{x1D703}$
,
where the approximation applies for
![]() $\unicode[STIX]{x1D6FD}_{\text{A}}^{2}\gg 1$
,
$\unicode[STIX]{x1D6FD}_{\text{A}}^{2}\gg 1$
,
![]() $\langle \unicode[STIX]{x1D6FE}\rangle \gg 1$
and
$\langle \unicode[STIX]{x1D6FE}\rangle \gg 1$
and
![]() $\unicode[STIX]{x1D703}^{2}\ll 1$
.
$\unicode[STIX]{x1D703}^{2}\ll 1$
.
An approximate dispersion relation for the O mode for
![]() $z=1/N\cos \unicode[STIX]{x1D703}\gg 1$
and
$z=1/N\cos \unicode[STIX]{x1D703}\gg 1$
and
![]() $\unicode[STIX]{x1D714}^{2}\gg \unicode[STIX]{x1D714}_{\text{L}}^{2}(z=1/N\cos \unicode[STIX]{x1D703})$
that follows from (4.7) using (5.1) is
$\unicode[STIX]{x1D714}^{2}\gg \unicode[STIX]{x1D714}_{\text{L}}^{2}(z=1/N\cos \unicode[STIX]{x1D703})$
that follows from (4.7) using (5.1) is
where the final expression applies for
![]() $\unicode[STIX]{x1D714}^{2}\gg (1+3\cos ^{2}\unicode[STIX]{x1D703})\unicode[STIX]{x1D714}_{\text{p}}^{2}\sin ^{2}\unicode[STIX]{x1D703}/\langle \unicode[STIX]{x1D6FE}\rangle$
.
$\unicode[STIX]{x1D714}^{2}\gg (1+3\cos ^{2}\unicode[STIX]{x1D703})\unicode[STIX]{x1D714}_{\text{p}}^{2}\sin ^{2}\unicode[STIX]{x1D703}/\langle \unicode[STIX]{x1D6FE}\rangle$
.
5.3 Alfvén mode for
 $\langle \unicode[STIX]{x1D6FE}\rangle \gg 1$
$\langle \unicode[STIX]{x1D6FE}\rangle \gg 1$
The turnover branch of the Alfvén mode for
![]() $z_{\text{A}}>z_{\text{m}}$
and
$z_{\text{A}}>z_{\text{m}}$
and
![]() $\unicode[STIX]{x1D70C}\ll 1$
is dominated by the peak in
$\unicode[STIX]{x1D70C}\ll 1$
is dominated by the peak in
![]() $z^{2}W(z)$
. For the case
$z^{2}W(z)$
. For the case
![]() $\unicode[STIX]{x1D70C}=1$
shown in figure 7, the Alfvén mode consists of a thin loop, with the higher-frequency and lower-frequency portions joining at a turnover that corresponds to the peak at
$\unicode[STIX]{x1D70C}=1$
shown in figure 7, the Alfvén mode consists of a thin loop, with the higher-frequency and lower-frequency portions joining at a turnover that corresponds to the peak at
![]() $z=z_{\text{m}}$
in the RPDF. The maximum frequency of the Alfvén mode decreases with increasing
$z=z_{\text{m}}$
in the RPDF. The maximum frequency of the Alfvén mode decreases with increasing
![]() $\unicode[STIX]{x1D703}$
approximately along the line
$\unicode[STIX]{x1D703}$
approximately along the line
![]() $z=z_{\text{m}}$
. For
$z=z_{\text{m}}$
. For
![]() $\unicode[STIX]{x1D70C}\approx 1/\langle \unicode[STIX]{x1D6FE}\rangle \ll 1$
the loop becomes narrower with decreasing
$\unicode[STIX]{x1D70C}\approx 1/\langle \unicode[STIX]{x1D6FE}\rangle \ll 1$
the loop becomes narrower with decreasing
![]() $\unicode[STIX]{x1D70C}$
. The format adopted in figures 6 and 7 makes it increasingly difficult to illustrate the dispersive properties due to the curves being strongly concentrated near
$\unicode[STIX]{x1D70C}$
. The format adopted in figures 6 and 7 makes it increasingly difficult to illustrate the dispersive properties due to the curves being strongly concentrated near
![]() $z=1$
.
$z=1$
.
An alternative format is used in figure 8 to show the dispersion curves near
![]() $z=1$
: we plot
$z=1$
: we plot
![]() $\unicode[STIX]{x1D714}/\unicode[STIX]{x1D714}_{\text{p}}$
on a log scale as a function of
$\unicode[STIX]{x1D714}/\unicode[STIX]{x1D714}_{\text{p}}$
on a log scale as a function of
![]() $(1-z)/\unicode[STIX]{x1D70C}^{2}$
for
$(1-z)/\unicode[STIX]{x1D70C}^{2}$
for
![]() $\unicode[STIX]{x1D70C}=0.1$
, with
$\unicode[STIX]{x1D70C}=0.1$
, with
![]() $\unicode[STIX]{x1D6FD}_{\text{A}}\approx 1.2\times 10^{2}$
and
$\unicode[STIX]{x1D6FD}_{\text{A}}\approx 1.2\times 10^{2}$
and
![]() $\unicode[STIX]{x1D6FE}_{\text{A}}\approx 87$
, and
$\unicode[STIX]{x1D6FE}_{\text{A}}\approx 87$
, and
![]() $0.01$
, with
$0.01$
, with
![]() $\unicode[STIX]{x1D6FD}_{\text{A}}\approx 1.2\times 10^{3}$
and
$\unicode[STIX]{x1D6FD}_{\text{A}}\approx 1.2\times 10^{3}$
and
![]() $\unicode[STIX]{x1D6FE}_{\text{A}}\approx 8.7\times 10^{2}$
, where
$\unicode[STIX]{x1D6FE}_{\text{A}}\approx 8.7\times 10^{2}$
, where
![]() $\unicode[STIX]{x1D6FE}_{\text{A}}$
is defined by (A 12). The solid curves correspond to the L mode for
$\unicode[STIX]{x1D6FE}_{\text{A}}$
is defined by (A 12). The solid curves correspond to the L mode for
![]() $\unicode[STIX]{x1D703}=0$
and the solid vertical line is the dispersion curve
$\unicode[STIX]{x1D703}=0$
and the solid vertical line is the dispersion curve
![]() $z=z_{\text{A}}$
for the A mode. The curves to the left of
$z=z_{\text{A}}$
for the A mode. The curves to the left of
![]() $(1-z_{\text{A}})/\unicode[STIX]{x1D70C}^{2}$
correspond to the O mode and the curves to the right of
$(1-z_{\text{A}})/\unicode[STIX]{x1D70C}^{2}$
correspond to the O mode and the curves to the right of
![]() $(1-z_{\text{A}})/\unicode[STIX]{x1D70C}^{2}$
correspond to the Alfvén mode. Each of
$(1-z_{\text{A}})/\unicode[STIX]{x1D70C}^{2}$
correspond to the Alfvén mode. Each of
![]() $1-z_{\text{A}}\approx 1/2\unicode[STIX]{x1D6FD}_{\text{A}}^{2}$
,
$1-z_{\text{A}}\approx 1/2\unicode[STIX]{x1D6FD}_{\text{A}}^{2}$
,
![]() $1-z_{\text{m}}$
and
$1-z_{\text{m}}$
and
![]() $1-z_{0}$
is proportional to
$1-z_{0}$
is proportional to
![]() $\unicode[STIX]{x1D70C}^{2}\approx 1/\langle \unicode[STIX]{x1D6FE}\rangle ^{2}$
as discussed in § 3.3, so that the locations of the left asymptote, the peak and the right asymptote of the Alfvén mode all scale with
$\unicode[STIX]{x1D70C}^{2}\approx 1/\langle \unicode[STIX]{x1D6FE}\rangle ^{2}$
as discussed in § 3.3, so that the locations of the left asymptote, the peak and the right asymptote of the Alfvén mode all scale with
![]() $\unicode[STIX]{x1D70C}^{2}$
and so coincide in the two figures.
$\unicode[STIX]{x1D70C}^{2}$
and so coincide in the two figures.
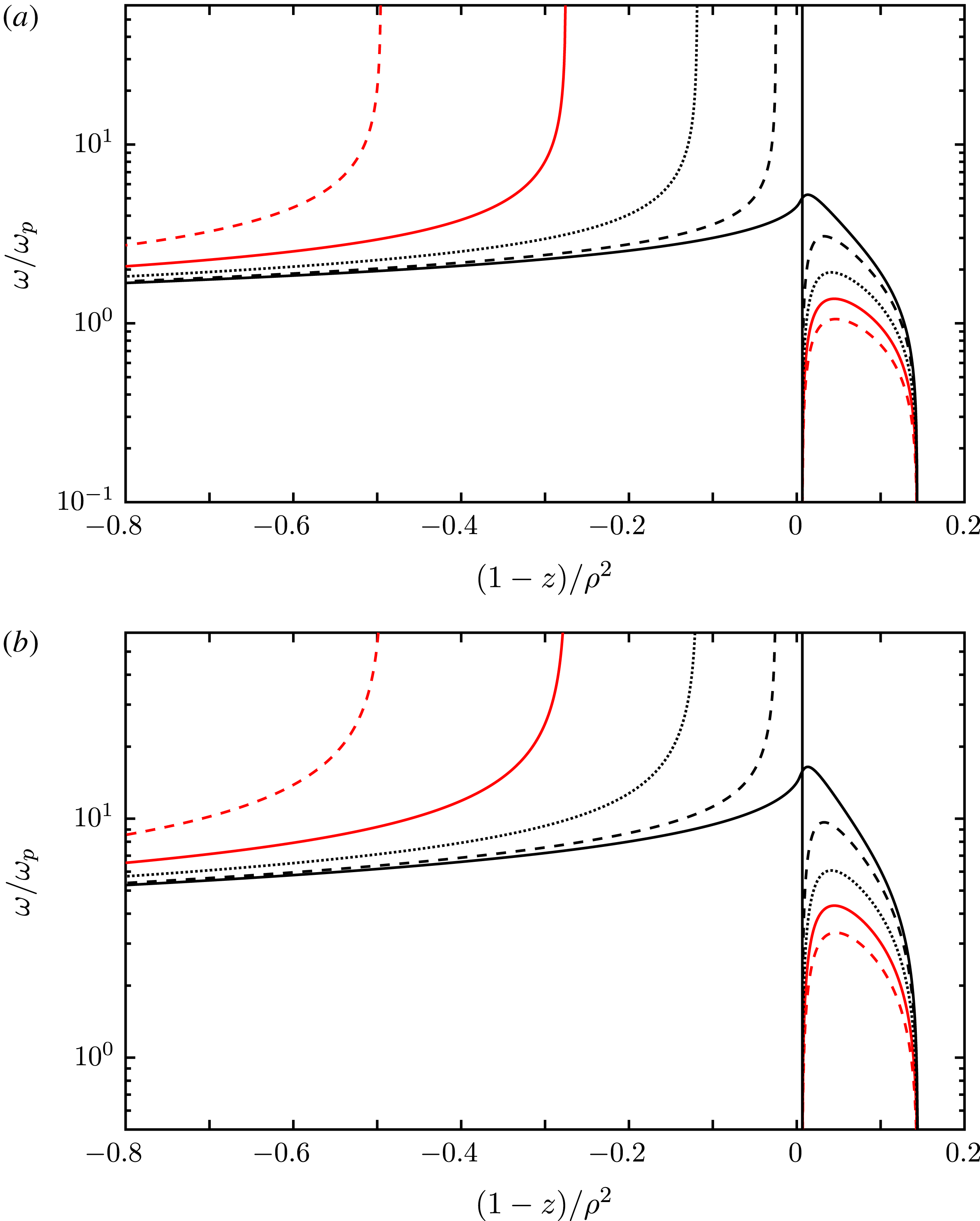
Figure 8. Dispersion curves for
![]() $\unicode[STIX]{x1D703}=0$
(black solid),
$\unicode[STIX]{x1D703}=0$
(black solid),
![]() $0.25\unicode[STIX]{x1D70C}$
rad (black dashed),
$0.25\unicode[STIX]{x1D70C}$
rad (black dashed),
![]() $0.5\unicode[STIX]{x1D70C}$
rad (black dotted),
$0.5\unicode[STIX]{x1D70C}$
rad (black dotted),
![]() $0.75\unicode[STIX]{x1D70C}$
rad (red solid) and
$0.75\unicode[STIX]{x1D70C}$
rad (red solid) and
![]() $0.1\unicode[STIX]{x1D70C}$
rad (red dashed): (a)
$0.1\unicode[STIX]{x1D70C}$
rad (red dashed): (a)
![]() $\unicode[STIX]{x1D70C}=0.1$
with
$\unicode[STIX]{x1D70C}=0.1$
with
![]() $\unicode[STIX]{x1D6FD}_{\text{A}}\approx 1.2\times 10^{2}$
, (b)
$\unicode[STIX]{x1D6FD}_{\text{A}}\approx 1.2\times 10^{2}$
, (b)
![]() $\unicode[STIX]{x1D70C}=0.01$
with
$\unicode[STIX]{x1D70C}=0.01$
with
![]() $\unicode[STIX]{x1D6FD}_{\text{A}}\approx 1.2\times 10^{3}$
. The black solid curve corresponds to the L mode, the solid vertical line at
$\unicode[STIX]{x1D6FD}_{\text{A}}\approx 1.2\times 10^{3}$
. The black solid curve corresponds to the L mode, the solid vertical line at
![]() $z=z_{\text{A}}$
corresponds to the A mode with the O mode to its upper left and the Alfvén mode to its lower right. The Alfvén mode exists between
$z=z_{\text{A}}$
corresponds to the A mode with the O mode to its upper left and the Alfvén mode to its lower right. The Alfvén mode exists between
![]() $z=z_{\text{A}}$
, which is very close to zero in the figure with
$z=z_{\text{A}}$
, which is very close to zero in the figure with
![]() $\unicode[STIX]{x1D6FE}_{\text{A}}\approx 87$
for
$\unicode[STIX]{x1D6FE}_{\text{A}}\approx 87$
for
![]() $\unicode[STIX]{x1D70C}=0.1$
and
$\unicode[STIX]{x1D70C}=0.1$
and
![]() $\unicode[STIX]{x1D6FE}_{\text{A}}=8.7\times 10^{2}$
for
$\unicode[STIX]{x1D6FE}_{\text{A}}=8.7\times 10^{2}$
for
![]() $\unicode[STIX]{x1D70C}=0.01$
, and
$\unicode[STIX]{x1D70C}=0.01$
, and
![]() $z=z_{0}$
. The maximum in the dispersion curve occurs near
$z=z_{0}$
. The maximum in the dispersion curve occurs near
![]() $z=z_{\text{m}}$
.
$z=z_{\text{m}}$
.
The Alfvén mode (for
![]() $\unicode[STIX]{x1D703}\neq 0$
) exists only for
$\unicode[STIX]{x1D703}\neq 0$
) exists only for
![]() $z<z_{\text{A}}$
or
$z<z_{\text{A}}$
or
![]() $\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D719}}<\unicode[STIX]{x1D6FE}_{\text{A}}\approx \unicode[STIX]{x1D6FD}_{\text{A}}$
. Its dispersion relation, given by (5.5) with
$\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D719}}<\unicode[STIX]{x1D6FE}_{\text{A}}\approx \unicode[STIX]{x1D6FD}_{\text{A}}$
. Its dispersion relation, given by (5.5) with
![]() $a(z)>0$
, becomes
$a(z)>0$
, becomes
The Alfvén mode is in the range where Landau damping is non-zero. Assuming that the waves are weakly damped only for
![]() $\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D719}}^{2}\gtrsim \unicode[STIX]{x1D6FE}_{\text{m}}^{2}$
, the approximations
$\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D719}}^{2}\gtrsim \unicode[STIX]{x1D6FE}_{\text{m}}^{2}$
, the approximations
![]() $z_{\text{m}}\approx 1-0.013\unicode[STIX]{x1D70C}^{2}$
, given by equation table 1, and
$z_{\text{m}}\approx 1-0.013\unicode[STIX]{x1D70C}^{2}$
, given by equation table 1, and
![]() $\langle \unicode[STIX]{x1D6FE}\rangle \approx 1/\unicode[STIX]{x1D70C}$
imply that the waves are weakly damped for
$\langle \unicode[STIX]{x1D6FE}\rangle \approx 1/\unicode[STIX]{x1D70C}$
imply that the waves are weakly damped for
![]() $\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D719}}\gtrsim 6\,\langle \unicode[STIX]{x1D6FE}\rangle$
.
$\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D719}}\gtrsim 6\,\langle \unicode[STIX]{x1D6FE}\rangle$
.
5.4 Condition for reconnection of modes
The dispersion curves for parallel propagation,
![]() $\unicode[STIX]{x1D714}=\unicode[STIX]{x1D714}_{\text{L}}(z)$
and
$\unicode[STIX]{x1D714}=\unicode[STIX]{x1D714}_{\text{L}}(z)$
and
![]() $z=z_{\text{A}}$
, do not necessarily cross in a relativistic plasma. There are three possibilities:
$z=z_{\text{A}}$
, do not necessarily cross in a relativistic plasma. There are three possibilities:
(i)
 $z_{\text{A}}>z_{\text{m}}$
: the line
$z_{\text{A}}>z_{\text{m}}$
: the line
 $z=z_{\text{A}}$
crosses the higher-frequency portion of the L mode dispersion curve
$z=z_{\text{A}}$
crosses the higher-frequency portion of the L mode dispersion curve
 $\unicode[STIX]{x1D714}=\unicode[STIX]{x1D714}_{\text{L}}(z)$
in the range
$\unicode[STIX]{x1D714}=\unicode[STIX]{x1D714}_{\text{L}}(z)$
in the range
 $1<z<z_{\text{m}}$
; reconnection in this case is similar to that in the cold-plasma limit. The peak in the dispersion curve is in the (reconnected) Alfvén mode.
$1<z<z_{\text{m}}$
; reconnection in this case is similar to that in the cold-plasma limit. The peak in the dispersion curve is in the (reconnected) Alfvén mode.(ii)
 $z_{\text{m}}>z_{\text{A}}>z_{0}$
: the line
$z_{\text{m}}>z_{\text{A}}>z_{0}$
: the line
 $z=z_{\text{A}}$
crosses the higher-frequency portion
$z=z_{\text{A}}$
crosses the higher-frequency portion
 $\unicode[STIX]{x1D714}=\unicode[STIX]{x1D714}_{\text{L}}(z)$
in the range
$\unicode[STIX]{x1D714}=\unicode[STIX]{x1D714}_{\text{L}}(z)$
in the range
 $z_{\text{m}}>z_{\text{A}}>z_{0}$
.
$z_{\text{m}}>z_{\text{A}}>z_{0}$
.(iii)
 $z_{\text{A}}<z_{0}$
: the line
$z_{\text{A}}<z_{0}$
: the line
 $z=z_{\text{A}}$
does not cross
$z=z_{\text{A}}$
does not cross
 $\unicode[STIX]{x1D714}=\unicode[STIX]{x1D714}_{\text{L}}(z)$
.
$\unicode[STIX]{x1D714}=\unicode[STIX]{x1D714}_{\text{L}}(z)$
.
Simple estimates for a pulsar magnetosphere suggest very large values,
![]() $\unicode[STIX]{x1D6FD}_{\text{A}}\gg 1$
, but before concentrating on this case we comment on the second and third cases.
$\unicode[STIX]{x1D6FD}_{\text{A}}\gg 1$
, but before concentrating on this case we comment on the second and third cases.
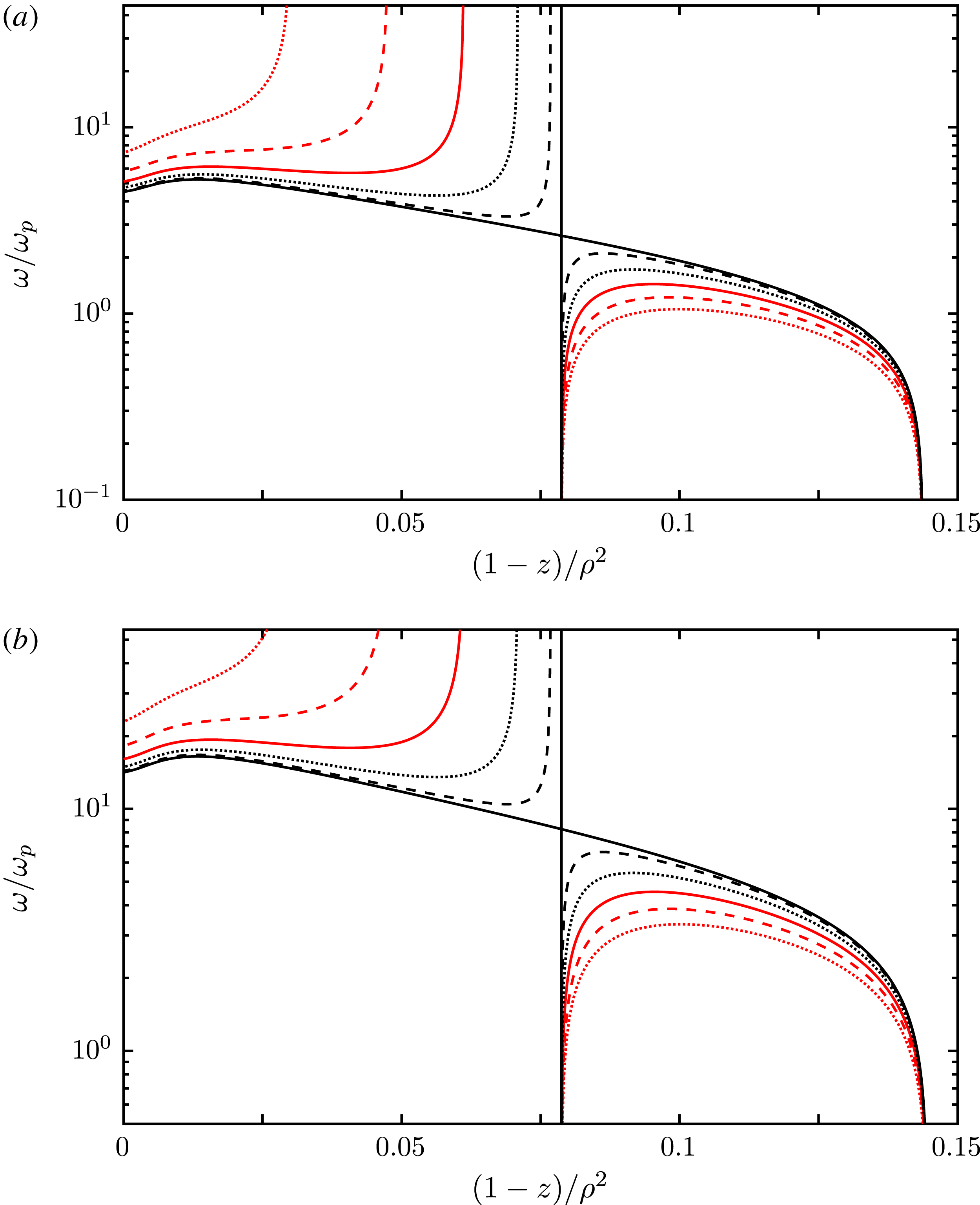
Figure 9. Similar to figure 8 but for
![]() $z_{\text{m}}>z_{\text{A}}>z_{0}$
and as a function of angle in steps of
$z_{\text{m}}>z_{\text{A}}>z_{0}$
and as a function of angle in steps of
![]() $0.0625\unicode[STIX]{x1D70C}$
rad: (a)
$0.0625\unicode[STIX]{x1D70C}$
rad: (a)
![]() $\unicode[STIX]{x1D70C}=0.1$
with
$\unicode[STIX]{x1D70C}=0.1$
with
![]() $\unicode[STIX]{x1D6FD}_{\text{A}}\approx 36$
and
$\unicode[STIX]{x1D6FD}_{\text{A}}\approx 36$
and
![]() $\unicode[STIX]{x1D6FE}_{\text{A}}\approx 25$
, (b)
$\unicode[STIX]{x1D6FE}_{\text{A}}\approx 25$
, (b)
![]() $\unicode[STIX]{x1D70C}=0.01$
with
$\unicode[STIX]{x1D70C}=0.01$
with
![]() $\unicode[STIX]{x1D6FD}_{\text{A}}\approx 3.6\times 10^{2}$
and
$\unicode[STIX]{x1D6FD}_{\text{A}}\approx 3.6\times 10^{2}$
and
![]() $\unicode[STIX]{x1D6FE}_{\text{A}}\approx 2.5\times 10^{2}$
.
$\unicode[STIX]{x1D6FE}_{\text{A}}\approx 2.5\times 10^{2}$
.
5.4.1 Case
 $z_{\text{m}}>z_{\text{A}}>z_{0}$
$z_{\text{m}}>z_{\text{A}}>z_{0}$
Examples of the dispersion curves for
![]() $z_{\text{m}}>z_{\text{A}}>z_{0}$
are shown in figure 9 for
$z_{\text{m}}>z_{\text{A}}>z_{0}$
are shown in figure 9 for
![]() $\unicode[STIX]{x1D70C}=0.1$
and
$\unicode[STIX]{x1D70C}=0.1$
and
![]() $\unicode[STIX]{x1D70C}=0.01$
. For
$\unicode[STIX]{x1D70C}=0.01$
. For
![]() $\unicode[STIX]{x1D703}=0$
, the solid curve corresponds to the L mode, and the solid vertical line corresponds to the A mode at
$\unicode[STIX]{x1D703}=0$
, the solid curve corresponds to the L mode, and the solid vertical line corresponds to the A mode at
![]() $z=z_{\text{A}}$
. The maximum in the solid curve is at
$z=z_{\text{A}}$
. The maximum in the solid curve is at
![]() $z=z_{\text{m}}$
, to the left of
$z=z_{\text{m}}$
, to the left of
![]() $z=z_{\text{A}}$
. This peak leads to a maximum and a minimum in the O mode dispersion curve for small
$z=z_{\text{A}}$
. This peak leads to a maximum and a minimum in the O mode dispersion curve for small
![]() $\unicode[STIX]{x1D703}$
. The maximum and minimum become smoothed out with increasing
$\unicode[STIX]{x1D703}$
. The maximum and minimum become smoothed out with increasing
![]() $\unicode[STIX]{x1D703}$
, and the dispersion curves are then qualitatively similar to those for
$\unicode[STIX]{x1D703}$
, and the dispersion curves are then qualitatively similar to those for
![]() $z_{\text{A}}>z_{\text{m}}$
when
$z_{\text{A}}>z_{\text{m}}$
when
![]() $z_{\text{A}}^{2}+b\tan ^{2}\unicode[STIX]{x1D703}>z_{\text{m}}^{2}$
. As
$z_{\text{A}}^{2}+b\tan ^{2}\unicode[STIX]{x1D703}>z_{\text{m}}^{2}$
. As
![]() $\unicode[STIX]{x1D703}$
increases the Alfvén mode moves downward, with asymptotes at
$\unicode[STIX]{x1D703}$
increases the Alfvén mode moves downward, with asymptotes at
![]() $z=z_{\text{A}}$
and
$z=z_{\text{A}}$
and
![]() $z=z_{0}$
remaining fixed. Only the branch with
$z=z_{0}$
remaining fixed. Only the branch with
![]() $z\approx z_{\text{A}}$
is Alfvén like, and we refer to the branch that links the asymptotic forms as the turnover branch. Landau damping becomes important in the range
$z\approx z_{\text{A}}$
is Alfvén like, and we refer to the branch that links the asymptotic forms as the turnover branch. Landau damping becomes important in the range
![]() $z_{\text{m}}>z>z_{0}$
, and this damping needs to be taken into account in a more detailed discussion of this case.
$z_{\text{m}}>z>z_{0}$
, and this damping needs to be taken into account in a more detailed discussion of this case.
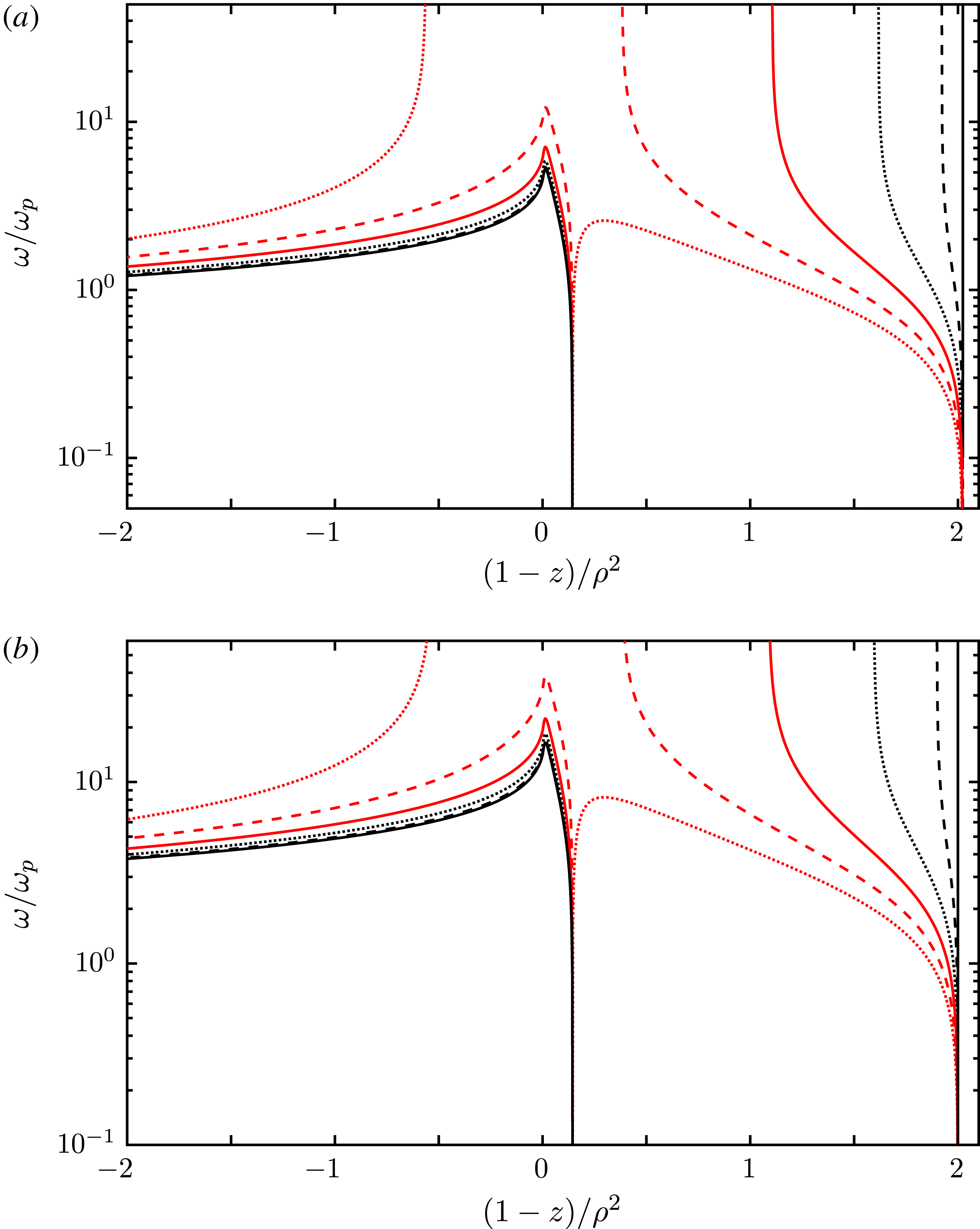
Figure 10. Similar to figure 8 but for
![]() $z_{\text{A}}<z_{0}$
and as a function of angle in steps of
$z_{\text{A}}<z_{0}$
and as a function of angle in steps of
![]() $0.45\unicode[STIX]{x1D70C}$
rad: (a)
$0.45\unicode[STIX]{x1D70C}$
rad: (a)
![]() $\unicode[STIX]{x1D70C}=0.1$
with
$\unicode[STIX]{x1D70C}=0.1$
with
![]() $\unicode[STIX]{x1D6FD}_{\text{A}}\approx 7.1$
and
$\unicode[STIX]{x1D6FD}_{\text{A}}\approx 7.1$
and
![]() $\unicode[STIX]{x1D6FE}_{\text{A}}\approx 5$
, (b)
$\unicode[STIX]{x1D6FE}_{\text{A}}\approx 5$
, (b)
![]() $\unicode[STIX]{x1D70C}=0.01$
with
$\unicode[STIX]{x1D70C}=0.01$
with
![]() $\unicode[STIX]{x1D6FD}_{\text{A}}\approx 71$
and
$\unicode[STIX]{x1D6FD}_{\text{A}}\approx 71$
and
![]() $\unicode[STIX]{x1D6FE}_{\text{A}}\approx 50$
.
$\unicode[STIX]{x1D6FE}_{\text{A}}\approx 50$
.
5.4.2 Case
 $z_{\text{A}}<z_{0}$
$z_{\text{A}}<z_{0}$
Examples of the dispersion curves for
![]() $z_{\text{A}}<z_{0}$
are shown in figure 10 for
$z_{\text{A}}<z_{0}$
are shown in figure 10 for
![]() $\unicode[STIX]{x1D70C}=0.1$
and
$\unicode[STIX]{x1D70C}=0.1$
and
![]() $\unicode[STIX]{x1D70C}=0.01$
. For parallel propagation the two dispersion curves do not cross. Equations (4.5) continue to apply, with
$\unicode[STIX]{x1D70C}=0.01$
. For parallel propagation the two dispersion curves do not cross. Equations (4.5) continue to apply, with
![]() $\unicode[STIX]{x1D714}_{\text{L}}^{2}(z)<0$
. As
$\unicode[STIX]{x1D714}_{\text{L}}^{2}(z)<0$
. As
![]() $\unicode[STIX]{x1D703}$
increases the L mode curve, including the peak, moves upward and to the left. The A mode dispersion curve moves to the left. The two curves meet at
$\unicode[STIX]{x1D703}$
increases the L mode curve, including the peak, moves upward and to the left. The A mode dispersion curve moves to the left. The two curves meet at
![]() $\unicode[STIX]{x1D714}=\infty$
at the angle determined by
$\unicode[STIX]{x1D714}=\infty$
at the angle determined by
![]() $z_{0}^{2}=z_{\text{A}}^{2}+b\tan ^{2}\unicode[STIX]{x1D703}$
. Further increase in
$z_{0}^{2}=z_{\text{A}}^{2}+b\tan ^{2}\unicode[STIX]{x1D703}$
. Further increase in
![]() $\unicode[STIX]{x1D703}$
leads to the O mode curve continuing to move upward and to the left, with the Alfvén mode curve moving downward, between asymptotes at
$\unicode[STIX]{x1D703}$
leads to the O mode curve continuing to move upward and to the left, with the Alfvén mode curve moving downward, between asymptotes at
![]() $z=z_{0}$
and
$z=z_{0}$
and
![]() $z=z_{\text{A}}$
.
$z=z_{\text{A}}$
.
It is questionable whether the reconnected mode in this case should be referred to as the Alfvén mode. It may also be regarded as an intrinsically new mode (Melrose & Gedalin Reference Melrose and Gedalin1999). The argument for this is as follows. The dispersion equation for oblique propagation in the form (4.5) gives
![]() $\unicode[STIX]{x1D714}^{2}$
in terms of three factors,
$\unicode[STIX]{x1D714}^{2}$
in terms of three factors,
![]() $z^{2}W(z)$
,
$z^{2}W(z)$
,
![]() $z^{2}-z_{\text{A}}^{2}$
and
$z^{2}-z_{\text{A}}^{2}$
and
![]() $z^{2}-z_{\text{A}}^{2}-b\tan ^{2}\unicode[STIX]{x1D703}$
. Real
$z^{2}-z_{\text{A}}^{2}-b\tan ^{2}\unicode[STIX]{x1D703}$
. Real
![]() $\unicode[STIX]{x1D714}^{2}$
requires that either all three factors are positive or that one is positive and two are negative. For
$\unicode[STIX]{x1D714}^{2}$
requires that either all three factors are positive or that one is positive and two are negative. For
![]() $z>z_{0}$
, the O mode corresponds to
$z>z_{0}$
, the O mode corresponds to
![]() $z^{2}W(z)>0$
and
$z^{2}W(z)>0$
and
![]() $z^{2}>z_{\text{A}}^{2}+b\tan ^{2}\unicode[STIX]{x1D703}>z_{\text{A}}^{2}$
and the Alfvén mode corresponds to
$z^{2}>z_{\text{A}}^{2}+b\tan ^{2}\unicode[STIX]{x1D703}>z_{\text{A}}^{2}$
and the Alfvén mode corresponds to
![]() $z^{2}W(z)>0$
and
$z^{2}W(z)>0$
and
![]() $z^{2}<z_{\text{A}}^{2}<z_{\text{A}}^{2}+b\tan ^{2}\unicode[STIX]{x1D703}$
. For
$z^{2}<z_{\text{A}}^{2}<z_{\text{A}}^{2}+b\tan ^{2}\unicode[STIX]{x1D703}$
. For
![]() $z<z_{0}$
, with
$z<z_{0}$
, with
![]() $z^{2}W(z)<0$
implying
$z^{2}W(z)<0$
implying
![]() $\unicode[STIX]{x1D714}_{\text{L}}^{2}(z)<0$
, this additional mode exists in the range
$\unicode[STIX]{x1D714}_{\text{L}}^{2}(z)<0$
, this additional mode exists in the range
![]() $z_{0}<z<z_{\text{A}}$
but only for sufficiently oblique propagation, specifically, for
$z_{0}<z<z_{\text{A}}$
but only for sufficiently oblique propagation, specifically, for
![]() $b\tan ^{2}\unicode[STIX]{x1D703}>z_{0}^{2}-z_{\text{A}}^{2}$
.
$b\tan ^{2}\unicode[STIX]{x1D703}>z_{0}^{2}-z_{\text{A}}^{2}$
.
6 Properties of resonant L mode waves
The wave properties of the (parallel) L mode in a pulsar plasma are of particular interest when considering beam-driven instabilities. The L mode is the nearest counterpart to the Langmuir mode in a non-relativistic plasma, but its properties have major differences from those of Langmuir waves. In this section we discuss some of these properties.
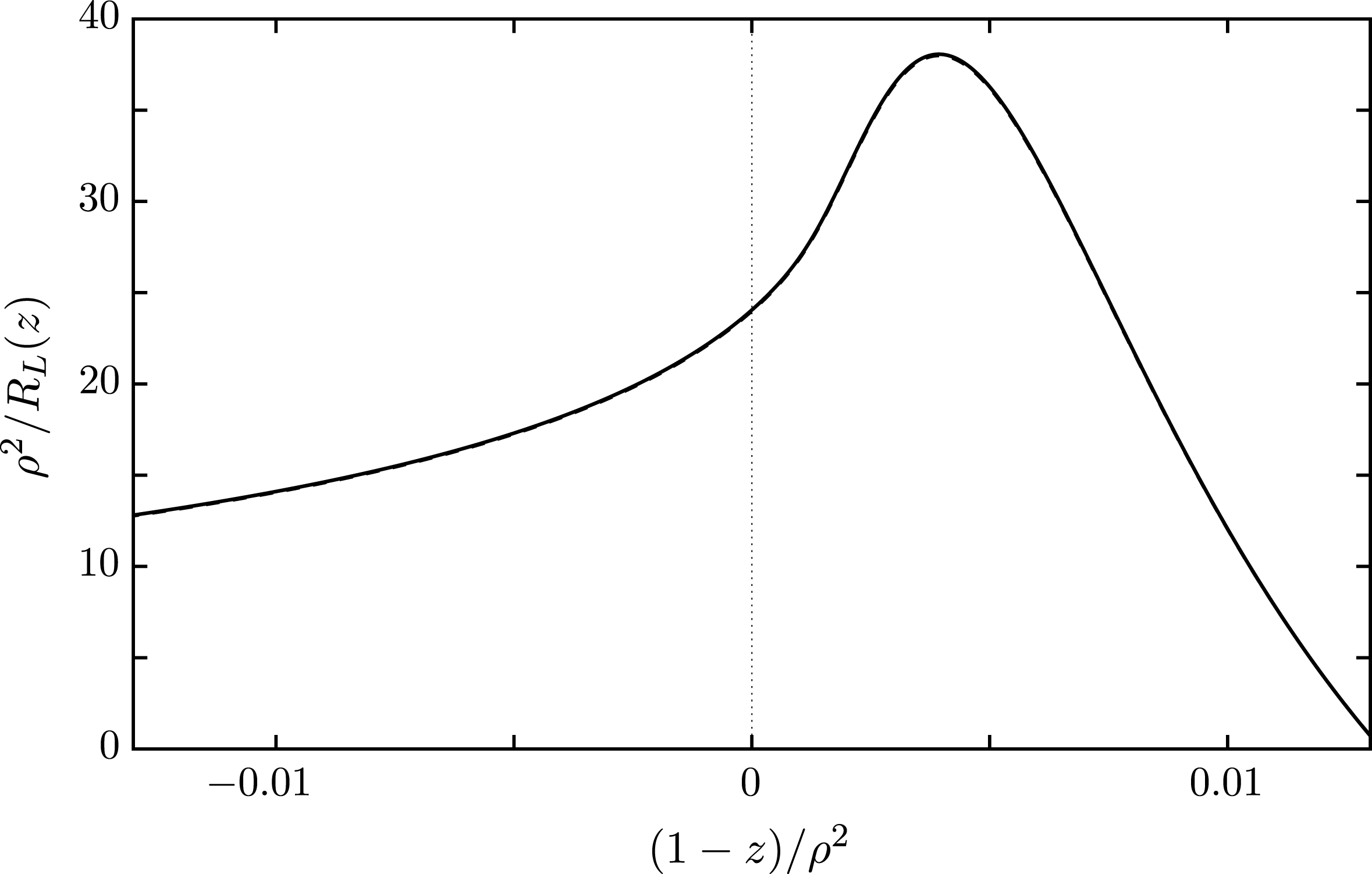
Figure 11. The function
![]() $\unicode[STIX]{x1D70C}^{2}/R_{\text{L}}(z)$
is plotted over
$\unicode[STIX]{x1D70C}^{2}/R_{\text{L}}(z)$
is plotted over
![]() $(1-z)/\unicode[STIX]{x1D70C}^{2}$
for
$(1-z)/\unicode[STIX]{x1D70C}^{2}$
for
![]() $\unicode[STIX]{x1D70C}=0.1$
(solid) and 0.01 (dashed). The two curves are indistinguishable over the scale shown. The thin dotted vertical line indicates the light line.
$\unicode[STIX]{x1D70C}=0.1$
(solid) and 0.01 (dashed). The two curves are indistinguishable over the scale shown. The thin dotted vertical line indicates the light line.
6.1 Ratio of electrical to total energy
In general the energy in waves in a specific mode in a dispersive medium may be separated into electric, magnetic and kinetic contributions, with the kinetic contribution attributed to the perturbations in the motion of particles forced by the wave (e.g. Melrose & McPhedran Reference Melrose and McPhedran1991, chap. 15). The total energy, which is the sum of the three, is determined by the dispersion theory, allowing one to infer the kinetic energy contribution. The magnetic energy is zero in a longitudinal wave. The ratio of the electric to total energy, denoted as
![]() $R_{\text{L}}(z)$
for the L mode, is relevant because the rate at which work is done by any source term involves only the electric energy, but the energy that appears in waves is the total energy.
$R_{\text{L}}(z)$
for the L mode, is relevant because the rate at which work is done by any source term involves only the electric energy, but the energy that appears in waves is the total energy.
The ratio
![]() $R_{\text{L}}(z)$
is evaluated in terms of
$R_{\text{L}}(z)$
is evaluated in terms of
![]() $W(z)$
in appendix C. Using the form (A 8) for the RPDF, this gives
$W(z)$
in appendix C. Using the form (A 8) for the RPDF, this gives
which is strictly valid only for superluminal waves,
![]() $z\geqslant 1$
. For
$z\geqslant 1$
. For
![]() $z\gg 1$
and
$z\gg 1$
and
![]() $z\rightarrow 1$
(6.1) gives
$z\rightarrow 1$
(6.1) gives
respectively, where the final approximation applies for a Jüttner distribution,
![]() $\langle \unicode[STIX]{x1D6FE}^{n}\rangle =n!\langle \unicode[STIX]{x1D6FE}\rangle ^{n}$
for
$\langle \unicode[STIX]{x1D6FE}^{n}\rangle =n!\langle \unicode[STIX]{x1D6FE}\rangle ^{n}$
for
![]() $\langle \unicode[STIX]{x1D6FE}\rangle \gg 1$
. One finds that
$\langle \unicode[STIX]{x1D6FE}\rangle \gg 1$
. One finds that
![]() $R_{\text{L}}(z)$
decreases with decreasing
$R_{\text{L}}(z)$
decreases with decreasing
![]() $z$
, from
$z$
, from
![]() $1/2$
in the limit
$1/2$
in the limit
![]() $z\rightarrow \infty$
, to
$z\rightarrow \infty$
, to
![]() $1/24\langle \unicode[STIX]{x1D6FE}\rangle ^{2}$
at
$1/24\langle \unicode[STIX]{x1D6FE}\rangle ^{2}$
at
![]() $z=1$
. For
$z=1$
. For
![]() $z$
in the range
$z$
in the range
![]() $1\gtrsim z\geqslant z_{\text{m}}\approx 1-0.13\unicode[STIX]{x1D70C}^{2}$
it is convenient to plot the inverse,
$1\gtrsim z\geqslant z_{\text{m}}\approx 1-0.13\unicode[STIX]{x1D70C}^{2}$
it is convenient to plot the inverse,
![]() $1/R_{\text{L}}(z)$
, rather than
$1/R_{\text{L}}(z)$
, rather than
![]() $R_{\text{L}}(z)$
itself, as illustrated in figure 11. The form of
$R_{\text{L}}(z)$
itself, as illustrated in figure 11. The form of
![]() $1/R_{\text{L}}(z)\propto 1/\unicode[STIX]{x1D70C}^{2}\approx \langle \unicode[STIX]{x1D6FE}\rangle ^{2}$
scales with
$1/R_{\text{L}}(z)\propto 1/\unicode[STIX]{x1D70C}^{2}\approx \langle \unicode[STIX]{x1D6FE}\rangle ^{2}$
scales with
![]() $(1-z)/\unicode[STIX]{x1D70C}^{2}$
, increasing with decreasing
$(1-z)/\unicode[STIX]{x1D70C}^{2}$
, increasing with decreasing
![]() $z$
through its value
$z$
through its value
![]() ${\approx}24\langle \unicode[STIX]{x1D6FE}\rangle ^{2}$
at
${\approx}24\langle \unicode[STIX]{x1D6FE}\rangle ^{2}$
at
![]() $z=1$
to a maximum
$z=1$
to a maximum
![]() ${\approx}38\langle \unicode[STIX]{x1D6FE}\rangle ^{2}$
at
${\approx}38\langle \unicode[STIX]{x1D6FE}\rangle ^{2}$
at
![]() $z\approx 1-0.004\unicode[STIX]{x1D70C}^{2}$
, and then decreasing with decreasing
$z\approx 1-0.004\unicode[STIX]{x1D70C}^{2}$
, and then decreasing with decreasing
![]() $z$
, passing through zero at
$z$
, passing through zero at
![]() $z=z_{\text{m}}$
and becoming negative in the region
$z=z_{\text{m}}$
and becoming negative in the region
![]() $z<z_{\text{m}}$
; as already remarked, we do not consider solutions in the region
$z<z_{\text{m}}$
; as already remarked, we do not consider solutions in the region
![]() $z<z_{\text{m}}$
where Landau damping is strong.
$z<z_{\text{m}}$
where Landau damping is strong.
6.2 Group speed
The velocity of energy propagation of waves in a dispersive medium may be identified as the ratio of the energy flux to the energy density, which is the group velocity, written here as
![]() $\unicode[STIX]{x1D6FD}_{\text{g}}c$
. It is shown in appendix C that
$\unicode[STIX]{x1D6FD}_{\text{g}}c$
. It is shown in appendix C that
![]() $\unicode[STIX]{x1D6FD}_{\text{g}}$
for the L mode is given by
$\unicode[STIX]{x1D6FD}_{\text{g}}$
for the L mode is given by
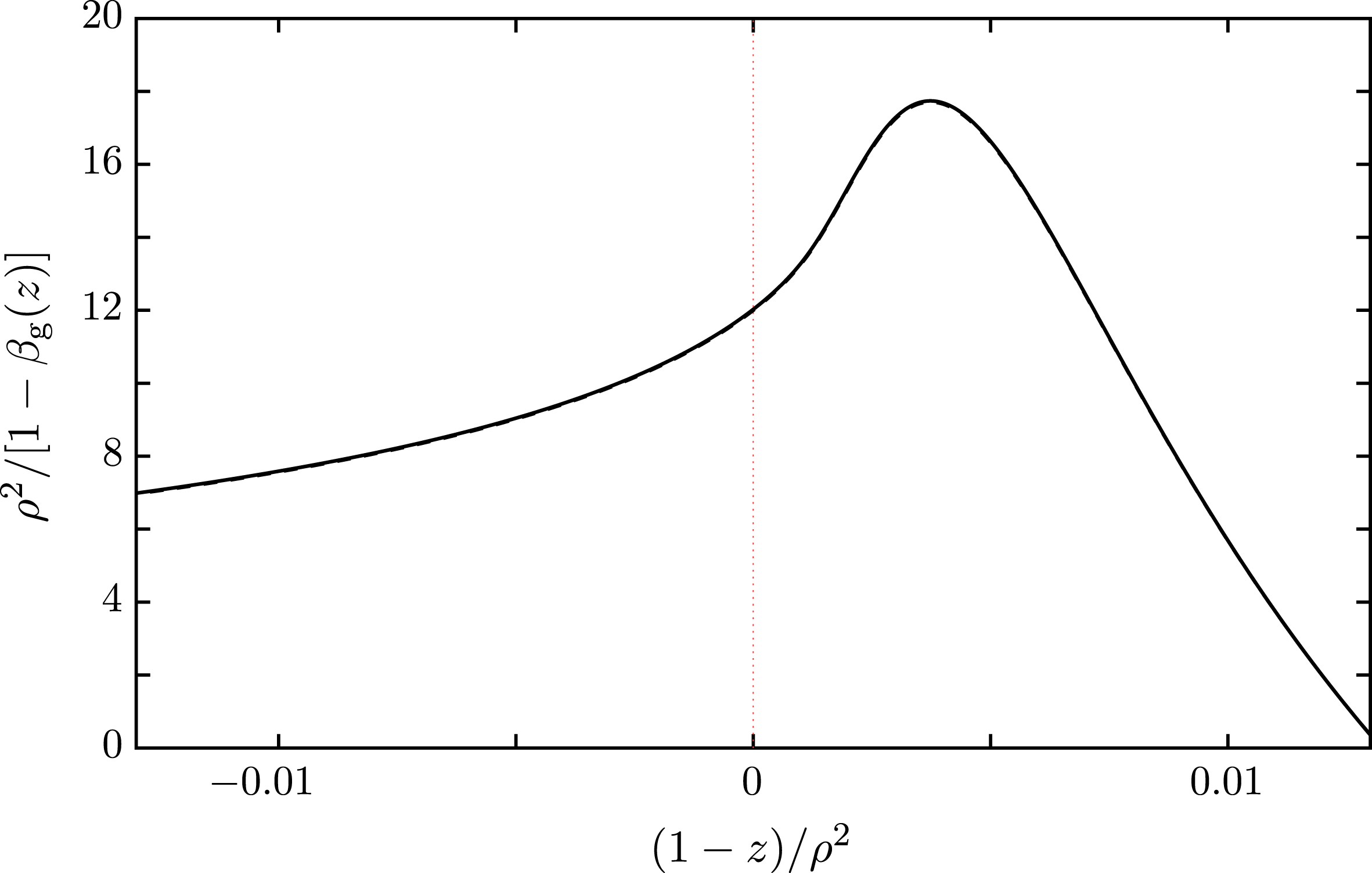
Figure 12. The function
![]() $\unicode[STIX]{x1D70C}^{2}/[1-\unicode[STIX]{x1D6FD}_{\text{g}}(z)]$
is plotted over
$\unicode[STIX]{x1D70C}^{2}/[1-\unicode[STIX]{x1D6FD}_{\text{g}}(z)]$
is plotted over
![]() $(1-z)/\unicode[STIX]{x1D70C}^{2}$
for
$(1-z)/\unicode[STIX]{x1D70C}^{2}$
for
![]() $\unicode[STIX]{x1D70C}=0.1$
(solid) and 0.01 (dashed). The two curves are indistinguishable over the scale shown. The thin dotted vertical line indicates the light line.
$\unicode[STIX]{x1D70C}=0.1$
(solid) and 0.01 (dashed). The two curves are indistinguishable over the scale shown. The thin dotted vertical line indicates the light line.
Approximations for
![]() $z\gg 1$
and
$z\gg 1$
and
![]() $z=1$
are
$z=1$
are
respectively. Thus, the group speed is zero at the cutoff frequency
![]() $\unicode[STIX]{x1D714}_{x}$
(where
$\unicode[STIX]{x1D714}_{x}$
(where
![]() $z\rightarrow \infty$
), and it increases with decreasing
$z\rightarrow \infty$
), and it increases with decreasing
![]() $z>1$
, approaching unity, but remaining subluminal (
$z>1$
, approaching unity, but remaining subluminal (
![]() $\unicode[STIX]{x1D6FD}_{\text{g}}<1$
) for
$\unicode[STIX]{x1D6FD}_{\text{g}}<1$
) for
![]() $z\rightarrow 1$
. For
$z\rightarrow 1$
. For
![]() $1>z\gg z_{\text{m}}$
the final expression in (6.3), and the form of
$1>z\gg z_{\text{m}}$
the final expression in (6.3), and the form of
![]() $R_{\text{L}}(z)$
shown in figure 11, imply that
$R_{\text{L}}(z)$
shown in figure 11, imply that
![]() $\unicode[STIX]{x1D6FD}_{\text{g}}$
gets closer to unity with decreasing
$\unicode[STIX]{x1D6FD}_{\text{g}}$
gets closer to unity with decreasing
![]() $z$
, reaching its maximum value at the maximum of
$z$
, reaching its maximum value at the maximum of
![]() $R_{\text{L}}(z)$
; it then decreases to zero at
$R_{\text{L}}(z)$
; it then decreases to zero at
![]() $z=z_{\text{m}}$
, as shown in figure 12. It follows from the scaling in the figure that
$z=z_{\text{m}}$
, as shown in figure 12. It follows from the scaling in the figure that
![]() $(1-\unicode[STIX]{x1D6FD}_{\text{g}})/(1-z)$
is approximately independent of
$(1-\unicode[STIX]{x1D6FD}_{\text{g}})/(1-z)$
is approximately independent of
![]() $\unicode[STIX]{x1D70C}$
for
$\unicode[STIX]{x1D70C}$
for
![]() $\unicode[STIX]{x1D70C}\ll 1$
.
$\unicode[STIX]{x1D70C}\ll 1$
.
We do not discuss the region
![]() $z<z_{\text{m}}$
in detail, but remark that (6.3) has properties that preclude the interpretation of
$z<z_{\text{m}}$
in detail, but remark that (6.3) has properties that preclude the interpretation of
![]() $\unicode[STIX]{x1D6FD}_{\text{g}}$
as the speed of (wave) energy propagation for
$\unicode[STIX]{x1D6FD}_{\text{g}}$
as the speed of (wave) energy propagation for
![]() $z<z_{\text{m}}$
: it becomes negative for
$z<z_{\text{m}}$
: it becomes negative for
![]() $z<z_{\text{m}}$
, singular at the zero of
$z<z_{\text{m}}$
, singular at the zero of
![]() $\text{d}W(z)/\text{d}z$
, where it changes sign to very large (superluminal group speed) and positive for smaller
$\text{d}W(z)/\text{d}z$
, where it changes sign to very large (superluminal group speed) and positive for smaller
![]() $z$
.
$z$
.
6.3 Wave properties for
 $1\geqslant z\gg z_{\text{m}}$
$1\geqslant z\gg z_{\text{m}}$
The only waves that can satisfy the resonance condition for a beam-driven instability in a pulsar plasma have properties that are quite different from those of Langmuir waves that can be beam driven in a non-relativistic plasma. Here we comment briefly on three unusual properties of the parallel-propagating waves in the L mode: the dispersion relation, the ratio of electric to total energy and the group speed.
In is convenient to write the condition
![]() $z=\unicode[STIX]{x1D6FD}_{\text{b}}$
for resonance with a beam with speed
$z=\unicode[STIX]{x1D6FD}_{\text{b}}$
for resonance with a beam with speed
![]() $\unicode[STIX]{x1D6FD}_{\text{b}}$
in terms of the corresponding Lorentz factor
$\unicode[STIX]{x1D6FD}_{\text{b}}$
in terms of the corresponding Lorentz factor
![]() $\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D719}}=\unicode[STIX]{x1D6FE}_{\text{b}}$
. For beam-driven growth to overcome Landau damping in the background plasma requires
$\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D719}}=\unicode[STIX]{x1D6FE}_{\text{b}}$
. For beam-driven growth to overcome Landau damping in the background plasma requires
![]() $\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D719}}\gg \unicode[STIX]{x1D6FE}_{\text{m}}$
, with
$\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D719}}\gg \unicode[STIX]{x1D6FE}_{\text{m}}$
, with
![]() $\unicode[STIX]{x1D6FE}_{\text{m}}\approx 6\langle \unicode[STIX]{x1D6FE}\rangle$
for
$\unicode[STIX]{x1D6FE}_{\text{m}}\approx 6\langle \unicode[STIX]{x1D6FE}\rangle$
for
![]() $\unicode[STIX]{x1D70C}\lesssim 1$
. In the example shown in figure 8, this corresponds to a tiny range of the solid black dispersion curve: to the right of
$\unicode[STIX]{x1D70C}\lesssim 1$
. In the example shown in figure 8, this corresponds to a tiny range of the solid black dispersion curve: to the right of
![]() $(1-z)/\unicode[STIX]{x1D70C}^{2}=0$
and to the left of the peak in the curve at
$(1-z)/\unicode[STIX]{x1D70C}^{2}=0$
and to the left of the peak in the curve at
![]() $z=z_{\text{m}}$
. Over this range
$z=z_{\text{m}}$
. Over this range
![]() $\unicode[STIX]{x1D714}_{\text{L}}(z)$
is a rapidly decreasing function of
$\unicode[STIX]{x1D714}_{\text{L}}(z)$
is a rapidly decreasing function of
![]() $z$
, with
$z$
, with
where the approximation applies for
![]() $\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D719}}\gg \unicode[STIX]{x1D6FE}_{\text{m}}$
. With
$\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D719}}\gg \unicode[STIX]{x1D6FE}_{\text{m}}$
. With
![]() $1/2R_{\text{L}}(z)$
ranging between
$1/2R_{\text{L}}(z)$
ranging between
![]() $12\langle \unicode[STIX]{x1D6FE}\rangle ^{2}$
and
$12\langle \unicode[STIX]{x1D6FE}\rangle ^{2}$
and
![]() $19\langle \unicode[STIX]{x1D6FE}\rangle ^{2}$
for
$19\langle \unicode[STIX]{x1D6FE}\rangle ^{2}$
for
![]() $z<1$
, cf. figure 11, it follows that the frequency
$z<1$
, cf. figure 11, it follows that the frequency
![]() $\unicode[STIX]{x1D714}_{\text{L}}(z)$
is a very strong function of
$\unicode[STIX]{x1D714}_{\text{L}}(z)$
is a very strong function of
![]() $z$
over the tiny range of
$z$
over the tiny range of
![]() $z$
where resonant wave growth is possible. This is quite different from Langmuir waves, for which the frequency is only a weak function over a wide range of phase speeds. It is also quite different from ion (or electron) acoustic waves, for which the phase speed is approximately equal to the ion (or electron) sound speed.
$z$
where resonant wave growth is possible. This is quite different from Langmuir waves, for which the frequency is only a weak function over a wide range of phase speeds. It is also quite different from ion (or electron) acoustic waves, for which the phase speed is approximately equal to the ion (or electron) sound speed.
A second feature that is not ‘Langmuir like’ is that the ratio of electric to total energy
![]() $R_{\text{L}}(z)$
is very small for L mode waves in the range
$R_{\text{L}}(z)$
is very small for L mode waves in the range
![]() $1>z\gg z_{\text{m}}$
. In contrast, for Langmuir waves the ratio is approximately
$1>z\gg z_{\text{m}}$
. In contrast, for Langmuir waves the ratio is approximately
![]() $1/2$
, corresponding to approximate equipartition between electric energy and kinetic energy of forced motions in the wave. The very small value of
$1/2$
, corresponding to approximate equipartition between electric energy and kinetic energy of forced motions in the wave. The very small value of
![]() $R_{\text{L}}(z)$
is unusual when compared with Langmuir waves, but not when compared with ion acoustic waves, which have
$R_{\text{L}}(z)$
is unusual when compared with Langmuir waves, but not when compared with ion acoustic waves, which have
![]() $R_{\text{L}}\approx k^{2}\unicode[STIX]{x1D706}_{\text{De}}^{2}\ll 1$
, where
$R_{\text{L}}\approx k^{2}\unicode[STIX]{x1D706}_{\text{De}}^{2}\ll 1$
, where
![]() $k$
is the wavenumber and
$k$
is the wavenumber and
![]() $\unicode[STIX]{x1D706}_{\text{De}}$
is the electron Debye length.
$\unicode[STIX]{x1D706}_{\text{De}}$
is the electron Debye length.
The group speed for L waves is only marginally subluminal,
![]() $1-\unicode[STIX]{x1D6FD}_{\text{g}}(z)\ll 1$
, in the relevant range,
$1-\unicode[STIX]{x1D6FD}_{\text{g}}(z)\ll 1$
, in the relevant range,
![]() $1>z\gg z_{\text{m}}$
. The small group speed for Langmuir waves implies that the wave energy that grows in a given region due to a beam-driven instability remains localized to that region as the beam propagates through it. However,
$1>z\gg z_{\text{m}}$
. The small group speed for Langmuir waves implies that the wave energy that grows in a given region due to a beam-driven instability remains localized to that region as the beam propagates through it. However,
![]() $\unicode[STIX]{x1D6FD}_{\text{g}}(z)\approx 1$
for the relevant L mode waves implies that the wave energy propagates away at nearly the speed of light, impeding any wave growth.
$\unicode[STIX]{x1D6FD}_{\text{g}}(z)\approx 1$
for the relevant L mode waves implies that the wave energy propagates away at nearly the speed of light, impeding any wave growth.
7 Discussion and conclusions
We discuss wave dispersion in a pulsar plasma, defined as a strongly magnetized pair plasma with a 1-D Jüttner distribution. We find that the relativistic plasma dispersion function (RPDF) scales in a characteristic way with inverse temperature in the highly relativistic case,
![]() $\unicode[STIX]{x1D70C}\ll 1$
. The favoured case
$\unicode[STIX]{x1D70C}\ll 1$
. The favoured case
![]() $\unicode[STIX]{x1D70C}\approx 1$
is more closely analogous to the highly relativistic case than to the non-relativistic case,
$\unicode[STIX]{x1D70C}\approx 1$
is more closely analogous to the highly relativistic case than to the non-relativistic case,
![]() $\unicode[STIX]{x1D70C}\gg 1$
.
$\unicode[STIX]{x1D70C}\gg 1$
.
Wave dispersion in the rest frame of a pulsar plasma is strongly modified compared with wave dispersion in more familiar non-relativistic plasmas. One difference is due to the Alfvén speed,
![]() $\unicode[STIX]{x1D6FD}_{\text{A}}c$
, being highly relativistic
$\unicode[STIX]{x1D6FD}_{\text{A}}c$
, being highly relativistic
![]() $\unicode[STIX]{x1D6FD}_{\text{A}}\gg 1$
. It is well known that the displacement current then plays an important role, and that the phase speed of Alfvén and magnetoacoustic waves (in a cold plasma) is determined by
$\unicode[STIX]{x1D6FD}_{\text{A}}\gg 1$
. It is well known that the displacement current then plays an important role, and that the phase speed of Alfvén and magnetoacoustic waves (in a cold plasma) is determined by
![]() $\unicode[STIX]{x1D6FD}_{0}=\unicode[STIX]{x1D6FD}_{\text{A}}/(1+\unicode[STIX]{x1D6FD}_{\text{A}}^{2})^{1/2}<1$
rather than
$\unicode[STIX]{x1D6FD}_{0}=\unicode[STIX]{x1D6FD}_{\text{A}}/(1+\unicode[STIX]{x1D6FD}_{\text{A}}^{2})^{1/2}<1$
rather than
![]() $\unicode[STIX]{x1D6FD}_{\text{A}}$
. The parameter
$\unicode[STIX]{x1D6FD}_{\text{A}}$
. The parameter
![]() $z_{\text{A}}$
used here is approximately equal to
$z_{\text{A}}$
used here is approximately equal to
![]() $\unicode[STIX]{x1D6FD}_{0}$
in a highly relativistic plasma, cf. (A 11). Another difference is that the relativistic plasma dispersion function (RPDF) becomes extremely sharply peaked, compared with its non-relativistic counterpart, and this has a large effect on some aspects of the wave dispersion. A third difference concerns the cross-over between the dispersion curves for the L and A mode. A cross-over necessarily occurs in the cold-plasma case, and it leads to a resonance (
$\unicode[STIX]{x1D6FD}_{0}$
in a highly relativistic plasma, cf. (A 11). Another difference is that the relativistic plasma dispersion function (RPDF) becomes extremely sharply peaked, compared with its non-relativistic counterpart, and this has a large effect on some aspects of the wave dispersion. A third difference concerns the cross-over between the dispersion curves for the L and A mode. A cross-over necessarily occurs in the cold-plasma case, and it leads to a resonance (
![]() $N^{2}\rightarrow \infty$
,
$N^{2}\rightarrow \infty$
,
![]() $z\rightarrow 0$
) in the Alfvén mode. In the relativistic case, the cross-over occurs only for
$z\rightarrow 0$
) in the Alfvén mode. In the relativistic case, the cross-over occurs only for
![]() $z_{\text{A}}>z_{0}$
or
$z_{\text{A}}>z_{0}$
or
![]() $\unicode[STIX]{x1D6FD}_{\text{A}}>\unicode[STIX]{x1D6FE}_{0}\gg 1$
, which condition is satisfied for plausible pulsar parameters. Then there is a turnover, rather than a resonance, in the Alfvén mode. We note that for
$\unicode[STIX]{x1D6FD}_{\text{A}}>\unicode[STIX]{x1D6FE}_{0}\gg 1$
, which condition is satisfied for plausible pulsar parameters. Then there is a turnover, rather than a resonance, in the Alfvén mode. We note that for
![]() $z_{\text{A}}<z_{0}$
there is no cross-over for
$z_{\text{A}}<z_{0}$
there is no cross-over for
![]() $\unicode[STIX]{x1D703}=0$
; in this case the modes reconnection for
$\unicode[STIX]{x1D703}=0$
; in this case the modes reconnection for
![]() $b\tan ^{2}\unicode[STIX]{x1D703}=z_{0}^{2}-z_{\text{A}}^{2}$
, forming (the O mode and) an intrinsically oblique Alfvén-like mode (which we do not discuss in this paper).
$b\tan ^{2}\unicode[STIX]{x1D703}=z_{0}^{2}-z_{\text{A}}^{2}$
, forming (the O mode and) an intrinsically oblique Alfvén-like mode (which we do not discuss in this paper).
A motivation for the investigation reported here was an argument that beam-driven RPE is the most plausible emission mechanism for the nanoshots from the Crab pulsar (Eilek & Hankins Reference Eilek and Hankins2016). This suggestion is based on the assumption that the beam causes Langmuir-like waves to grow to a very high level in a localized region, with some nonlinear plasma process partly converting the wave energy into escaping radio emission (Weatherall Reference Weatherall1997, Reference Weatherall1998). It is implicit in this model that Langmuir-like waves exist in the plasma, and that they are relatively slowly propagating, such that their group speed is small compared with the beam speed. Similar assumptions were made in most early models of RPE, where Langmuir-like waves were simply assumed to exist. However, none of the wave modes discussed in the present paper satisfy all the requirements for ‘Langmuir-like’ waves implicit in these models, specifically waves that can grow due to resonance with a beam and that are slowly propagating compared with the beam. Such resonance requires
![]() $\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D719}}=\unicode[STIX]{x1D6FE}_{\text{b}}$
, where
$\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D719}}=\unicode[STIX]{x1D6FE}_{\text{b}}$
, where
![]() $\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D719}}$
and
$\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D719}}$
and
![]() $\unicode[STIX]{x1D6FE}_{\text{b}}$
are the Lorentz factors corresponding to the phase speed of the wave and the beam speed, respectively. The only relevant subluminal waves are the O mode at sufficiently small angles
$\unicode[STIX]{x1D6FE}_{\text{b}}$
are the Lorentz factors corresponding to the phase speed of the wave and the beam speed, respectively. The only relevant subluminal waves are the O mode at sufficiently small angles
![]() $\unicode[STIX]{x1D703}$
, which has
$\unicode[STIX]{x1D703}$
, which has
![]() $\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D719}}>\unicode[STIX]{x1D6FD}_{\text{A}}$
, and the Alfvén mode which has
$\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D719}}>\unicode[STIX]{x1D6FD}_{\text{A}}$
, and the Alfvén mode which has
![]() $\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D719}}\approx \unicode[STIX]{x1D6FD}_{\text{A}}$
at low frequencies and turns over at higher frequencies, where
$\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D719}}\approx \unicode[STIX]{x1D6FD}_{\text{A}}$
at low frequencies and turns over at higher frequencies, where
![]() $\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D719}}$
decreases from
$\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D719}}$
decreases from
![]() ${\approx}\unicode[STIX]{x1D6FD}_{\text{A}}$
to of the order of
${\approx}\unicode[STIX]{x1D6FD}_{\text{A}}$
to of the order of
![]() $\langle \unicode[STIX]{x1D6FE}\rangle$
, as shown in figure 8. The nearest approximation to a ‘Langmuir-like’ mode is the Alfvén mode near the turnover at
$\langle \unicode[STIX]{x1D6FE}\rangle$
, as shown in figure 8. The nearest approximation to a ‘Langmuir-like’ mode is the Alfvén mode near the turnover at
![]() $z=z_{\text{m}}$
, where its group speed is zero. Although beam-driven growth of Alfvén waves has been discussed as a possible pulsar emission mechanism (Tsytovich & Kaplan Reference Tsytovich and Kaplan1972; Lominadze et al.
Reference Lominadze, Stenflo, Tsytovich and Wilhelmsson1982; Melrose & Gedalin Reference Melrose and Gedalin1999; Lyutikov Reference Lyutikov2000), the role that this turnover might play has not been discussed.
$z=z_{\text{m}}$
, where its group speed is zero. Although beam-driven growth of Alfvén waves has been discussed as a possible pulsar emission mechanism (Tsytovich & Kaplan Reference Tsytovich and Kaplan1972; Lominadze et al.
Reference Lominadze, Stenflo, Tsytovich and Wilhelmsson1982; Melrose & Gedalin Reference Melrose and Gedalin1999; Lyutikov Reference Lyutikov2000), the role that this turnover might play has not been discussed.
A discussion of the implications of these results for pulsar radio emission requires detailed estimates of the plasma parameters, which we propose to give elsewhere. However, simple estimates suggest that RPE encounters serious difficulties. The conditions
![]() $\unicode[STIX]{x1D6FE}_{\text{b}}=\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D719}}$
and
$\unicode[STIX]{x1D6FE}_{\text{b}}=\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D719}}$
and
![]() $\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D719}}>\unicode[STIX]{x1D6FD}_{\text{A}}$
can be satisfied only for an extremely high-energy beam, due to
$\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D719}}>\unicode[STIX]{x1D6FD}_{\text{A}}$
can be satisfied only for an extremely high-energy beam, due to
![]() $\unicode[STIX]{x1D6FD}_{\text{A}}$
being extremely large in a pulsar magnetosphere. For example, consider an estimate of
$\unicode[STIX]{x1D6FD}_{\text{A}}$
being extremely large in a pulsar magnetosphere. For example, consider an estimate of
![]() $\unicode[STIX]{x1D6FD}_{\text{A}}^{2}=\unicode[STIX]{x1D6FA}_{\text{e}}^{2}/\unicode[STIX]{x1D714}_{\text{p}}^{2}\langle \unicode[STIX]{x1D6FE}\rangle$
with
$\unicode[STIX]{x1D6FD}_{\text{A}}^{2}=\unicode[STIX]{x1D6FA}_{\text{e}}^{2}/\unicode[STIX]{x1D714}_{\text{p}}^{2}\langle \unicode[STIX]{x1D6FE}\rangle$
with
![]() $\unicode[STIX]{x1D6FA}_{\text{e}}$
evaluated for a magnetic field
$\unicode[STIX]{x1D6FA}_{\text{e}}$
evaluated for a magnetic field
![]() $B=10^{8}$
T and the plasma frequency given by
$B=10^{8}$
T and the plasma frequency given by
![]() $\unicode[STIX]{x1D714}_{\text{p}}^{2}\approx \unicode[STIX]{x1D705}\unicode[STIX]{x1D6FA}_{\text{e}}\unicode[STIX]{x1D6FA}_{\ast }/\unicode[STIX]{x1D6FE}_{\text{s}}$
, with
$\unicode[STIX]{x1D714}_{\text{p}}^{2}\approx \unicode[STIX]{x1D705}\unicode[STIX]{x1D6FA}_{\text{e}}\unicode[STIX]{x1D6FA}_{\ast }/\unicode[STIX]{x1D6FE}_{\text{s}}$
, with
![]() $\unicode[STIX]{x1D705}$
the multiplicity (ratio of number density to the corotation charge density
$\unicode[STIX]{x1D705}$
the multiplicity (ratio of number density to the corotation charge density
![]() $/e$
),
$/e$
),
![]() $\unicode[STIX]{x1D6FA}_{\ast }=2\unicode[STIX]{x03C0}/P$
the rotation frequency of the star and
$\unicode[STIX]{x1D6FA}_{\ast }=2\unicode[STIX]{x03C0}/P$
the rotation frequency of the star and
![]() $\unicode[STIX]{x1D6FE}_{\text{s}}$
the Lorentz factor of the transformation between the rest frame and the pulsar frame. This gives
$\unicode[STIX]{x1D6FE}_{\text{s}}$
the Lorentz factor of the transformation between the rest frame and the pulsar frame. This gives
![]() $\unicode[STIX]{x1D6FD}_{\text{A}}^{2}$
of order
$\unicode[STIX]{x1D6FD}_{\text{A}}^{2}$
of order
![]() $10^{19}\unicode[STIX]{x1D6FD}_{\text{s}}P/\unicode[STIX]{x1D705}\langle \unicode[STIX]{x1D6FE}\rangle$
near the surface of the star. For values
$10^{19}\unicode[STIX]{x1D6FD}_{\text{s}}P/\unicode[STIX]{x1D705}\langle \unicode[STIX]{x1D6FE}\rangle$
near the surface of the star. For values
![]() $P=1$
s,
$P=1$
s,
![]() $\unicode[STIX]{x1D705}=10^{5}$
,
$\unicode[STIX]{x1D705}=10^{5}$
,
![]() $\unicode[STIX]{x1D6FE}_{\text{s}}=10^{3}$
,
$\unicode[STIX]{x1D6FE}_{\text{s}}=10^{3}$
,
![]() $\langle \unicode[STIX]{x1D6FE}\rangle =10$
this implies
$\langle \unicode[STIX]{x1D6FE}\rangle =10$
this implies
![]() $\unicode[STIX]{x1D6FD}_{\text{A}}^{2}$
of order
$\unicode[STIX]{x1D6FD}_{\text{A}}^{2}$
of order
![]() $10^{15}$
. For a dipolar magnetic field
$10^{15}$
. For a dipolar magnetic field
![]() $B\propto 1/r^{3}$
one has
$B\propto 1/r^{3}$
one has
![]() $\unicode[STIX]{x1D6FD}_{\text{A}}^{2}\propto 1/r^{3}$
, but
$\unicode[STIX]{x1D6FD}_{\text{A}}^{2}\propto 1/r^{3}$
, but
![]() $\unicode[STIX]{x1D6FD}_{\text{A}}$
remains very large, except perhaps near the light-cylinder radius,
$\unicode[STIX]{x1D6FD}_{\text{A}}$
remains very large, except perhaps near the light-cylinder radius,
![]() $r_{\text{L}}=Pc/2\unicode[STIX]{x03C0}$
. The most energetic beams considered plausible have Lorentz factors of order
$r_{\text{L}}=Pc/2\unicode[STIX]{x03C0}$
. The most energetic beams considered plausible have Lorentz factors of order
![]() $10^{6}$
–
$10^{6}$
–
![]() $10^{7}$
in the pulsar frame, and hence of order
$10^{7}$
in the pulsar frame, and hence of order
![]() $10^{3}$
–
$10^{3}$
–
![]() $10^{4}$
in the rest frame. We conclude that for the O mode, the resonance condition fails to be satisfied by many orders of magnitude for a source near the star. Moreover, O mode waves are not Langmuir like in that their group speed is not slow but is close to the speed of light, and as they propagate the angle
$10^{4}$
in the rest frame. We conclude that for the O mode, the resonance condition fails to be satisfied by many orders of magnitude for a source near the star. Moreover, O mode waves are not Langmuir like in that their group speed is not slow but is close to the speed of light, and as they propagate the angle
![]() $\unicode[STIX]{x1D703}$
increases due to the curvature of the field lines, so that
$\unicode[STIX]{x1D703}$
increases due to the curvature of the field lines, so that
![]() $\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D719}}$
increases and the waves quickly move out of resonance and become superluminal. We conclude that the assumption that the energy in these waves remains localized and builds up due to the beam propagating through the location is not justified.
$\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D719}}$
increases and the waves quickly move out of resonance and become superluminal. We conclude that the assumption that the energy in these waves remains localized and builds up due to the beam propagating through the location is not justified.
It is possible in principle for waves in the Alfvén mode to grow. However, for Alfvén waves at low frequencies, which satisfy the dispersion relation
![]() $z\approx z_{\text{A}}$
, the resonance condition is
$z\approx z_{\text{A}}$
, the resonance condition is
![]() $\unicode[STIX]{x1D6FE}_{\text{b}}\approx \unicode[STIX]{x1D6FD}_{\text{A}}$
and the foregoing discussion of the O mode also applies to such Alfvén waves: the resonance condition cannot be satisfied under plausible conditions anywhere in the pulsar magnetosphere. At higher frequencies, as shown in figure 8, the dispersion relation turns over, with the turnover frequency decreasing with increasing
$\unicode[STIX]{x1D6FE}_{\text{b}}\approx \unicode[STIX]{x1D6FD}_{\text{A}}$
and the foregoing discussion of the O mode also applies to such Alfvén waves: the resonance condition cannot be satisfied under plausible conditions anywhere in the pulsar magnetosphere. At higher frequencies, as shown in figure 8, the dispersion relation turns over, with the turnover frequency decreasing with increasing
![]() $\unicode[STIX]{x1D703}$
; with
$\unicode[STIX]{x1D703}$
; with
![]() $(1-z)/\unicode[STIX]{x1D70C}^{2}\approx \langle \unicode[STIX]{x1D6FE}\rangle ^{2}/2\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D719}}^{2}$
, the turnover occurs at
$(1-z)/\unicode[STIX]{x1D70C}^{2}\approx \langle \unicode[STIX]{x1D6FE}\rangle ^{2}/2\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D719}}^{2}$
, the turnover occurs at
![]() $\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D719}}\approx 6\,\langle \unicode[STIX]{x1D6FE}\rangle$
, and Landau damping becomes important at about this and smaller
$\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D719}}\approx 6\,\langle \unicode[STIX]{x1D6FE}\rangle$
, and Landau damping becomes important at about this and smaller
![]() $\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D719}}$
. It follows that near the turnover, a beam with
$\unicode[STIX]{x1D6FE}_{\unicode[STIX]{x1D719}}$
. It follows that near the turnover, a beam with
![]() $\unicode[STIX]{x1D6FE}_{\text{b}}\approx 6\,\langle \unicode[STIX]{x1D6FE}\rangle$
can cause Alfvén waves to grow. Moreover, the group speed is small near the turnover, where
$\unicode[STIX]{x1D6FE}_{\text{b}}\approx 6\,\langle \unicode[STIX]{x1D6FE}\rangle$
can cause Alfvén waves to grow. Moreover, the group speed is small near the turnover, where
![]() $\unicode[STIX]{x2202}\unicode[STIX]{x1D714}/\unicode[STIX]{x2202}z$
passes through zero, favouring energy in these waves building up rather than propagating away. The properties of Alfvén waves near the turnover frequency were not taken into account in earlier models for beam-driven growth of Alfvén waves in a pulsar plasma (Tsytovich & Kaplan Reference Tsytovich and Kaplan1972; Lominadze et al.
Reference Lominadze, Stenflo, Tsytovich and Wilhelmsson1982; Melrose & Gedalin Reference Melrose and Gedalin1999; Lyutikov Reference Lyutikov2000).
$\unicode[STIX]{x2202}\unicode[STIX]{x1D714}/\unicode[STIX]{x2202}z$
passes through zero, favouring energy in these waves building up rather than propagating away. The properties of Alfvén waves near the turnover frequency were not taken into account in earlier models for beam-driven growth of Alfvén waves in a pulsar plasma (Tsytovich & Kaplan Reference Tsytovich and Kaplan1972; Lominadze et al.
Reference Lominadze, Stenflo, Tsytovich and Wilhelmsson1982; Melrose & Gedalin Reference Melrose and Gedalin1999; Lyutikov Reference Lyutikov2000).
The discussion of the wave dispersion in this paper applies to waves in the rest frame of a pulsar plasma at frequencies well below the electron cyclotron frequency. Our choice of the rest frame of the plasma is convenient for formal purposes, but the relevant frame from an observational viewpoint is the pulsar frame, in which the pair plasma is streaming outward with Lorentz factor
![]() $\unicode[STIX]{x1D6FE}_{\text{s}}$
. In Part 2 we discuss the Lorentz transformation to the pulsar frame, and consider various aspects of the wave dispersion in that frame and in other frames where there are relative streaming motions between different distributions of particles.
$\unicode[STIX]{x1D6FE}_{\text{s}}$
. In Part 2 we discuss the Lorentz transformation to the pulsar frame, and consider various aspects of the wave dispersion in that frame and in other frames where there are relative streaming motions between different distributions of particles.
Acknowledgements
We thank M. Wheatland, referee V. S. Beskin and an anonymous referee for helpful comments on the manuscript. The research reported in this paper was supported by the Australian Research Council through grant DP160102932.
Appendix A. Dispersion equation
Here we present the derivation of non-zero components of
![]() $\unicode[STIX]{x1D6EC}_{ij}(\unicode[STIX]{x1D714},\boldsymbol{k})$
, defined in (A 10), and discuss our assumptions.
$\unicode[STIX]{x1D6EC}_{ij}(\unicode[STIX]{x1D714},\boldsymbol{k})$
, defined in (A 10), and discuss our assumptions.
A.1 Dielectric tensor
Consider a plasma that is composed of electrons,
![]() $\unicode[STIX]{x1D716}=-1$
, and positrons,
$\unicode[STIX]{x1D716}=-1$
, and positrons,
![]() $\unicode[STIX]{x1D716}=+1$
. The general form for the dielectric tensor derived using kinetic theory involves a sum over
$\unicode[STIX]{x1D716}=+1$
. The general form for the dielectric tensor derived using kinetic theory involves a sum over
![]() $\unicode[STIX]{x1D716}=\pm 1$
. For a 1-D distribution it is convenient to replace the conventional distribution function,
$\unicode[STIX]{x1D716}=\pm 1$
. For a 1-D distribution it is convenient to replace the conventional distribution function,
![]() $f_{\unicode[STIX]{x1D716}}(p_{\bot },p_{\Vert })$
, and the integral over
$f_{\unicode[STIX]{x1D716}}(p_{\bot },p_{\Vert })$
, and the integral over
![]() $2\unicode[STIX]{x03C0}\text{d}p_{\Vert }\text{d}p_{\bot }\,p_{\bot }$
by the 1-D distribution
$2\unicode[STIX]{x03C0}\text{d}p_{\Vert }\text{d}p_{\bot }\,p_{\bot }$
by the 1-D distribution
![]() $g_{\unicode[STIX]{x1D716}}(u)$
with
$g_{\unicode[STIX]{x1D716}}(u)$
with
![]() $p_{\bot }=0$
,
$p_{\bot }=0$
,
![]() $p_{\Vert }=mcu$
,
$p_{\Vert }=mcu$
,
![]() $u=\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FD}$
and the integral over
$u=\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FD}$
and the integral over
![]() $du$
. The dielectric tensor is given by (Melrose Reference Melrose2008, Reference Melrose2013)
$du$
. The dielectric tensor is given by (Melrose Reference Melrose2008, Reference Melrose2013)
with
![]() $\unicode[STIX]{x1D608}_{ij}(\unicode[STIX]{x1D714},\boldsymbol{k};\unicode[STIX]{x1D6FD})\rightarrow \unicode[STIX]{x1D608}_{ij}$
given by (A 4) below, and with plasma frequency
$\unicode[STIX]{x1D608}_{ij}(\unicode[STIX]{x1D714},\boldsymbol{k};\unicode[STIX]{x1D6FD})\rightarrow \unicode[STIX]{x1D608}_{ij}$
given by (A 4) below, and with plasma frequency
![]() $\unicode[STIX]{x1D714}_{p\unicode[STIX]{x1D716}}^{2}=e^{2}n_{\unicode[STIX]{x1D716}}/\unicode[STIX]{x1D700}_{0}m$
, where
$\unicode[STIX]{x1D714}_{p\unicode[STIX]{x1D716}}^{2}=e^{2}n_{\unicode[STIX]{x1D716}}/\unicode[STIX]{x1D700}_{0}m$
, where
![]() $n_{\unicode[STIX]{x1D716}}$
is the number density of electrons or positrons in the plasma rest frame. The average
$n_{\unicode[STIX]{x1D716}}$
is the number density of electrons or positrons in the plasma rest frame. The average
![]() $\langle Q\rangle$
of any function
$\langle Q\rangle$
of any function
![]() $Q$
of
$Q$
of
![]() $u$
is written as
$u$
is written as
which defines the number density,
![]() $n_{\unicode[STIX]{x1D716}}$
, for
$n_{\unicode[STIX]{x1D716}}$
, for
![]() $Q=1$
.
$Q=1$
.
With the magnetic field along the 3-axis and the wave vector in the 1–3 plane, we introduce the notation
The components of the tensor
![]() $\unicode[STIX]{x1D608}_{ij}$
in (A 1) are
$\unicode[STIX]{x1D608}_{ij}$
in (A 1) are
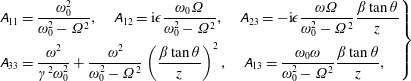 $$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}l@{}}\unicode[STIX]{x1D608}_{11}={\displaystyle \frac{\unicode[STIX]{x1D714}_{0}^{2}}{\unicode[STIX]{x1D714}_{0}^{2}-\unicode[STIX]{x1D6FA}^{2}}},\quad \unicode[STIX]{x1D608}_{12}=\text{i}\unicode[STIX]{x1D716}{\displaystyle \frac{\unicode[STIX]{x1D714}_{0}\unicode[STIX]{x1D6FA}}{\unicode[STIX]{x1D714}_{0}^{2}-\unicode[STIX]{x1D6FA}^{2}}},\quad \unicode[STIX]{x1D608}_{23}=-\text{i}\unicode[STIX]{x1D716}{\displaystyle \frac{\unicode[STIX]{x1D714}\unicode[STIX]{x1D6FA}}{\unicode[STIX]{x1D714}_{0}^{2}-\unicode[STIX]{x1D6FA}^{2}}}{\displaystyle \frac{\unicode[STIX]{x1D6FD}\tan \unicode[STIX]{x1D703}}{z}}\\[11.0pt] \unicode[STIX]{x1D608}_{33}={\displaystyle \frac{\unicode[STIX]{x1D714}^{2}}{\unicode[STIX]{x1D6FE}^{2}\unicode[STIX]{x1D714}_{0}^{2}}}+{\displaystyle \frac{\unicode[STIX]{x1D714}^{2}}{\unicode[STIX]{x1D714}_{0}^{2}-\unicode[STIX]{x1D6FA}^{2}}}\left({\displaystyle \frac{\unicode[STIX]{x1D6FD}\tan \unicode[STIX]{x1D703}}{z}}\right)^{2},\quad \unicode[STIX]{x1D608}_{13}={\displaystyle \frac{\unicode[STIX]{x1D714}_{0}\unicode[STIX]{x1D714}}{\unicode[STIX]{x1D714}_{0}^{2}-\unicode[STIX]{x1D6FA}^{2}}}{\displaystyle \frac{\unicode[STIX]{x1D6FD}\tan \unicode[STIX]{x1D703}}{z}},\end{array}\right\} & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}l@{}}\unicode[STIX]{x1D608}_{11}={\displaystyle \frac{\unicode[STIX]{x1D714}_{0}^{2}}{\unicode[STIX]{x1D714}_{0}^{2}-\unicode[STIX]{x1D6FA}^{2}}},\quad \unicode[STIX]{x1D608}_{12}=\text{i}\unicode[STIX]{x1D716}{\displaystyle \frac{\unicode[STIX]{x1D714}_{0}\unicode[STIX]{x1D6FA}}{\unicode[STIX]{x1D714}_{0}^{2}-\unicode[STIX]{x1D6FA}^{2}}},\quad \unicode[STIX]{x1D608}_{23}=-\text{i}\unicode[STIX]{x1D716}{\displaystyle \frac{\unicode[STIX]{x1D714}\unicode[STIX]{x1D6FA}}{\unicode[STIX]{x1D714}_{0}^{2}-\unicode[STIX]{x1D6FA}^{2}}}{\displaystyle \frac{\unicode[STIX]{x1D6FD}\tan \unicode[STIX]{x1D703}}{z}}\\[11.0pt] \unicode[STIX]{x1D608}_{33}={\displaystyle \frac{\unicode[STIX]{x1D714}^{2}}{\unicode[STIX]{x1D6FE}^{2}\unicode[STIX]{x1D714}_{0}^{2}}}+{\displaystyle \frac{\unicode[STIX]{x1D714}^{2}}{\unicode[STIX]{x1D714}_{0}^{2}-\unicode[STIX]{x1D6FA}^{2}}}\left({\displaystyle \frac{\unicode[STIX]{x1D6FD}\tan \unicode[STIX]{x1D703}}{z}}\right)^{2},\quad \unicode[STIX]{x1D608}_{13}={\displaystyle \frac{\unicode[STIX]{x1D714}_{0}\unicode[STIX]{x1D714}}{\unicode[STIX]{x1D714}_{0}^{2}-\unicode[STIX]{x1D6FA}^{2}}}{\displaystyle \frac{\unicode[STIX]{x1D6FD}\tan \unicode[STIX]{x1D703}}{z}},\end{array}\right\} & & \displaystyle\end{eqnarray}$$
with
![]() $\unicode[STIX]{x1D608}_{22}=\unicode[STIX]{x1D608}_{11}$
,
$\unicode[STIX]{x1D608}_{22}=\unicode[STIX]{x1D608}_{11}$
,
![]() $\unicode[STIX]{x1D608}_{31}=\unicode[STIX]{x1D608}_{13}$
,
$\unicode[STIX]{x1D608}_{31}=\unicode[STIX]{x1D608}_{13}$
,
![]() $\unicode[STIX]{x1D608}_{21}=-\unicode[STIX]{x1D608}_{12}$
,
$\unicode[STIX]{x1D608}_{21}=-\unicode[STIX]{x1D608}_{12}$
,
![]() $\unicode[STIX]{x1D608}_{32}=-\unicode[STIX]{x1D608}_{23}$
,
$\unicode[STIX]{x1D608}_{32}=-\unicode[STIX]{x1D608}_{23}$
,
![]() $\unicode[STIX]{x1D714}_{0}=\unicode[STIX]{x1D714}-k_{\Vert }v_{\Vert }=\unicode[STIX]{x1D714}(z-\unicode[STIX]{x1D6FD})/z$
and
$\unicode[STIX]{x1D714}_{0}=\unicode[STIX]{x1D714}-k_{\Vert }v_{\Vert }=\unicode[STIX]{x1D714}(z-\unicode[STIX]{x1D6FD})/z$
and
![]() $\unicode[STIX]{x1D6FA}=\unicode[STIX]{x1D6FA}_{\text{e}}/\unicode[STIX]{x1D6FE}$
, where
$\unicode[STIX]{x1D6FA}=\unicode[STIX]{x1D6FA}_{\text{e}}/\unicode[STIX]{x1D6FE}$
, where
![]() $\unicode[STIX]{x1D6FA}_{\text{e}}=eB/m$
is the electron cyclotron frequency.
$\unicode[STIX]{x1D6FA}_{\text{e}}=eB/m$
is the electron cyclotron frequency.
A.2 Low-frequency and non-gyrotropic approximations
The expression (A 1) with (A 4) is exact for a 1-D distribution, and simplifying assumptions and approximations need to be made in applying it to a pulsar plasma. One simplifying assumption is that there is a single distribution of pairs; this assumption, which is made here, needs to be relaxed to discuss any beam-driven instability. Two other simplifying approximations are made here: the low-frequency limit and the non-gyrotropic approximation.
A.2.1 Low-frequency limit
Pulsar radio emission is thought to be generated in regions where the wave frequency is much smaller than the cyclotron frequency. We assume the low-frequency approximation in the form
![]() $\unicode[STIX]{x1D714}_{0}\ll \unicode[STIX]{x1D6FA}$
. On expanding in
$\unicode[STIX]{x1D714}_{0}\ll \unicode[STIX]{x1D6FA}$
. On expanding in
![]() $\unicode[STIX]{x1D714}_{0}/\unicode[STIX]{x1D6FA}$
, the leading terms in the non-gyrotropic components are, for a 1-D distribution,
$\unicode[STIX]{x1D714}_{0}/\unicode[STIX]{x1D6FA}$
, the leading terms in the non-gyrotropic components are, for a 1-D distribution,
 $$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}l@{}}\unicode[STIX]{x1D608}_{11}=\unicode[STIX]{x1D608}_{22}=-{\displaystyle \frac{\unicode[STIX]{x1D6FE}^{2}\unicode[STIX]{x1D714}^{2}}{\unicode[STIX]{x1D6FA}_{\text{e}}^{2}}}\left({\displaystyle \frac{z-\unicode[STIX]{x1D6FD}}{z}}\right)^{2},\quad \unicode[STIX]{x1D608}_{13}=\unicode[STIX]{x1D608}_{31}=-{\displaystyle \frac{\unicode[STIX]{x1D6FE}^{2}\unicode[STIX]{x1D714}^{2}}{\unicode[STIX]{x1D6FA}_{\text{e}}^{2}}}{\displaystyle \frac{z-\unicode[STIX]{x1D6FD}}{z}}{\displaystyle \frac{\unicode[STIX]{x1D6FD}\tan \unicode[STIX]{x1D703}}{z}},\\[11.0pt] \unicode[STIX]{x1D608}_{33}=\left(\frac{z}{\unicode[STIX]{x1D6FE}(z-\unicode[STIX]{x1D6FD})}\right)^{2}-{\displaystyle \frac{\unicode[STIX]{x1D6FE}^{2}\unicode[STIX]{x1D714}^{2}}{\unicode[STIX]{x1D6FA}_{\text{e}}^{2}}}\left({\displaystyle \frac{\unicode[STIX]{x1D6FD}\tan \unicode[STIX]{x1D703}}{z}}\right)^{2}.\end{array}\right\} & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}l@{}}\unicode[STIX]{x1D608}_{11}=\unicode[STIX]{x1D608}_{22}=-{\displaystyle \frac{\unicode[STIX]{x1D6FE}^{2}\unicode[STIX]{x1D714}^{2}}{\unicode[STIX]{x1D6FA}_{\text{e}}^{2}}}\left({\displaystyle \frac{z-\unicode[STIX]{x1D6FD}}{z}}\right)^{2},\quad \unicode[STIX]{x1D608}_{13}=\unicode[STIX]{x1D608}_{31}=-{\displaystyle \frac{\unicode[STIX]{x1D6FE}^{2}\unicode[STIX]{x1D714}^{2}}{\unicode[STIX]{x1D6FA}_{\text{e}}^{2}}}{\displaystyle \frac{z-\unicode[STIX]{x1D6FD}}{z}}{\displaystyle \frac{\unicode[STIX]{x1D6FD}\tan \unicode[STIX]{x1D703}}{z}},\\[11.0pt] \unicode[STIX]{x1D608}_{33}=\left(\frac{z}{\unicode[STIX]{x1D6FE}(z-\unicode[STIX]{x1D6FD})}\right)^{2}-{\displaystyle \frac{\unicode[STIX]{x1D6FE}^{2}\unicode[STIX]{x1D714}^{2}}{\unicode[STIX]{x1D6FA}_{\text{e}}^{2}}}\left({\displaystyle \frac{\unicode[STIX]{x1D6FD}\tan \unicode[STIX]{x1D703}}{z}}\right)^{2}.\end{array}\right\} & & \displaystyle\end{eqnarray}$$
On averaging over the distribution function, the term
![]() $\propto 1/(z-\unicode[STIX]{x1D6FD})^{2}$
leads to the RPDF discussed below, and the other terms involve
$\propto 1/(z-\unicode[STIX]{x1D6FD})^{2}$
leads to the RPDF discussed below, and the other terms involve
![]() $\langle \unicode[STIX]{x1D6FE}\rangle ,\langle \unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FD}\rangle ,\langle \unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FD}^{2}\rangle$
. A simplifying assumption in the rest frame is that
$\langle \unicode[STIX]{x1D6FE}\rangle ,\langle \unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FD}\rangle ,\langle \unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FD}^{2}\rangle$
. A simplifying assumption in the rest frame is that
![]() $g(-u)=g(u)$
is an even function, implying
$g(-u)=g(u)$
is an even function, implying
![]() $\langle \unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FD}\rangle =0$
. One has
$\langle \unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FD}\rangle =0$
. One has
![]() $\langle \unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FD}^{2}\rangle =\langle \unicode[STIX]{x1D6FE}\rangle -\langle 1/\unicode[STIX]{x1D6FE}\rangle \approx \langle \unicode[STIX]{x1D6FE}\rangle$
for
$\langle \unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FD}^{2}\rangle =\langle \unicode[STIX]{x1D6FE}\rangle -\langle 1/\unicode[STIX]{x1D6FE}\rangle \approx \langle \unicode[STIX]{x1D6FE}\rangle$
for
![]() $\langle \unicode[STIX]{x1D6FE}\rangle \gg 1$
. It follows that for
$\langle \unicode[STIX]{x1D6FE}\rangle \gg 1$
. It follows that for
![]() $\langle \unicode[STIX]{x1D6FE}\rangle \gg 1$
, apart from the RPDF, the only important average is
$\langle \unicode[STIX]{x1D6FE}\rangle \gg 1$
, apart from the RPDF, the only important average is
![]() $\langle \unicode[STIX]{x1D6FE}\rangle$
.
$\langle \unicode[STIX]{x1D6FE}\rangle$
.
A.2.2 Non-gyrotropic approximation
The gyrotropic terms,
![]() $\unicode[STIX]{x1D608}_{12}=-\unicode[STIX]{x1D608}_{21}$
,
$\unicode[STIX]{x1D608}_{12}=-\unicode[STIX]{x1D608}_{21}$
,
![]() $\unicode[STIX]{x1D608}_{32}=-\unicode[STIX]{x1D608}_{23}$
, in the low-frequency approximation are given by
$\unicode[STIX]{x1D608}_{32}=-\unicode[STIX]{x1D608}_{23}$
, in the low-frequency approximation are given by
After substitution into (A 1) these terms are summed over the electrons and positrons giving contributions proportional to
![]() $(n_{+}-n_{-})$
and
$(n_{+}-n_{-})$
and
![]() $(n_{+}\langle \unicode[STIX]{x1D6FD}\rangle _{+}-n_{-}\langle \unicode[STIX]{x1D6FD}\rangle _{-})$
, that is to the charge density and current density, respectively, both of which are non-zero in a pulsar plasma. However, these terms may be regarded as of first order, in comparison with the terms in (A 5), in an expansion in
$(n_{+}\langle \unicode[STIX]{x1D6FD}\rangle _{+}-n_{-}\langle \unicode[STIX]{x1D6FD}\rangle _{-})$
, that is to the charge density and current density, respectively, both of which are non-zero in a pulsar plasma. However, these terms may be regarded as of first order, in comparison with the terms in (A 5), in an expansion in
![]() $1/\unicode[STIX]{x1D705}$
, where
$1/\unicode[STIX]{x1D705}$
, where
![]() $\unicode[STIX]{x1D705}=(n_{+}+n_{-})/|n_{+}-n_{-}|$
is the multiplicity, and then these terms contribute to the dispersion equation only to second order in
$\unicode[STIX]{x1D705}=(n_{+}+n_{-})/|n_{+}-n_{-}|$
is the multiplicity, and then these terms contribute to the dispersion equation only to second order in
![]() $1/\unicode[STIX]{x1D705}$
. The non-gyrotropic approximation corresponds to neglecting the gyrotropic terms. This is equivalent to assuming that the distribution functions for the electrons and positrons are identical,
$1/\unicode[STIX]{x1D705}$
. The non-gyrotropic approximation corresponds to neglecting the gyrotropic terms. This is equivalent to assuming that the distribution functions for the electrons and positrons are identical,
![]() $g_{+}(u)=g_{-}(u)$
. The subscript
$g_{+}(u)=g_{-}(u)$
. The subscript
![]() $\unicode[STIX]{x1D716}$
is redundant in the non-gyrotropic approximation, and is omitted in the following discussion. It is essential to relax the non-gyrotropic assumption in order to discuss the ellipticity of the polarization of the natural modes (e.g. Luo, Melrose & Fussell Reference Luo, Melrose and Fussell2002; Luo & Melrose Reference Luo, Melrose, Camilo and Gaensler2004; Beskin & Philippov Reference Beskin and Philippov2012), but we do not do so here.
$\unicode[STIX]{x1D716}$
is redundant in the non-gyrotropic approximation, and is omitted in the following discussion. It is essential to relax the non-gyrotropic assumption in order to discuss the ellipticity of the polarization of the natural modes (e.g. Luo, Melrose & Fussell Reference Luo, Melrose and Fussell2002; Luo & Melrose Reference Luo, Melrose, Camilo and Gaensler2004; Beskin & Philippov Reference Beskin and Philippov2012), but we do not do so here.
A.2.3 Dielectric tensor for pulsar plasma
With these assumptions, the non-gyrotropic components of the dielectric tensor in the rest frame of a pulsar plasma reduce to,
![]() $\unicode[STIX]{x1D612}_{ij}(\unicode[STIX]{x1D714},\boldsymbol{k})\rightarrow \unicode[STIX]{x1D612}_{ij}$
, (Melrose et al.
Reference Melrose, Gedalin, Kennett and Fletcher1999)
$\unicode[STIX]{x1D612}_{ij}(\unicode[STIX]{x1D714},\boldsymbol{k})\rightarrow \unicode[STIX]{x1D612}_{ij}$
, (Melrose et al.
Reference Melrose, Gedalin, Kennett and Fletcher1999)
 $$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}l@{}}\unicode[STIX]{x1D612}_{11}=\unicode[STIX]{x1D612}_{22}=1+{\displaystyle \frac{\unicode[STIX]{x1D714}_{\text{p}}^{2}}{\unicode[STIX]{x1D6FA}_{e}^{2}}}{\displaystyle \frac{1}{z^{2}}}\langle \unicode[STIX]{x1D6FE}(z-\unicode[STIX]{x1D6FD})^{2}\rangle ,\quad \unicode[STIX]{x1D612}_{13}=\unicode[STIX]{x1D612}_{31}={\displaystyle \frac{\unicode[STIX]{x1D714}_{\text{p}}^{2}}{\unicode[STIX]{x1D6FA}_{e}^{2}}}{\displaystyle \frac{\tan \unicode[STIX]{x1D703}}{z^{2}}}\langle \unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FD}(z-\unicode[STIX]{x1D6FD})\rangle ,\\ \unicode[STIX]{x1D612}_{33}=1-{\displaystyle \frac{\unicode[STIX]{x1D714}_{\text{p}}^{2}}{\unicode[STIX]{x1D714}^{2}}}z^{2}W(z)+{\displaystyle \frac{\unicode[STIX]{x1D714}_{\text{p}}^{2}}{\unicode[STIX]{x1D6FA}_{e}^{2}}}{\displaystyle \frac{\tan ^{2}\unicode[STIX]{x1D703}}{z^{2}}}\langle \unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FD}^{2}\rangle .\end{array}\right\} & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}l@{}}\unicode[STIX]{x1D612}_{11}=\unicode[STIX]{x1D612}_{22}=1+{\displaystyle \frac{\unicode[STIX]{x1D714}_{\text{p}}^{2}}{\unicode[STIX]{x1D6FA}_{e}^{2}}}{\displaystyle \frac{1}{z^{2}}}\langle \unicode[STIX]{x1D6FE}(z-\unicode[STIX]{x1D6FD})^{2}\rangle ,\quad \unicode[STIX]{x1D612}_{13}=\unicode[STIX]{x1D612}_{31}={\displaystyle \frac{\unicode[STIX]{x1D714}_{\text{p}}^{2}}{\unicode[STIX]{x1D6FA}_{e}^{2}}}{\displaystyle \frac{\tan \unicode[STIX]{x1D703}}{z^{2}}}\langle \unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FD}(z-\unicode[STIX]{x1D6FD})\rangle ,\\ \unicode[STIX]{x1D612}_{33}=1-{\displaystyle \frac{\unicode[STIX]{x1D714}_{\text{p}}^{2}}{\unicode[STIX]{x1D714}^{2}}}z^{2}W(z)+{\displaystyle \frac{\unicode[STIX]{x1D714}_{\text{p}}^{2}}{\unicode[STIX]{x1D6FA}_{e}^{2}}}{\displaystyle \frac{\tan ^{2}\unicode[STIX]{x1D703}}{z^{2}}}\langle \unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FD}^{2}\rangle .\end{array}\right\} & & \displaystyle\end{eqnarray}$$
The RPDF
![]() $W(z)$
is defined by
$W(z)$
is defined by
In the rest frame of the plasma
![]() $g(u)$
is an even function of
$g(u)$
is an even function of
![]() $\unicode[STIX]{x1D6FD}$
which then implies that (A 7) may be expressed as
$\unicode[STIX]{x1D6FD}$
which then implies that (A 7) may be expressed as
 $$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}l@{}}\unicode[STIX]{x1D612}_{11}=\unicode[STIX]{x1D612}_{22}=1+{\displaystyle \frac{1}{\unicode[STIX]{x1D6FD}_{\text{A}}^{2}}}\left(1+{\displaystyle \frac{\unicode[STIX]{x0394}\unicode[STIX]{x1D6FD}^{2}}{z^{2}}}\right),\quad \unicode[STIX]{x1D612}_{33}=1-{\displaystyle \frac{\unicode[STIX]{x1D714}_{\text{p}}^{2}}{\unicode[STIX]{x1D714}^{2}}}z^{2}W(z)+{\displaystyle \frac{\unicode[STIX]{x0394}\unicode[STIX]{x1D6FD}^{2}\tan ^{2}\unicode[STIX]{x1D703}}{\unicode[STIX]{x1D6FD}_{\text{A}}^{2}z^{2}}},\\[12.0pt] \unicode[STIX]{x1D612}_{13}=\unicode[STIX]{x1D612}_{31}=-{\displaystyle \frac{\unicode[STIX]{x0394}\unicode[STIX]{x1D6FD}^{2}\tan \unicode[STIX]{x1D703}}{\unicode[STIX]{x1D6FD}_{\text{A}}^{2}z^{2}}},\quad \unicode[STIX]{x1D6FD}_{\text{A}}^{2}={\displaystyle \frac{\unicode[STIX]{x1D6FA}_{\text{e}}^{2}}{\unicode[STIX]{x1D714}_{\text{p}}^{2}\langle \unicode[STIX]{x1D6FE}\rangle }},\quad \unicode[STIX]{x0394}\unicode[STIX]{x1D6FD}^{2}={\displaystyle \frac{\langle \unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FD}^{2}\rangle }{\langle \unicode[STIX]{x1D6FE}\rangle }}=1-{\displaystyle \frac{\langle \unicode[STIX]{x1D6FE}^{-1}\rangle }{\langle \unicode[STIX]{x1D6FE}\rangle }},\end{array}\right\} & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}l@{}}\unicode[STIX]{x1D612}_{11}=\unicode[STIX]{x1D612}_{22}=1+{\displaystyle \frac{1}{\unicode[STIX]{x1D6FD}_{\text{A}}^{2}}}\left(1+{\displaystyle \frac{\unicode[STIX]{x0394}\unicode[STIX]{x1D6FD}^{2}}{z^{2}}}\right),\quad \unicode[STIX]{x1D612}_{33}=1-{\displaystyle \frac{\unicode[STIX]{x1D714}_{\text{p}}^{2}}{\unicode[STIX]{x1D714}^{2}}}z^{2}W(z)+{\displaystyle \frac{\unicode[STIX]{x0394}\unicode[STIX]{x1D6FD}^{2}\tan ^{2}\unicode[STIX]{x1D703}}{\unicode[STIX]{x1D6FD}_{\text{A}}^{2}z^{2}}},\\[12.0pt] \unicode[STIX]{x1D612}_{13}=\unicode[STIX]{x1D612}_{31}=-{\displaystyle \frac{\unicode[STIX]{x0394}\unicode[STIX]{x1D6FD}^{2}\tan \unicode[STIX]{x1D703}}{\unicode[STIX]{x1D6FD}_{\text{A}}^{2}z^{2}}},\quad \unicode[STIX]{x1D6FD}_{\text{A}}^{2}={\displaystyle \frac{\unicode[STIX]{x1D6FA}_{\text{e}}^{2}}{\unicode[STIX]{x1D714}_{\text{p}}^{2}\langle \unicode[STIX]{x1D6FE}\rangle }},\quad \unicode[STIX]{x0394}\unicode[STIX]{x1D6FD}^{2}={\displaystyle \frac{\langle \unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FD}^{2}\rangle }{\langle \unicode[STIX]{x1D6FE}\rangle }}=1-{\displaystyle \frac{\langle \unicode[STIX]{x1D6FE}^{-1}\rangle }{\langle \unicode[STIX]{x1D6FE}\rangle }},\end{array}\right\} & & \displaystyle\end{eqnarray}$$
where we use
![]() $\langle Q\rangle =0$
for
$\langle Q\rangle =0$
for
![]() $Q$
any odd function of
$Q$
any odd function of
![]() $\unicode[STIX]{x1D6FD}$
.
$\unicode[STIX]{x1D6FD}$
.
A.3 Dispersion equation for a pulsar plasma
The dispersion equation for waves in a plasma is given by setting the determinant of the matrix form of
![]() $\unicode[STIX]{x1D6EC}_{ij}$
to zero. The non-zero components of
$\unicode[STIX]{x1D6EC}_{ij}$
to zero. The non-zero components of
![]() $\unicode[STIX]{x1D6EC}_{ij}$
are obtained using (2.1) and (A 7) as
$\unicode[STIX]{x1D6EC}_{ij}$
are obtained using (2.1) and (A 7) as
 $$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}l@{}}\unicode[STIX]{x1D6EC}_{11}=1-{\displaystyle \frac{1}{z^{2}}}+{\displaystyle \frac{\unicode[STIX]{x1D714}_{\text{p}}^{2}}{\unicode[STIX]{x1D6FA}_{e}^{2}}}{\displaystyle \frac{1}{z^{2}}}\langle \unicode[STIX]{x1D6FE}(z-\unicode[STIX]{x1D6FD})^{2}\rangle ,\quad \unicode[STIX]{x1D6EC}_{13}={\displaystyle \frac{\tan \unicode[STIX]{x1D703}}{z^{2}}}\left[1+{\displaystyle \frac{\unicode[STIX]{x1D714}_{\text{p}}^{2}}{\unicode[STIX]{x1D6FA}_{e}^{2}}}\langle \unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FD}(z-\unicode[STIX]{x1D6FD})\rangle \right],\\[16.0pt] \unicode[STIX]{x1D6EC}_{22}=\unicode[STIX]{x1D6EC}_{11}-{\displaystyle \frac{\tan ^{2}\unicode[STIX]{x1D703}}{z^{2}}},\quad \unicode[STIX]{x1D6EC}_{33}=1-{\displaystyle \frac{\unicode[STIX]{x1D714}_{\text{p}}^{2}}{\unicode[STIX]{x1D714}^{2}}}z^{2}W(z)-{\displaystyle \frac{\tan ^{2}\unicode[STIX]{x1D703}}{z^{2}}}\left[1-{\displaystyle \frac{\unicode[STIX]{x1D714}_{\text{p}}^{2}}{\unicode[STIX]{x1D6FA}_{e}^{2}}}\langle \unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FD}^{2}\rangle \right],\end{array}\right\}\quad & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}l@{}}\unicode[STIX]{x1D6EC}_{11}=1-{\displaystyle \frac{1}{z^{2}}}+{\displaystyle \frac{\unicode[STIX]{x1D714}_{\text{p}}^{2}}{\unicode[STIX]{x1D6FA}_{e}^{2}}}{\displaystyle \frac{1}{z^{2}}}\langle \unicode[STIX]{x1D6FE}(z-\unicode[STIX]{x1D6FD})^{2}\rangle ,\quad \unicode[STIX]{x1D6EC}_{13}={\displaystyle \frac{\tan \unicode[STIX]{x1D703}}{z^{2}}}\left[1+{\displaystyle \frac{\unicode[STIX]{x1D714}_{\text{p}}^{2}}{\unicode[STIX]{x1D6FA}_{e}^{2}}}\langle \unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FD}(z-\unicode[STIX]{x1D6FD})\rangle \right],\\[16.0pt] \unicode[STIX]{x1D6EC}_{22}=\unicode[STIX]{x1D6EC}_{11}-{\displaystyle \frac{\tan ^{2}\unicode[STIX]{x1D703}}{z^{2}}},\quad \unicode[STIX]{x1D6EC}_{33}=1-{\displaystyle \frac{\unicode[STIX]{x1D714}_{\text{p}}^{2}}{\unicode[STIX]{x1D714}^{2}}}z^{2}W(z)-{\displaystyle \frac{\tan ^{2}\unicode[STIX]{x1D703}}{z^{2}}}\left[1-{\displaystyle \frac{\unicode[STIX]{x1D714}_{\text{p}}^{2}}{\unicode[STIX]{x1D6FA}_{e}^{2}}}\langle \unicode[STIX]{x1D6FE}\unicode[STIX]{x1D6FD}^{2}\rangle \right],\end{array}\right\}\quad & & \displaystyle\end{eqnarray}$$
with
![]() $\unicode[STIX]{x1D6EC}_{31}=\unicode[STIX]{x1D6EC}_{13}$
. Noting that
$\unicode[STIX]{x1D6EC}_{31}=\unicode[STIX]{x1D6EC}_{13}$
. Noting that
![]() $\langle Q\rangle =0$
if
$\langle Q\rangle =0$
if
![]() $Q$
is an odd function of
$Q$
is an odd function of
![]() $\unicode[STIX]{x1D6FD}$
allows us to write (A 10) as
$\unicode[STIX]{x1D6FD}$
allows us to write (A 10) as
 $$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}l@{}}\unicode[STIX]{x1D6EC}_{11}=a-{\displaystyle \frac{b}{z^{2}}},\quad \unicode[STIX]{x1D6EC}_{22}=\unicode[STIX]{x1D6EC}_{11}-{\displaystyle \frac{\tan ^{2}\unicode[STIX]{x1D703}}{z^{2}}},\quad \unicode[STIX]{x1D6EC}_{33}=1-{\displaystyle \frac{\unicode[STIX]{x1D714}_{\text{p}}^{2}}{\unicode[STIX]{x1D714}^{2}}}z^{2}W(z)-{\displaystyle \frac{b\tan ^{2}\unicode[STIX]{x1D703}}{z^{2}}},\\[12.0pt] \unicode[STIX]{x1D6EC}_{13}={\displaystyle \frac{b\tan \unicode[STIX]{x1D703}}{z^{2}}},\quad a=1+{\displaystyle \frac{1}{\unicode[STIX]{x1D6FD}_{\text{A}}^{2}}},\quad b=1-{\displaystyle \frac{\unicode[STIX]{x0394}\unicode[STIX]{x1D6FD}^{2}}{\unicode[STIX]{x1D6FD}_{\text{A}}^{2}}},\quad z_{\text{A}}^{2}={\displaystyle \frac{b}{a}}={\displaystyle \frac{\unicode[STIX]{x1D6FD}_{\text{A}}^{2}-\unicode[STIX]{x0394}\unicode[STIX]{x1D6FD}^{2}}{1+\unicode[STIX]{x1D6FD}_{\text{A}}^{2}}}.\end{array}\right\}\quad & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}l@{}}\unicode[STIX]{x1D6EC}_{11}=a-{\displaystyle \frac{b}{z^{2}}},\quad \unicode[STIX]{x1D6EC}_{22}=\unicode[STIX]{x1D6EC}_{11}-{\displaystyle \frac{\tan ^{2}\unicode[STIX]{x1D703}}{z^{2}}},\quad \unicode[STIX]{x1D6EC}_{33}=1-{\displaystyle \frac{\unicode[STIX]{x1D714}_{\text{p}}^{2}}{\unicode[STIX]{x1D714}^{2}}}z^{2}W(z)-{\displaystyle \frac{b\tan ^{2}\unicode[STIX]{x1D703}}{z^{2}}},\\[12.0pt] \unicode[STIX]{x1D6EC}_{13}={\displaystyle \frac{b\tan \unicode[STIX]{x1D703}}{z^{2}}},\quad a=1+{\displaystyle \frac{1}{\unicode[STIX]{x1D6FD}_{\text{A}}^{2}}},\quad b=1-{\displaystyle \frac{\unicode[STIX]{x0394}\unicode[STIX]{x1D6FD}^{2}}{\unicode[STIX]{x1D6FD}_{\text{A}}^{2}}},\quad z_{\text{A}}^{2}={\displaystyle \frac{b}{a}}={\displaystyle \frac{\unicode[STIX]{x1D6FD}_{\text{A}}^{2}-\unicode[STIX]{x0394}\unicode[STIX]{x1D6FD}^{2}}{1+\unicode[STIX]{x1D6FD}_{\text{A}}^{2}}}.\end{array}\right\}\quad & & \displaystyle\end{eqnarray}$$
The parameter
![]() $z_{\text{A}}$
may be interpreted as the relativistic Alfvén speed. The Lorentz factor corresponding to this speed is
$z_{\text{A}}$
may be interpreted as the relativistic Alfvén speed. The Lorentz factor corresponding to this speed is
![]() $\unicode[STIX]{x1D6FE}_{\text{A}}$
, given by
$\unicode[STIX]{x1D6FE}_{\text{A}}$
, given by
with
![]() $\unicode[STIX]{x1D6FE}_{\text{A}}\approx \unicode[STIX]{x1D6FD}_{\text{A}}$
in the highly relativistic limit. Equation (A 11) reproduce expressions given by Melrose et al. (Reference Melrose, Gedalin, Kennett and Fletcher1999), except for the correction of an error in
$\unicode[STIX]{x1D6FE}_{\text{A}}\approx \unicode[STIX]{x1D6FD}_{\text{A}}$
in the highly relativistic limit. Equation (A 11) reproduce expressions given by Melrose et al. (Reference Melrose, Gedalin, Kennett and Fletcher1999), except for the correction of an error in
![]() $\unicode[STIX]{x1D6EC}_{22}$
(
$\unicode[STIX]{x1D6EC}_{22}$
(
![]() $-\sin ^{2}\unicode[STIX]{x1D703}$
is replaced by
$-\sin ^{2}\unicode[STIX]{x1D703}$
is replaced by
![]() $+\tan ^{2}\unicode[STIX]{x1D703}$
).
$+\tan ^{2}\unicode[STIX]{x1D703}$
).
In the cold-plasma limit,
![]() $\unicode[STIX]{x1D70C}\rightarrow \infty$
and
$\unicode[STIX]{x1D70C}\rightarrow \infty$
and
![]() $\langle \unicode[STIX]{x1D6FE}\rangle \rightarrow 1$
, and infinite magnetic field,
$\langle \unicode[STIX]{x1D6FE}\rangle \rightarrow 1$
, and infinite magnetic field,
![]() $\unicode[STIX]{x1D6FA}_{e}\rightarrow \infty$
and
$\unicode[STIX]{x1D6FA}_{e}\rightarrow \infty$
and
![]() $\unicode[STIX]{x1D6FD}_{A}\rightarrow \infty$
, the expressions in (A 11) may be approximated as
$\unicode[STIX]{x1D6FD}_{A}\rightarrow \infty$
, the expressions in (A 11) may be approximated as
 $$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}l@{}}\unicode[STIX]{x1D6EC}_{11}=a-{\displaystyle \frac{1}{z^{2}}},\quad \unicode[STIX]{x1D6EC}_{22}=\unicode[STIX]{x1D6EC}_{11}-{\displaystyle \frac{\tan ^{2}\unicode[STIX]{x1D703}}{z^{2}}},\quad \unicode[STIX]{x1D6EC}_{33}=1-{\displaystyle \frac{\unicode[STIX]{x1D714}_{\text{p}}^{2}}{\unicode[STIX]{x1D714}^{2}}}-{\displaystyle \frac{\tan ^{2}\unicode[STIX]{x1D703}}{z^{2}}},\\[12.0pt] \unicode[STIX]{x1D6EC}_{13}={\displaystyle \frac{\tan \unicode[STIX]{x1D703}}{z^{2}}},\quad a=1,\quad b=1,\quad z_{\text{A}}^{2}=1,\end{array}\right\} & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \left.\begin{array}{@{}l@{}}\unicode[STIX]{x1D6EC}_{11}=a-{\displaystyle \frac{1}{z^{2}}},\quad \unicode[STIX]{x1D6EC}_{22}=\unicode[STIX]{x1D6EC}_{11}-{\displaystyle \frac{\tan ^{2}\unicode[STIX]{x1D703}}{z^{2}}},\quad \unicode[STIX]{x1D6EC}_{33}=1-{\displaystyle \frac{\unicode[STIX]{x1D714}_{\text{p}}^{2}}{\unicode[STIX]{x1D714}^{2}}}-{\displaystyle \frac{\tan ^{2}\unicode[STIX]{x1D703}}{z^{2}}},\\[12.0pt] \unicode[STIX]{x1D6EC}_{13}={\displaystyle \frac{\tan \unicode[STIX]{x1D703}}{z^{2}}},\quad a=1,\quad b=1,\quad z_{\text{A}}^{2}=1,\end{array}\right\} & & \displaystyle\end{eqnarray}$$
where we use
![]() $z^{2}W(z)\rightarrow 1$
in the cold-plasma limit.
$z^{2}W(z)\rightarrow 1$
in the cold-plasma limit.
Appendix B. RPDF for
 $|z|\leqslant 1$
$|z|\leqslant 1$
We may write the RPDF (A 8) as
where, as per the Landau prescription, we integrate below the singularity at
![]() $\unicode[STIX]{x1D6FD}=z$
in the complex
$\unicode[STIX]{x1D6FD}=z$
in the complex
![]() $\unicode[STIX]{x1D6FD}$
plane. The integral over
$\unicode[STIX]{x1D6FD}$
plane. The integral over
![]() $z-\unicode[STIX]{x1D6FF}\leqslant \unicode[STIX]{x1D6FD}\leqslant z+\unicode[STIX]{x1D6FF}$
is performed in a positive sense and contributes
$z-\unicode[STIX]{x1D6FF}\leqslant \unicode[STIX]{x1D6FD}\leqslant z+\unicode[STIX]{x1D6FF}$
is performed in a positive sense and contributes
![]() $i\unicode[STIX]{x03C0}$
times the residue. The remaining integrals may be partially integrated to give
$i\unicode[STIX]{x03C0}$
times the residue. The remaining integrals may be partially integrated to give
 $$\begin{eqnarray}\displaystyle & & \displaystyle \lim _{\unicode[STIX]{x1D6FF}\rightarrow 0}\left(\int _{-1}^{z-\unicode[STIX]{x1D6FF}}+\int _{z+\unicode[STIX]{x1D6FF}}^{1}\right)\text{d}\unicode[STIX]{x1D6FD}\,{\displaystyle \frac{1}{\unicode[STIX]{x1D6FD}-z}}{\displaystyle \frac{\text{d}g(u)}{\text{d}\unicode[STIX]{x1D6FD}}}\nonumber\\ \displaystyle & & \displaystyle \quad =\lim _{\unicode[STIX]{x1D6FF}\rightarrow 0}\left\{-2{\displaystyle \frac{g(u)|_{\unicode[STIX]{x1D6FD}=z}}{\unicode[STIX]{x1D6FF}}}+\left(\int _{-1}^{z-\unicode[STIX]{x1D6FF}}+\int _{z+\unicode[STIX]{x1D6FF}}^{1}\right)\text{d}\unicode[STIX]{x1D6FD}\,{\displaystyle \frac{g(u)}{(\unicode[STIX]{x1D6FD}-z)^{2}}}\right\},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \lim _{\unicode[STIX]{x1D6FF}\rightarrow 0}\left(\int _{-1}^{z-\unicode[STIX]{x1D6FF}}+\int _{z+\unicode[STIX]{x1D6FF}}^{1}\right)\text{d}\unicode[STIX]{x1D6FD}\,{\displaystyle \frac{1}{\unicode[STIX]{x1D6FD}-z}}{\displaystyle \frac{\text{d}g(u)}{\text{d}\unicode[STIX]{x1D6FD}}}\nonumber\\ \displaystyle & & \displaystyle \quad =\lim _{\unicode[STIX]{x1D6FF}\rightarrow 0}\left\{-2{\displaystyle \frac{g(u)|_{\unicode[STIX]{x1D6FD}=z}}{\unicode[STIX]{x1D6FF}}}+\left(\int _{-1}^{z-\unicode[STIX]{x1D6FF}}+\int _{z+\unicode[STIX]{x1D6FF}}^{1}\right)\text{d}\unicode[STIX]{x1D6FD}\,{\displaystyle \frac{g(u)}{(\unicode[STIX]{x1D6FD}-z)^{2}}}\right\},\end{eqnarray}$$
where we use
![]() $g(u)|_{\unicode[STIX]{x1D6FD}=z\pm \unicode[STIX]{x1D6FF}}\approx g(u)|_{\unicode[STIX]{x1D6FD}=z}$
for sufficiently small
$g(u)|_{\unicode[STIX]{x1D6FD}=z\pm \unicode[STIX]{x1D6FF}}\approx g(u)|_{\unicode[STIX]{x1D6FD}=z}$
for sufficiently small
![]() $\unicode[STIX]{x1D6FF}$
. Noting that
$\unicode[STIX]{x1D6FF}$
. Noting that
then gives (3.2).
Appendix C. Group velocity
Let the dispersion equation,
![]() $\unicode[STIX]{x1D612}_{33}=0$
, for the L mode be written
$\unicode[STIX]{x1D612}_{33}=0$
, for the L mode be written
![]() $K=0$
with
$K=0$
with
The chain rule implies
to be evaluated at
![]() $K=0$
. Using
$K=0$
. Using
![]() $z=\unicode[STIX]{x1D714}/k_{\Vert }c$
and equation (C 1) one finds
$z=\unicode[STIX]{x1D714}/k_{\Vert }c$
and equation (C 1) one finds
The ratio of electric to total energy becomes
The group speed becomes
Appendix D. Approximation of
 $z^{2}W(z)$
$z^{2}W(z)$
For
![]() $z\gg 1$
we may write
$z\gg 1$
we may write
which implies, after swapping the order of integration and summation,
with
 $$\begin{eqnarray}\displaystyle \langle \unicode[STIX]{x1D6FD}^{s}/\unicode[STIX]{x1D6FE}^{3}\rangle =\left\{\begin{array}{@{}ll@{}}\displaystyle \mathop{\sum }_{j=0}^{k}{\displaystyle \frac{k!(-1)^{j}}{(k-j)!j!}}\left\langle {\displaystyle \frac{1}{\unicode[STIX]{x1D6FE}^{2j+3}}}\right\rangle ,\quad & \text{for}~s=2k,\\[12.0pt] 0,\quad & \text{for}~s=2k+1.\end{array}\right. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \langle \unicode[STIX]{x1D6FD}^{s}/\unicode[STIX]{x1D6FE}^{3}\rangle =\left\{\begin{array}{@{}ll@{}}\displaystyle \mathop{\sum }_{j=0}^{k}{\displaystyle \frac{k!(-1)^{j}}{(k-j)!j!}}\left\langle {\displaystyle \frac{1}{\unicode[STIX]{x1D6FE}^{2j+3}}}\right\rangle ,\quad & \text{for}~s=2k,\\[12.0pt] 0,\quad & \text{for}~s=2k+1.\end{array}\right. & & \displaystyle\end{eqnarray}$$
These then give the first case in (5.1).
Expansion about
![]() $z=1$
gives
$z=1$
gives
which implies
The average quantity may be expressed as
Each term inside the sum in (D 6) is then, to highest order in
![]() $\langle \unicode[STIX]{x1D6FE}\rangle \gg 1$
, equal to
$\langle \unicode[STIX]{x1D6FE}\rangle \gg 1$
, equal to
where we use
![]() $\langle \unicode[STIX]{x1D6FE}^{n}\rangle =n!\langle \unicode[STIX]{x1D6FE}\rangle ^{n}$
for
$\langle \unicode[STIX]{x1D6FE}^{n}\rangle =n!\langle \unicode[STIX]{x1D6FE}\rangle ^{n}$
for
![]() $\langle \unicode[STIX]{x1D6FE}\rangle \gg 1$
. The series appears to have a radius of convergence of zero. This leads us to suggest that the approximation given in (5.1) for the case
$\langle \unicode[STIX]{x1D6FE}\rangle \gg 1$
. The series appears to have a radius of convergence of zero. This leads us to suggest that the approximation given in (5.1) for the case
![]() $|1-z|\ll 1$
is at best questionable and that it should not be used.
$|1-z|\ll 1$
is at best questionable and that it should not be used.
Appendix E. List of notations
Table 3. List of common symbols and parameters. The values each parameter takes may vary depending on the context.