No CrossRef data available.
Article contents
Transport equations on different time scales for intermediately and strongly collisional regimes
Published online by Cambridge University Press: 13 March 2009
Abstract
The plasma transport equations for a weakly collisional plasma have previously been derived for four different time scales. This paper is devoted to the derivation of the plasma transport equations for the two other complementary regimes: the intermediately collisional regime (ICR) (i.e. for the case where the transit time w1 is of the same order as the collision time 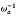 is of the same order as the collision time
is of the same order as the collision time 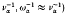 ), and the strongly collisional regime (SCR) (i.e. for the case of
), and the strongly collisional regime (SCR) (i.e. for the case of 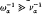 ) for different time scales. It is shown that the lowest-order gyromotion is unperturbed by collisions. On the Alfvén time scale, one merely obtains for both the intermediately collisional case and the strongly collisional case the single-fluid ideal MHD equations, if certain additional requirements are satisfied. On the MHD-collision time scale, one arrives at the full set of transport equations, where in both cases, contrary to the weakly collisional case, no turbulent terms are found. On the resistive diffusion timescale, one ends up with the known transport equations, with the addition of turbulent contributions.
) for different time scales. It is shown that the lowest-order gyromotion is unperturbed by collisions. On the Alfvén time scale, one merely obtains for both the intermediately collisional case and the strongly collisional case the single-fluid ideal MHD equations, if certain additional requirements are satisfied. On the MHD-collision time scale, one arrives at the full set of transport equations, where in both cases, contrary to the weakly collisional case, no turbulent terms are found. On the resistive diffusion timescale, one ends up with the known transport equations, with the addition of turbulent contributions.
- Type
- Research Article
- Information
- Copyright
- Copyright © Cambridge University Press 1996


