1. Introduction
In a plasma, the drag force from Coulomb collisions acting on fast electrons decreases with the electron velocity. Thus, if the electric field
![]() $E$
exceeds a threshold value
$E$
exceeds a threshold value
![]() $E_{c}$
, electrons with sufficient velocity will be indefinitely accelerated and are called runaway electrons. The critical field
$E_{c}$
, electrons with sufficient velocity will be indefinitely accelerated and are called runaway electrons. The critical field
![]() $E_{c}$
is defined as
$E_{c}$
is defined as
where
![]() $n_{e}$
is the electron density,
$n_{e}$
is the electron density,
![]() $m_{e}$
is the electron rest mass,
$m_{e}$
is the electron rest mass,
![]() $c$
is the speed of light,
$c$
is the speed of light,
![]() $e$
is the elementary charge and
$e$
is the elementary charge and
![]() $\ln {\it\Lambda}$
is the Coulomb logarithm.
$\ln {\it\Lambda}$
is the Coulomb logarithm.
Runaway electrons are generated in the presence of an induced electric field parallel to the magnetic field. In a tokamak, the condition
![]() $E>E_{c}$
can be met during the plasma startup, during the flat-top phase of Ohmic plasmas if the density is sufficiently low, or in plasma disruptions. Especially during disruption events, a beam of runaways carrying a current of several MA and an energy of several
$E>E_{c}$
can be met during the plasma startup, during the flat-top phase of Ohmic plasmas if the density is sufficiently low, or in plasma disruptions. Especially during disruption events, a beam of runaways carrying a current of several MA and an energy of several
![]() $\text{MJ}$
may form. Such a runaway beam would pose a serious threat to the integrity of the first wall in reactor-size fusion devices. Any mechanism that could possibly limit the formation of a considerable runaway beam would be of importance.
$\text{MJ}$
may form. Such a runaway beam would pose a serious threat to the integrity of the first wall in reactor-size fusion devices. Any mechanism that could possibly limit the formation of a considerable runaway beam would be of importance.
While the role of radiative momentum losses due to synchrotron emission was studied previously in Andersson, Helander & Eriksson (Reference Andersson, Helander and Eriksson2001), the possibility of a non-monotonic feature in the energy distribution of runaways – which we will henceforth refer to as a ‘bump’ – was not considered. The formulation of the problem in Andersson et al. (Reference Andersson, Helander and Eriksson2001) does not ensure particle conservation in the presence of radiation reaction and neglects certain terms needed to describe the bump (Hazeltine & Mahajan Reference Hazeltine and Mahajan2004; Stahl et al. Reference Stahl, Hirvijoki, Decker, Embréus and Fülöp2015). The possibility of bump formation, however, immediately raises the question of whether the non-monotonic behaviour of the distribution could lead to kinetic instabilities, causing a redistribution of the runaway particles, favourable for mitigating the potential threat to the machine. A thorough investigation of conditions favouring bump formation is thus needed.
In the present paper, we use analytical calculations to investigate the runaway electron distribution under the combined influence of Coulomb collisions, electric field acceleration and radiative momentum losses. We show the existence of a bump and derive both a threshold condition for the appearance of the bump and an approximate expression for its location in parallel momentum space. The accuracy of the analytical estimates is then tested against numerical simulations carried out using CODE (Landreman, Stahl & Fülöp Reference Landreman, Stahl and Fülöp2014; Stahl et al. Reference Stahl, Hirvijoki, Decker, Embréus and Fülöp2015).
The paper is organized as follows. In § 2, we start by describing the particle phase-space kinetic equation. We also discuss the transformation of the kinetic equation into the guiding-centre phase space and give the corresponding expression in the case of a uniform plasma. Analytical calculation of the condition for bump-on-tail appearance, based on the guiding-centre dynamics, is presented in § 3. A comparison of the derived conditions with numerical results is presented in § 4, before we conclude in § 5.
2. Kinetic equation
The kinetic equation describing the dynamics of charged particles in a plasma is
where
![]() $C[\,f_{a},f_{b}]$
is the collision operator for collisions between particle species
$C[\,f_{a},f_{b}]$
is the collision operator for collisions between particle species
![]() $a$
and
$a$
and
![]() $b$
,
$b$
,
![]() $z^{{\it\alpha}}=(\boldsymbol{x},\boldsymbol{p})$
are the phase-space coordinates and
$z^{{\it\alpha}}=(\boldsymbol{x},\boldsymbol{p})$
are the phase-space coordinates and
![]() ${\dot{z}}^{{\it\alpha}}=(\dot{\boldsymbol{x}},\dot{\boldsymbol{p}})$
are the equations of motion. In the Fokker–Planck limit, the Coulomb collision operator is given by
${\dot{z}}^{{\it\alpha}}=(\dot{\boldsymbol{x}},\dot{\boldsymbol{p}})$
are the equations of motion. In the Fokker–Planck limit, the Coulomb collision operator is given by
where
![]() $\boldsymbol{K}_{ab}[\,f_{b}]$
is the friction vector and
$\boldsymbol{K}_{ab}[\,f_{b}]$
is the friction vector and
![]() $\unicode[STIX]{x1D63F}_{ab}[\,f_{b}]$
is the diffusion tensor (see appendix A for details). In this paper, we do not consider contributions from large-angle collisions.
$\unicode[STIX]{x1D63F}_{ab}[\,f_{b}]$
is the diffusion tensor (see appendix A for details). In this paper, we do not consider contributions from large-angle collisions.
The equations of motion for a particle with charge
![]() $q$
and mass
$q$
and mass
![]() $m$
combine the Hamiltonian motion from the electric and magnetic fields
$m$
combine the Hamiltonian motion from the electric and magnetic fields
![]() $\boldsymbol{E}$
and
$\boldsymbol{E}$
and
![]() $\boldsymbol{B}$
, and a force
$\boldsymbol{B}$
, and a force
![]() $\boldsymbol{F}$
that accounts for non-Hamiltonian dynamics,
$\boldsymbol{F}$
that accounts for non-Hamiltonian dynamics,
The LAD force does, however, contain third-order time derivatives of the particle position, which allows for the existence of pathological solutions. For instance, the particle velocity may grow exponentially in the absence of external forces (
![]() $\boldsymbol{E}=0$
,
$\boldsymbol{E}=0$
,
![]() $\boldsymbol{B}=0$
), see e.g. Rohrlich (Reference Rohrlich2007). These issues have generated discussion regarding which expression to use for the RR force. Landau & Lifshitz (Reference Landau and Lifshitz1975) suggested a perturbative approach in which the velocity derivatives in (2.5) are expressed in terms of the external force only (here the Lorentz force). Ford & O’Connell (Reference Ford and O’Connell1993) argue that this approach is in fact the correct one. In the paper by Spohn (Reference Spohn2000), it is shown that the non-physical solutions can be avoided if the LAD force is limited on a so-called critical surface, and that the resulting expressions will be equivalent to those of the perturbative approach. We have thus chosen to adopt the perturbative approach. Furthermore, we neglect the electric field in the expressions for
$\boldsymbol{B}=0$
), see e.g. Rohrlich (Reference Rohrlich2007). These issues have generated discussion regarding which expression to use for the RR force. Landau & Lifshitz (Reference Landau and Lifshitz1975) suggested a perturbative approach in which the velocity derivatives in (2.5) are expressed in terms of the external force only (here the Lorentz force). Ford & O’Connell (Reference Ford and O’Connell1993) argue that this approach is in fact the correct one. In the paper by Spohn (Reference Spohn2000), it is shown that the non-physical solutions can be avoided if the LAD force is limited on a so-called critical surface, and that the resulting expressions will be equivalent to those of the perturbative approach. We have thus chosen to adopt the perturbative approach. Furthermore, we neglect the electric field in the expressions for
![]() $\dot{\boldsymbol{v}}$
and
$\dot{\boldsymbol{v}}$
and
![]() $\ddot{\boldsymbol{v}}$
in the RR force. This is justified since the motion of the particle is dominated by the magnetic field in the strongly magnetized plasmas considered here. An excellent discussion about the RR force can be found in a recent review paper by Di Piazza et al. (Reference Di Piazza, Müller, Hatsagortsyan and Keitel2012).
$\ddot{\boldsymbol{v}}$
in the RR force. This is justified since the motion of the particle is dominated by the magnetic field in the strongly magnetized plasmas considered here. An excellent discussion about the RR force can be found in a recent review paper by Di Piazza et al. (Reference Di Piazza, Müller, Hatsagortsyan and Keitel2012).
2.1. Guiding-centre transformation
Because of the
![]() $\boldsymbol{v}\times \boldsymbol{B}$
term, the particle phase-space kinetic equation in a magnetized plasma includes the rapid gyro-motion time scale which is often not interesting and is expensive to resolve computationally. It can, however, be eliminated using guiding-centre Lie-transform perturbation methods. The transformation of the Hamiltonian equations of motion is one of the classical results in modern plasma physics (see Littlejohn Reference Littlejohn1983; Cary & Brizard Reference Cary and Brizard2009), and the Fokker–Planck collision operator has been considered in Brizard (Reference Brizard2004), Decker et al. (Reference Decker, Peysson, Brizard and Duthoit2010) and Hirvijoki et al. (Reference Hirvijoki, Brizard, Snicker and Kurki-Suonio2013). The final step necessary to formulate our problem, the transformation of the RR force, was given recently in Hirvijoki et al. (Reference Hirvijoki, Decker, Brizard and Embreus2015).
$\boldsymbol{v}\times \boldsymbol{B}$
term, the particle phase-space kinetic equation in a magnetized plasma includes the rapid gyro-motion time scale which is often not interesting and is expensive to resolve computationally. It can, however, be eliminated using guiding-centre Lie-transform perturbation methods. The transformation of the Hamiltonian equations of motion is one of the classical results in modern plasma physics (see Littlejohn Reference Littlejohn1983; Cary & Brizard Reference Cary and Brizard2009), and the Fokker–Planck collision operator has been considered in Brizard (Reference Brizard2004), Decker et al. (Reference Decker, Peysson, Brizard and Duthoit2010) and Hirvijoki et al. (Reference Hirvijoki, Brizard, Snicker and Kurki-Suonio2013). The final step necessary to formulate our problem, the transformation of the RR force, was given recently in Hirvijoki et al. (Reference Hirvijoki, Decker, Brizard and Embreus2015).
After the transformation, the guiding-centre kinetic equation for a gyro-angle averaged distribution function
![]() $\langle F_{a}\rangle$
, including Hamiltonian motion in electromagnetic fields, the RR force and Coulomb collisions in the Fokker–Planck limit, is given by
$\langle F_{a}\rangle$
, including Hamiltonian motion in electromagnetic fields, the RR force and Coulomb collisions in the Fokker–Planck limit, is given by
where the
![]() $Z^{{\it\alpha}}$
form the 5D guiding-centre phase space,
$Z^{{\it\alpha}}$
form the 5D guiding-centre phase space,
![]() $\mathscr{J}$
is the guiding-centre phase-space Jacobian,
$\mathscr{J}$
is the guiding-centre phase-space Jacobian,
![]() ${\dot{Z}}^{{\it\alpha}}$
are the Hamiltonian guiding-centre equations of motion and
${\dot{Z}}^{{\it\alpha}}$
are the Hamiltonian guiding-centre equations of motion and
![]() $\langle \mathscr{F}_{gcRR}^{{\it\alpha}}\rangle$
is the contribution from the RR force to the guiding-centre motion. Similarly to the particle phase-space operator in (2.2), we can write the guiding-centre Fokker–Planck collision operator in phase-space divergence form,
$\langle \mathscr{F}_{gcRR}^{{\it\alpha}}\rangle$
is the contribution from the RR force to the guiding-centre motion. Similarly to the particle phase-space operator in (2.2), we can write the guiding-centre Fokker–Planck collision operator in phase-space divergence form,
where
![]() $\langle \mathscr{K}_{ab,gc}^{{\it\alpha}}\rangle$
and
$\langle \mathscr{K}_{ab,gc}^{{\it\alpha}}\rangle$
and
![]() $\langle \mathscr{D}_{ab,gc}^{{\it\alpha}{\it\beta}}\rangle$
are the guiding-centre Coulomb friction and diffusion coefficients.
$\langle \mathscr{D}_{ab,gc}^{{\it\alpha}{\it\beta}}\rangle$
are the guiding-centre Coulomb friction and diffusion coefficients.
2.2. Equations of motion
We solve (2.6) in a uniform plasma, using 2D guiding-centre velocity space coordinates
![]() $Z^{{\it\alpha}}=(p,{\it\xi})$
, where
$Z^{{\it\alpha}}=(p,{\it\xi})$
, where
![]() $p$
is the absolute value of the guiding-centre momentum,
$p$
is the absolute value of the guiding-centre momentum,
![]() ${\it\xi}=p_{\Vert }/p$
is the pitch angle cosine (
${\it\xi}=p_{\Vert }/p$
is the pitch angle cosine (
![]() $p_{\Vert }$
is the guiding-centre momentum parallel to the magnetic field) and the guiding-centre Jacobian is given by
$p_{\Vert }$
is the guiding-centre momentum parallel to the magnetic field) and the guiding-centre Jacobian is given by
![]() $\mathscr{J}=p^{2}$
. In this case, the guiding-centre equations of motion take the simple forms
$\mathscr{J}=p^{2}$
. In this case, the guiding-centre equations of motion take the simple forms
with
![]() $r=q^{2}/(4{\rm\pi}{\it\varepsilon}_{0}mc^{2})$
the classical electron radius and
$r=q^{2}/(4{\rm\pi}{\it\varepsilon}_{0}mc^{2})$
the classical electron radius and
![]() ${\it\Omega}=qB/({\it\gamma}m)$
the gyro-frequency.
${\it\Omega}=qB/({\it\gamma}m)$
the gyro-frequency.
2.3. Collision operator
The particle phase-space friction and diffusion coefficients,
![]() $\boldsymbol{K}_{ab}[\,f_{b}]$
and
$\boldsymbol{K}_{ab}[\,f_{b}]$
and
![]() $\unicode[STIX]{x1D63F}_{ab}[\,f_{b}]$
, are expressed in terms of the five relativistic Braams–Karney potential functions, which are weighted integrals of the background distribution functions
$\unicode[STIX]{x1D63F}_{ab}[\,f_{b}]$
, are expressed in terms of the five relativistic Braams–Karney potential functions, which are weighted integrals of the background distribution functions
![]() $f_{b}$
(see Braams & Karney Reference Braams and Karney1989 and appendix A for details). If the particle species
$f_{b}$
(see Braams & Karney Reference Braams and Karney1989 and appendix A for details). If the particle species
![]() $a$
and
$a$
and
![]() $b$
coincide, the self-collisions result in a nonlinear collision operator. In the present study, the particle phase-space collision operator is transformed into the guiding-centre phase space and linearized around a Maxwellian. The integral terms of the linearized collision operator are neglected and only the test particle contribution is considered. This choice, with some further simplifications, allows analytical solution of (2.6), which will be discussed in § 3.
$b$
coincide, the self-collisions result in a nonlinear collision operator. In the present study, the particle phase-space collision operator is transformed into the guiding-centre phase space and linearized around a Maxwellian. The integral terms of the linearized collision operator are neglected and only the test particle contribution is considered. This choice, with some further simplifications, allows analytical solution of (2.6), which will be discussed in § 3.
The guiding-centre friction and diffusion coefficients
![]() $\langle \mathscr{K}_{ab,gc}^{{\it\alpha}}\rangle$
and
$\langle \mathscr{K}_{ab,gc}^{{\it\alpha}}\rangle$
and
![]() $\langle \mathscr{D}_{ab,gc}^{{\it\alpha}{\it\beta}}\rangle$
that appear in the guiding-centre Fokker–Planck operator in (2.7) are gyro-averaged projections of their guiding-centre pushed-forward particle phase-space counterparts. For a detailed definition of the guiding-centre friction and diffusion coefficients, we refer to Brizard (Reference Brizard2004), Decker et al. (Reference Decker, Peysson, Brizard and Duthoit2010) and Hirvijoki et al. (Reference Hirvijoki, Brizard, Snicker and Kurki-Suonio2013). The general expressions are non-trivial but, in the limit of a uniform plasma, the test-particle operator assuming isotropic background particle distributions becomes diagonal with reasonably simple non-zero components
$\langle \mathscr{D}_{ab,gc}^{{\it\alpha}{\it\beta}}\rangle$
that appear in the guiding-centre Fokker–Planck operator in (2.7) are gyro-averaged projections of their guiding-centre pushed-forward particle phase-space counterparts. For a detailed definition of the guiding-centre friction and diffusion coefficients, we refer to Brizard (Reference Brizard2004), Decker et al. (Reference Decker, Peysson, Brizard and Duthoit2010) and Hirvijoki et al. (Reference Hirvijoki, Brizard, Snicker and Kurki-Suonio2013). The general expressions are non-trivial but, in the limit of a uniform plasma, the test-particle operator assuming isotropic background particle distributions becomes diagonal with reasonably simple non-zero components
where the first term with momentum derivatives is responsible for the slowing down of fast particles and momentum diffusion, while the second term describes scattering in pitch angle.
2.4. Final expression
For the rest of the paper, to streamline notation, we shall suppress the brackets that denote the gyro-averaging and the sub-index from the expression for the parallel electric field. We will also drop the particle species indices as we sum over all the background species in the collision operator. Thus, we will have
![]() ${\it\nu}_{l}=\sum _{b}{\it\nu}_{l,ab}$
,
${\it\nu}_{l}=\sum _{b}{\it\nu}_{l,ab}$
,
![]() $D_{l}=\sum _{b}D_{l,ab}$
and
$D_{l}=\sum _{b}D_{l,ab}$
and
![]() $D_{t}=\sum _{b}D_{t,ab}$
, and our kinetic equation in the continuity form becomes
$D_{t}=\sum _{b}D_{t,ab}$
, and our kinetic equation in the continuity form becomes
 $$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \frac{\partial F}{\partial t}+\frac{1}{p^{2}}\frac{\partial }{\partial p}\left[p^{2}\left(qE{\it\xi}-\frac{{\it\gamma}p(1-{\it\xi}^{2})}{{\it\tau}_{r}}-{\it\nu}_{l}p\right)F-p^{2}D_{l}\frac{\partial F}{\partial p}\right]\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\frac{\partial }{\partial {\it\xi}}\left[(1-{\it\xi}^{2})\left(\frac{qE}{p}F+\frac{{\it\xi}}{{\it\gamma}{\it\tau}_{r}}F-\frac{D_{t}}{p^{2}}\frac{\partial F}{\partial {\it\xi}}\right)\right]=0.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \frac{\partial F}{\partial t}+\frac{1}{p^{2}}\frac{\partial }{\partial p}\left[p^{2}\left(qE{\it\xi}-\frac{{\it\gamma}p(1-{\it\xi}^{2})}{{\it\tau}_{r}}-{\it\nu}_{l}p\right)F-p^{2}D_{l}\frac{\partial F}{\partial p}\right]\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\frac{\partial }{\partial {\it\xi}}\left[(1-{\it\xi}^{2})\left(\frac{qE}{p}F+\frac{{\it\xi}}{{\it\gamma}{\it\tau}_{r}}F-\frac{D_{t}}{p^{2}}\frac{\partial F}{\partial {\it\xi}}\right)\right]=0.\end{eqnarray}$$
In the following, we analyse this equation in detail. We describe the formation of a bump-on-tail in the electron distribution function both analytically and numerically. We also study the threshold conditions for the bump formation and the minimum energy of the bump location.
3. Characteristics of a bump-on-tail feature
The RR force in a straight magnetic field system increases with the square of the perpendicular momentum,
![]() $s_{\bot }^{2}=s^{2}(1-{\it\xi}^{2})$
. As a consequence, the extent of the distribution function will, qualitatively, be limited in
$s_{\bot }^{2}=s^{2}(1-{\it\xi}^{2})$
. As a consequence, the extent of the distribution function will, qualitatively, be limited in
![]() $s_{\bot }$
to a region where the parallel component of the total force acting on an electron is positive. Electrons with higher perpendicular momenta are decelerated since the radiation reaction force overcomes the acceleration due to the parallel electric field. Compared with the case without the RR force, where the distribution function is continuously expanding in
$s_{\bot }$
to a region where the parallel component of the total force acting on an electron is positive. Electrons with higher perpendicular momenta are decelerated since the radiation reaction force overcomes the acceleration due to the parallel electric field. Compared with the case without the RR force, where the distribution function is continuously expanding in
![]() $s_{\bot }$
for increasing values of the parallel momentum
$s_{\bot }$
for increasing values of the parallel momentum
![]() $s_{\Vert }={\it\xi}s$
, the limited extent of the distribution in
$s_{\Vert }={\it\xi}s$
, the limited extent of the distribution in
![]() $s_{\bot }$
when the RR force is included leads to qualitatively different dynamics.
$s_{\bot }$
when the RR force is included leads to qualitatively different dynamics.
The width of the distribution in
![]() $s_{\bot }$
is approximately constant, which means that pitch angle scattering is increasingly more effective at higher
$s_{\bot }$
is approximately constant, which means that pitch angle scattering is increasingly more effective at higher
![]() $s_{\Vert }$
in moving the electrons to the region of phase space where they are decelerated. A consequence of this is that a true steady-state solution of the kinetic equation exists and the distribution function decays exponentially in the far tail, something that was also observed in previous works, such as Andersson et al. (Reference Andersson, Helander and Eriksson2001). Another new feature is the possibility of non-monotonic behaviour in the tail of the steady-state distribution function. It should be noted that this feature cannot be correctly described if the RR force is not implemented in the phase-space divergence form that conserves the phase-space density. Therefore, it is overlooked by some earlier studies. To understand the properties of the bump, and its formation, we will start the following analysis by assuming that a bump exists in the runaway tail, and make assumptions regarding its properties. These assumptions will be justified a posteriori when our results are compared with numerical results in § 4. For further numerical results and insights into the dynamics of the bump, including its temporal development, we refer the reader to Decker et al. (Reference Decker, Hirvijoki, Embréus, Peysson, Stahl, Fülöp and Pusztai2015).
$s_{\Vert }$
in moving the electrons to the region of phase space where they are decelerated. A consequence of this is that a true steady-state solution of the kinetic equation exists and the distribution function decays exponentially in the far tail, something that was also observed in previous works, such as Andersson et al. (Reference Andersson, Helander and Eriksson2001). Another new feature is the possibility of non-monotonic behaviour in the tail of the steady-state distribution function. It should be noted that this feature cannot be correctly described if the RR force is not implemented in the phase-space divergence form that conserves the phase-space density. Therefore, it is overlooked by some earlier studies. To understand the properties of the bump, and its formation, we will start the following analysis by assuming that a bump exists in the runaway tail, and make assumptions regarding its properties. These assumptions will be justified a posteriori when our results are compared with numerical results in § 4. For further numerical results and insights into the dynamics of the bump, including its temporal development, we refer the reader to Decker et al. (Reference Decker, Hirvijoki, Embréus, Peysson, Stahl, Fülöp and Pusztai2015).
Considering a possible bump-on-tail scenario, we study (2.20) in a region where the electrons have high velocities compared with the electron and ion thermal speeds,
![]() $v\gg v_{th,e},v_{th,i}$
. Then, the slowing-down force is dominated by electron–electron collisions and it overshadows momentum diffusion. For pitch angle scattering, collisions with both ions and the electron bulk are important.
$v\gg v_{th,e},v_{th,i}$
. Then, the slowing-down force is dominated by electron–electron collisions and it overshadows momentum diffusion. For pitch angle scattering, collisions with both ions and the electron bulk are important.
In the limit where the bulk populations are non-relativistic Maxwellians, we have for the friction coefficient at high speeds
and similarly for the transverse diffusion coefficient
where
![]() $E_{c}$
is the critical electric field (1.1),
$E_{c}$
is the critical electric field (1.1),
![]() $Z_{eff}$
is the effective ion charge and
$Z_{eff}$
is the effective ion charge and
![]() ${\it\beta}=v/c$
. These estimates coincide with the expressions in Andersson et al. (Reference Andersson, Helander and Eriksson2001). We define the normalized momentum
${\it\beta}=v/c$
. These estimates coincide with the expressions in Andersson et al. (Reference Andersson, Helander and Eriksson2001). We define the normalized momentum
![]() $s=p/(m_{e}c)$
, time
$s=p/(m_{e}c)$
, time
![]() ${\it\tau}=eE_{c}t/(m_{e}c)$
, radiation reaction time scale
${\it\tau}=eE_{c}t/(m_{e}c)$
, radiation reaction time scale
![]() ${\it\sigma}^{-1}=eE_{c}{\it\tau}_{r}/(m_{e}c)$
and electric field
${\it\sigma}^{-1}=eE_{c}{\it\tau}_{r}/(m_{e}c)$
and electric field
![]() $\hat{E}=-E/E_{c}$
, and transform the kinetic equation into a dimensionless form for further analysis,
$\hat{E}=-E/E_{c}$
, and transform the kinetic equation into a dimensionless form for further analysis,
 $$\begin{eqnarray}\displaystyle & & \displaystyle \frac{\partial F}{\partial {\it\tau}}+\frac{1}{s^{2}}\frac{\partial }{\partial s}\left[s^{2}\left(\hat{E}{\it\xi}-{\it\sigma}{\it\gamma}s(1-{\it\xi}^{2})-\frac{{\it\gamma}^{2}}{s^{2}}\right)F\right]\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\frac{\partial }{\partial {\it\xi}}\left[(1-{\it\xi}^{2})\left(\hat{E}\frac{F}{s}+\frac{{\it\sigma}{\it\xi}}{{\it\gamma}}F-\frac{{\it\gamma}}{s}\frac{1+Z_{eff}}{2s^{2}}\frac{\partial F}{\partial {\it\xi}}\right)\right]=0.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \frac{\partial F}{\partial {\it\tau}}+\frac{1}{s^{2}}\frac{\partial }{\partial s}\left[s^{2}\left(\hat{E}{\it\xi}-{\it\sigma}{\it\gamma}s(1-{\it\xi}^{2})-\frac{{\it\gamma}^{2}}{s^{2}}\right)F\right]\nonumber\\ \displaystyle & & \displaystyle \qquad +\,\frac{\partial }{\partial {\it\xi}}\left[(1-{\it\xi}^{2})\left(\hat{E}\frac{F}{s}+\frac{{\it\sigma}{\it\xi}}{{\it\gamma}}F-\frac{{\it\gamma}}{s}\frac{1+Z_{eff}}{2s^{2}}\frac{\partial F}{\partial {\it\xi}}\right)\right]=0.\end{eqnarray}$$
As the electric field affects only the parallel acceleration we expect the system to be strongly biased about
![]() ${\it\xi}=1$
. The phase-space volume element in
${\it\xi}=1$
. The phase-space volume element in
![]() $(s,{\it\xi})$
coordinates (
$(s,{\it\xi})$
coordinates (
![]() $\mathscr{J}\sim s^{2}$
), however, scales nonlinearly close to
$\mathscr{J}\sim s^{2}$
), however, scales nonlinearly close to
![]() ${\it\xi}\approx 1$
. A better choice for further studies close to the
${\it\xi}\approx 1$
. A better choice for further studies close to the
![]() ${\it\xi}=1$
region is to use coordinates
${\it\xi}=1$
region is to use coordinates
![]() $(s_{\Vert },s_{\bot })$
that have a Jacobian
$(s_{\Vert },s_{\bot })$
that have a Jacobian
![]() $\mathscr{J}\sim s_{\bot }$
that stays constant with respect to
$\mathscr{J}\sim s_{\bot }$
that stays constant with respect to
![]() $s_{\Vert }$
. The new coordinates relate to
$s_{\Vert }$
. The new coordinates relate to
![]() $(s,{\it\xi})$
according to
$(s,{\it\xi})$
according to
 $$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \frac{\partial F}{\partial {\it\tau}}+\hat{E}\frac{\partial F}{\partial s_{\Vert }}-\frac{2F}{s}-\frac{{\it\gamma}^{2}}{s^{2}}\left(\frac{s_{\Vert }}{s}\frac{\partial F}{\partial s_{\Vert }}+\frac{s_{\bot }}{s}\frac{\partial F}{\partial s_{\bot }}\right)\nonumber\\ \displaystyle & & \displaystyle \qquad \quad -\,\frac{{\it\gamma}(1+Z_{eff})}{2s}\left[\frac{1}{s_{\bot }}\frac{\partial }{\partial s_{\bot }}\left(s_{\bot }\frac{\partial F}{\partial s_{\bot }}\right)+\frac{s_{\bot }^{2}}{s^{2}}\left(\frac{\partial ^{2}F}{\partial s_{\Vert }^{2}}-\frac{\partial ^{2}F}{\partial s_{\bot }^{2}}\right)\right.\nonumber\\ \displaystyle & & \displaystyle \left.\qquad \quad -\,2\frac{s_{\Vert }s_{\bot }}{s^{2}}\frac{\partial ^{2}F}{\partial s_{\Vert }\partial s_{\bot }}-2\frac{s_{\Vert }}{s^{2}}\left(\frac{\partial F}{\partial s_{\Vert }}+\frac{s_{\bot }}{s_{\Vert }}\frac{\partial F}{\partial s_{\bot }}\right)\right]\nonumber\\ \displaystyle & & \displaystyle \qquad \quad -\,\frac{{\it\sigma}}{{\it\gamma}}\left[(2+4s_{\bot }^{2})F+s_{\bot }(1+s_{\bot }^{2})\frac{\partial F}{\partial s_{\bot }}+s_{\Vert }s_{\bot }^{2}\frac{\partial F}{\partial s_{\Vert }}\right]=0.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \frac{\partial F}{\partial {\it\tau}}+\hat{E}\frac{\partial F}{\partial s_{\Vert }}-\frac{2F}{s}-\frac{{\it\gamma}^{2}}{s^{2}}\left(\frac{s_{\Vert }}{s}\frac{\partial F}{\partial s_{\Vert }}+\frac{s_{\bot }}{s}\frac{\partial F}{\partial s_{\bot }}\right)\nonumber\\ \displaystyle & & \displaystyle \qquad \quad -\,\frac{{\it\gamma}(1+Z_{eff})}{2s}\left[\frac{1}{s_{\bot }}\frac{\partial }{\partial s_{\bot }}\left(s_{\bot }\frac{\partial F}{\partial s_{\bot }}\right)+\frac{s_{\bot }^{2}}{s^{2}}\left(\frac{\partial ^{2}F}{\partial s_{\Vert }^{2}}-\frac{\partial ^{2}F}{\partial s_{\bot }^{2}}\right)\right.\nonumber\\ \displaystyle & & \displaystyle \left.\qquad \quad -\,2\frac{s_{\Vert }s_{\bot }}{s^{2}}\frac{\partial ^{2}F}{\partial s_{\Vert }\partial s_{\bot }}-2\frac{s_{\Vert }}{s^{2}}\left(\frac{\partial F}{\partial s_{\Vert }}+\frac{s_{\bot }}{s_{\Vert }}\frac{\partial F}{\partial s_{\bot }}\right)\right]\nonumber\\ \displaystyle & & \displaystyle \qquad \quad -\,\frac{{\it\sigma}}{{\it\gamma}}\left[(2+4s_{\bot }^{2})F+s_{\bot }(1+s_{\bot }^{2})\frac{\partial F}{\partial s_{\bot }}+s_{\Vert }s_{\bot }^{2}\frac{\partial F}{\partial s_{\Vert }}\right]=0.\end{eqnarray}$$
Instead of attempting to solve (3.6), in the following we will concentrate on the dynamics at
![]() $s_{\bot }=0$
, which will be sufficient to prove the existence of a bump and to estimate its location in the electron tail.
$s_{\bot }=0$
, which will be sufficient to prove the existence of a bump and to estimate its location in the electron tail.
We assume the distribution to be a smooth function of
![]() $s_{\bot }$
, which allows us to create a power series expansion around
$s_{\bot }$
, which allows us to create a power series expansion around
![]() $s_{\bot }=0$
:
$s_{\bot }=0$
:
Because the electric field is acting only in the parallel direction,
![]() $F$
is ‘even’ in
$F$
is ‘even’ in
![]() $s_{\bot }$
, i.e. we can formally state that
$s_{\bot }$
, i.e. we can formally state that
![]() $F(s_{\Vert },s_{\bot })=F(s_{\Vert },-s_{\bot })$
although our phase space does not extend to
$F(s_{\Vert },s_{\bot })=F(s_{\Vert },-s_{\bot })$
although our phase space does not extend to
![]() $s_{\bot }<0$
. Thus, all the odd
$s_{\bot }<0$
. Thus, all the odd
![]() $s_{\bot }$
derivatives at
$s_{\bot }$
derivatives at
![]() $s_{\bot }=0$
must vanish, and we find
$s_{\bot }=0$
must vanish, and we find
With the help of the expansion, we may accurately calculate the limit
and write the
![]() $s_{\bot }=0$
limit of the kinetic equation as
$s_{\bot }=0$
limit of the kinetic equation as
 $$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \left[\frac{\partial F}{\partial {\it\tau}}\right]_{(s_{\Vert },0)}+\left(\hat{E}-\frac{1+s_{\Vert }^{2}}{s_{\Vert }^{2}}+\frac{(1+Z_{eff})\sqrt{1+s_{\Vert }^{2}}}{s_{\Vert }^{2}}\right)\left[\frac{\partial F}{\partial s_{\Vert }}\right]_{(s_{\Vert },0)}\nonumber\\ \displaystyle & & \displaystyle \quad -\,\frac{(1+Z_{eff})\sqrt{1+s_{\Vert }^{2}}}{s_{\Vert }}\left[\frac{\partial ^{2}F}{\partial s_{\bot }^{2}}\right]_{(s_{\Vert },0)}-2\left(\frac{{\it\sigma}}{\sqrt{1+s_{\Vert }^{2}}}+\frac{1}{s_{\Vert }}\right)[F]_{(s_{\Vert },0)}=0.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \displaystyle \left[\frac{\partial F}{\partial {\it\tau}}\right]_{(s_{\Vert },0)}+\left(\hat{E}-\frac{1+s_{\Vert }^{2}}{s_{\Vert }^{2}}+\frac{(1+Z_{eff})\sqrt{1+s_{\Vert }^{2}}}{s_{\Vert }^{2}}\right)\left[\frac{\partial F}{\partial s_{\Vert }}\right]_{(s_{\Vert },0)}\nonumber\\ \displaystyle & & \displaystyle \quad -\,\frac{(1+Z_{eff})\sqrt{1+s_{\Vert }^{2}}}{s_{\Vert }}\left[\frac{\partial ^{2}F}{\partial s_{\bot }^{2}}\right]_{(s_{\Vert },0)}-2\left(\frac{{\it\sigma}}{\sqrt{1+s_{\Vert }^{2}}}+\frac{1}{s_{\Vert }}\right)[F]_{(s_{\Vert },0)}=0.\end{eqnarray}$$
Assuming that a steady-state solution exists, the possible extrema are characterized by the condition
We thus find an algebraic equation that defines the locations of these extrema:
 $$\begin{eqnarray}2\left(\frac{{\it\sigma}}{\sqrt{1+s_{\Vert }^{2}}}+\frac{1}{s_{\Vert }}\right)+\frac{(1+Z_{eff})\sqrt{1+s_{\Vert }^{2}}}{s_{\Vert }}\left[\frac{1}{F}\frac{\partial ^{2}F}{\partial s_{\bot }^{2}}\right]_{(s_{\Vert },0)}=0.\end{eqnarray}$$
$$\begin{eqnarray}2\left(\frac{{\it\sigma}}{\sqrt{1+s_{\Vert }^{2}}}+\frac{1}{s_{\Vert }}\right)+\frac{(1+Z_{eff})\sqrt{1+s_{\Vert }^{2}}}{s_{\Vert }}\left[\frac{1}{F}\frac{\partial ^{2}F}{\partial s_{\bot }^{2}}\right]_{(s_{\Vert },0)}=0.\end{eqnarray}$$
3.1. Threshold condition for the appearance of the bump
Considering a steady-state solution to (3.10), in a situation where the bump is on the verge of appearing, a single inflection point exists in the distribution function instead of local maxima or minima. In this section we derive a threshold condition describing the appearance of an inflection point, by requiring the first and second
![]() $s_{\Vert }$
derivatives of the distribution to vanish simultaneously.
$s_{\Vert }$
derivatives of the distribution to vanish simultaneously.
Before we start the analysis, we note that the steady-state distribution function represented by equation (12) of Andersson et al. (Reference Andersson, Helander and Eriksson2001) is separable in
![]() $s_{\Vert }$
and
$s_{\Vert }$
and
![]() $s_{\bot }$
, and it is of the form
$s_{\bot }$
, and it is of the form
![]() $\propto \text{exp}[-W_{\infty }^{2}s_{\bot }^{2}/2]$
, where
$\propto \text{exp}[-W_{\infty }^{2}s_{\bot }^{2}/2]$
, where
![]() $W_{\infty }^{2}=2{\it\sigma}/(\hat{E}-1)$
. To find this result they neglect
$W_{\infty }^{2}=2{\it\sigma}/(\hat{E}-1)$
. To find this result they neglect
![]() $f/s_{\Vert }$
corrections compared with
$f/s_{\Vert }$
corrections compared with
![]() $\partial f/\partial s_{\Vert }$
terms in the kinetic equation, which is appropriate in the very far tail (
$\partial f/\partial s_{\Vert }$
terms in the kinetic equation, which is appropriate in the very far tail (
![]() $s_{\Vert }$
corresponds to
$s_{\Vert }$
corresponds to
![]() $p_{\Vert }$
in the notation of Andersson et al.
Reference Andersson, Helander and Eriksson2001). Therefore, the quantity
$p_{\Vert }$
in the notation of Andersson et al.
Reference Andersson, Helander and Eriksson2001). Therefore, the quantity
should approach
![]() $W_{\infty }^{2}$
in the
$W_{\infty }^{2}$
in the
![]() $s_{\Vert }\rightarrow \infty$
limit. Thus, it is useful to define
$s_{\Vert }\rightarrow \infty$
limit. Thus, it is useful to define
![]() ${\it\kappa}(s_{\Vert })$
, so that
${\it\kappa}(s_{\Vert })$
, so that
![]() $W^{2}(s_{\Vert })={\it\kappa}(s_{\Vert })W_{\infty }^{2}$
and
$W^{2}(s_{\Vert })={\it\kappa}(s_{\Vert })W_{\infty }^{2}$
and
![]() ${\it\kappa}\rightarrow 1$
as
${\it\kappa}\rightarrow 1$
as
![]() $s_{\Vert }\rightarrow \infty$
. Numerical calculations tell us that
$s_{\Vert }\rightarrow \infty$
. Numerical calculations tell us that
![]() $0<{\it\kappa}\leqslant 1$
for the regions of interest in the runaway tail, and
$0<{\it\kappa}\leqslant 1$
for the regions of interest in the runaway tail, and
![]() ${\it\kappa}$
is often a slowly varying function of
${\it\kappa}$
is often a slowly varying function of
![]() $s_{\Vert }$
. That is, the characteristic width of the distribution function in the
$s_{\Vert }$
. That is, the characteristic width of the distribution function in the
![]() $s_{\bot }$
direction,
$s_{\bot }$
direction,
![]() $1/W^{2}$
, decreases with increasing
$1/W^{2}$
, decreases with increasing
![]() $s_{\Vert }$
, and slowly asymptotes to a constant value. For now, we may simply use
$s_{\Vert }$
, and slowly asymptotes to a constant value. For now, we may simply use
![]() $0<{\it\kappa}\leqslant 1$
as a working hypothesis to be verified through numerical calculations later.
$0<{\it\kappa}\leqslant 1$
as a working hypothesis to be verified through numerical calculations later.
We start with (3.12) satisfied at extrema or inflection of the distribution function and rewrite it as
where
![]() $K(s_{\Vert })=W_{\infty }^{2}(1+Z_{eff}){\it\kappa}(s_{\Vert })=\bar{E}^{-1}{\it\sigma}{\it\kappa}(s_{\Vert })$
with
$K(s_{\Vert })=W_{\infty }^{2}(1+Z_{eff}){\it\kappa}(s_{\Vert })=\bar{E}^{-1}{\it\sigma}{\it\kappa}(s_{\Vert })$
with
![]() $\bar{E}=(\hat{E}-1)/[2(1+Z_{eff})]$
. It is useful to form
$\bar{E}=(\hat{E}-1)/[2(1+Z_{eff})]$
. It is useful to form
where the prime denotes a derivative with respect to
![]() $s_{\Vert }$
, and we neglected a term,
$s_{\Vert }$
, and we neglected a term,
![]() $-K^{\prime }(s_{\Vert })(1+s_{\Vert }^{2})/2$
, assuming
$-K^{\prime }(s_{\Vert })(1+s_{\Vert }^{2})/2$
, assuming
![]() ${\it\kappa}$
to be a sufficiently slowly varying function of
${\it\kappa}$
to be a sufficiently slowly varying function of
![]() $s_{\Vert }$
. From (3.15) we see that
$s_{\Vert }$
. From (3.15) we see that
![]() $L^{\prime }(s_{\Vert })\rightarrow -\infty$
as
$L^{\prime }(s_{\Vert })\rightarrow -\infty$
as
![]() $s_{\Vert }\rightarrow \infty$
, while
$s_{\Vert }\rightarrow \infty$
, while
![]() $L^{\prime }|_{s_{\Vert }=0}=2{\it\sigma}>0$
. It can also be shown that
$L^{\prime }|_{s_{\Vert }=0}=2{\it\sigma}>0$
. It can also be shown that
![]() $L^{\prime }=0$
only has one root for positive values of
$L^{\prime }=0$
only has one root for positive values of
![]() $s_{\Vert }$
, which then has to correspond to a single maximum of
$s_{\Vert }$
, which then has to correspond to a single maximum of
![]() $L$
.
$L$
.
If the distribution has an inflection point, both
![]() $L$
and
$L$
and
![]() $L^{\prime }$
should vanish there. Assuming the slowly varying
$L^{\prime }$
should vanish there. Assuming the slowly varying
![]() ${\it\kappa}$
to be a constant, the system of (3.14) and (3.15) can be solved for
${\it\kappa}$
to be a constant, the system of (3.14) and (3.15) can be solved for
![]() $s_{\Vert }$
and
$s_{\Vert }$
and
![]() $K$
to find
$K$
to find
 $$\begin{eqnarray}\displaystyle K_{0}\equiv K(s_{\Vert 0}) & = & \displaystyle (4\sqrt{2}{\it\sigma})^{-1}\left[8{\it\sigma}\sqrt{4-\frac{8}{3+\sqrt{1+8{\it\sigma}^{2}}}}\right.\nonumber\\ \displaystyle & & \displaystyle +\,\left.\left(1+4{\it\sigma}^{2}-\sqrt{1+8{\it\sigma}^{2}}\right)\sqrt{2-\frac{8}{3+\sqrt{1+8{\it\sigma}^{2}}}}\right]\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle K_{0}\equiv K(s_{\Vert 0}) & = & \displaystyle (4\sqrt{2}{\it\sigma})^{-1}\left[8{\it\sigma}\sqrt{4-\frac{8}{3+\sqrt{1+8{\it\sigma}^{2}}}}\right.\nonumber\\ \displaystyle & & \displaystyle +\,\left.\left(1+4{\it\sigma}^{2}-\sqrt{1+8{\it\sigma}^{2}}\right)\sqrt{2-\frac{8}{3+\sqrt{1+8{\it\sigma}^{2}}}}\right]\end{eqnarray}$$
and
where the subscript 0 refers to values of quantities at the threshold of the bump appearance. By inspecting the expressions (3.16) and (3.17) we find that both of them increase with
![]() ${\it\sigma}$
monotonically;
${\it\sigma}$
monotonically;
![]() $K_{0}$
between 2 and
$K_{0}$
between 2 and
![]() $\infty$
, and
$\infty$
, and
![]() $s_{\Vert 0}$
between 0 and 1. This means that an inflection point is always located below
$s_{\Vert 0}$
between 0 and 1. This means that an inflection point is always located below
![]() $s_{\Vert }=1$
. Note, that we assume the inflection point to be sufficiently far from the bulk, and that
$s_{\Vert }=1$
. Note, that we assume the inflection point to be sufficiently far from the bulk, and that
![]() ${\it\kappa}^{\prime }$
is small; violation of these assumptions may move
${\it\kappa}^{\prime }$
is small; violation of these assumptions may move
![]() $s_{\Vert 0}$
above unity. However, since this problem cannot be addressed until the more complete (2.20) is solved, we assume that the conditions above are fulfilled in order to proceed analytically. Since
$s_{\Vert 0}$
above unity. However, since this problem cannot be addressed until the more complete (2.20) is solved, we assume that the conditions above are fulfilled in order to proceed analytically. Since
![]() $s_{\Vert }<1$
, we can make use of the expansion
$s_{\Vert }<1$
, we can make use of the expansion
By neglecting
![]() $O(s_{\Vert }^{4})$
terms (which is a reasonably good approximation even when
$O(s_{\Vert }^{4})$
terms (which is a reasonably good approximation even when
![]() $s_{\Vert }$
approaches unity), (3.14) becomes quadratic in
$s_{\Vert }$
approaches unity), (3.14) becomes quadratic in
![]() $s_{\Vert }$
:
$s_{\Vert }$
:
At the inflection point
![]() $s_{\Vert 0}$
, (3.19) must have a single root, which requires the discriminant to vanish. This determines the threshold value of
$s_{\Vert 0}$
, (3.19) must have a single root, which requires the discriminant to vanish. This determines the threshold value of
![]() $K$
:
$K$
:
which is positive. This can be substituted back into (3.19) to find
Combination of
![]() $K(s_{\Vert })=\bar{E}^{-1}{\it\sigma}{\it\kappa}(s_{\Vert })$
with (3.20) to solve for a positive
$K(s_{\Vert })=\bar{E}^{-1}{\it\sigma}{\it\kappa}(s_{\Vert })$
with (3.20) to solve for a positive
![]() ${\it\sigma}$
that corresponds to
${\it\sigma}$
that corresponds to
![]() $K\geqslant 2$
yields
$K\geqslant 2$
yields
![]() ${\it\sigma}$
as a function of
${\it\sigma}$
as a function of
![]() $\bar{E}$
at the threshold for bump formation:
$\bar{E}$
at the threshold for bump formation:
where
![]() ${\it\kappa}={\it\kappa}(s_{\Vert }=s_{\Vert 0})\leqslant 1$
is treated as a parameter. When
${\it\kappa}={\it\kappa}(s_{\Vert }=s_{\Vert 0})\leqslant 1$
is treated as a parameter. When
![]() ${\it\sigma}$
is increased above
${\it\sigma}$
is increased above
![]() ${\it\sigma}_{0}$
,
${\it\sigma}_{0}$
,
![]() $L$
becomes negative and no bump appears. Reducing
$L$
becomes negative and no bump appears. Reducing
![]() ${\it\kappa}$
below unity increases the threshold value of
${\it\kappa}$
below unity increases the threshold value of
![]() ${\it\sigma}$
. Thus, (3.22) with
${\it\sigma}$
. Thus, (3.22) with
![]() ${\it\kappa}=1$
represents an absolute lower threshold in
${\it\kappa}=1$
represents an absolute lower threshold in
![]() ${\it\sigma}$
for a monotonic behaviour of the steady-state distribution function. Furthermore, even at
${\it\sigma}$
for a monotonic behaviour of the steady-state distribution function. Furthermore, even at
![]() ${\it\kappa}=1$
the threshold is limited to the region
${\it\kappa}=1$
the threshold is limited to the region
![]() $\bar{E}<1$
; thus a bump should always appear when
$\bar{E}<1$
; thus a bump should always appear when
![]() $\bar{E}\geqslant 1$
.
$\bar{E}\geqslant 1$
.
We have considered
![]() $K(s_{\Vert }=0)>2$
, in which case
$K(s_{\Vert }=0)>2$
, in which case
![]() $L(s_{\Vert })=0$
can have zero (no bump), one (threshold) or two (bump exists) positive real roots. When
$L(s_{\Vert })=0$
can have zero (no bump), one (threshold) or two (bump exists) positive real roots. When
![]() $K(s_{\Vert }=0)<2$
there is only a single positive root of
$K(s_{\Vert }=0)<2$
there is only a single positive root of
![]() $L(s_{\Vert })$
. Since the distribution function cannot have a positive slope in the high-
$L(s_{\Vert })$
. Since the distribution function cannot have a positive slope in the high-
![]() $s_{\Vert }$
limit this root should also correspond to a bump. That, however, requires the existence of a minimum in the distribution function along the positive
$s_{\Vert }$
limit this root should also correspond to a bump. That, however, requires the existence of a minimum in the distribution function along the positive
![]() $s_{\Vert }$
axis, which must then appear outside the domain of validity of (3.12). In fact, this minimum will appear close to the bulk part of the electron distribution, where neglected corrections to the collision operator become important.
$s_{\Vert }$
axis, which must then appear outside the domain of validity of (3.12). In fact, this minimum will appear close to the bulk part of the electron distribution, where neglected corrections to the collision operator become important.
We can conclude that for
![]() $\bar{E}\geqslant 1$
, there should always be a bump in the steady-state distribution function as long as there is a finite magnetic field. This, perhaps somewhat counterintuitive, result needs some clarification to accommodate the well-known
$\bar{E}\geqslant 1$
, there should always be a bump in the steady-state distribution function as long as there is a finite magnetic field. This, perhaps somewhat counterintuitive, result needs some clarification to accommodate the well-known
![]() ${\it\sigma}=0$
limit. When no loss mechanisms are considered (in this case when
${\it\sigma}=0$
limit. When no loss mechanisms are considered (in this case when
![]() ${\it\sigma}=0$
), the electron distribution has no steady-state solution, and the runaway tail at
${\it\sigma}=0$
), the electron distribution has no steady-state solution, and the runaway tail at
![]() $s_{\bot }=0$
should converge to a
$s_{\bot }=0$
should converge to a
![]() $1/s_{\Vert }$
decay. When
$1/s_{\Vert }$
decay. When
![]() ${\it\sigma}$
is small, the bump location moves to high values in
${\it\sigma}$
is small, the bump location moves to high values in
![]() $s_{\Vert }$
, as will be shown in the next section. The runaway tail always builds up starting from the bulk, and, for a tiny
$s_{\Vert }$
, as will be shown in the next section. The runaway tail always builds up starting from the bulk, and, for a tiny
![]() ${\it\sigma}$
, the process may take such a long time that the distribution never becomes non-monotonic in practice. In this scenario the steady-state distribution and the bump have no relevance. Moreover, other loss mechanisms may limit the distribution function to momenta below
${\it\sigma}$
, the process may take such a long time that the distribution never becomes non-monotonic in practice. In this scenario the steady-state distribution and the bump have no relevance. Moreover, other loss mechanisms may limit the distribution function to momenta below
![]() $s_{\Vert 0}$
in realistic cases.
$s_{\Vert 0}$
in realistic cases.
3.2. An estimate for the bump location in the far tail
In order to proceed and estimate the location of the bump and the shape of the distribution function, we look for a steady-state solution in a region where the guiding-centre parallel momentum is large. Using the expansion
(3.10) gives
We neglect the
![]() $O(s_{\Vert }^{-1})$
term, which is valid if
$O(s_{\Vert }^{-1})$
term, which is valid if
![]() $\hat{E}-1$
is not very small, and assume that the width of the distribution function in the
$\hat{E}-1$
is not very small, and assume that the width of the distribution function in the
![]() $s_{\bot }$
direction, and thus
$s_{\bot }$
direction, and thus
![]() $W^{2}=-F^{-1}(\partial ^{2}F/\partial s_{\bot }^{2})|_{(s_{\Vert },0)}$
, stays approximately constant close to the bump. This essentially means that we are looking for a separable solution of the form
$W^{2}=-F^{-1}(\partial ^{2}F/\partial s_{\bot }^{2})|_{(s_{\Vert },0)}$
, stays approximately constant close to the bump. This essentially means that we are looking for a separable solution of the form
![]() $F\sim h(s_{\Vert })g(s_{\bot })$
. We obtain an ordinary differential equation
$F\sim h(s_{\Vert })g(s_{\bot })$
. We obtain an ordinary differential equation
which is solved by
and the location of the bump-on-tail is given by
If we again assume that
![]() ${\it\kappa}$
does not exceed unity, recalling
${\it\kappa}$
does not exceed unity, recalling
![]() $W_{\infty }^{2}=2{\it\sigma}/(\hat{E}-1)$
, we find a lower bound for the parallel momentum at the bump,
$W_{\infty }^{2}=2{\it\sigma}/(\hat{E}-1)$
, we find a lower bound for the parallel momentum at the bump,
We see that for small values of
![]() ${\it\sigma}$
, the bump would appear at high parallel momenta. By setting
${\it\sigma}$
, the bump would appear at high parallel momenta. By setting
![]() $s_{\Vert ,\mathit{min}}$
to some upper limit of physical interest,
$s_{\Vert ,\mathit{min}}$
to some upper limit of physical interest,
![]() $s_{\Vert ,L}$
, (3.28) may be used to find an estimate for a lower ‘practical limit’ in
$s_{\Vert ,L}$
, (3.28) may be used to find an estimate for a lower ‘practical limit’ in
![]() ${\it\sigma}$
for the appearance of the bump. Namely, if
${\it\sigma}$
for the appearance of the bump. Namely, if
![]() ${\it\sigma}$
is smaller than
${\it\sigma}$
is smaller than
for
![]() ${\it\kappa}=1$
, then a bump would only appear at some large parallel momentum above
${\it\kappa}=1$
, then a bump would only appear at some large parallel momentum above
![]() $s_{\Vert ,L}$
, which is then deemed physically irrelevant. It should be noted that if the bump is in the far tail,
$s_{\Vert ,L}$
, which is then deemed physically irrelevant. It should be noted that if the bump is in the far tail,
![]() ${\it\kappa}$
can be significantly less than unity, as will be shown in the next section, using numerical simulations. Letting
${\it\kappa}$
can be significantly less than unity, as will be shown in the next section, using numerical simulations. Letting
![]() ${\it\kappa}<1$
increases the practical limit in
${\it\kappa}<1$
increases the practical limit in
![]() ${\it\sigma}$
. Another implication of (3.29) is that for a normalized electric field higher than
${\it\sigma}$
. Another implication of (3.29) is that for a normalized electric field higher than
![]() $\bar{E}=s_{\Vert ,L}/2$
, the bump always appears above
$\bar{E}=s_{\Vert ,L}/2$
, the bump always appears above
![]() $s_{\Vert ,L}$
for any value of
$s_{\Vert ,L}$
for any value of
![]() ${\it\sigma}$
.
${\it\sigma}$
.
4. Comparison with numerical results
The numerical results shown in this section were performed with the continuum simulation tool CODE used in its time-independent mode. CODE solves the two-dimensional momentum space kinetic equation in a homogeneous plasma, using a linearized Fokker–Planck operator valid for arbitrary electron energies. For a detailed description of the tool, see Landreman et al. (Reference Landreman, Stahl and Fülöp2014).
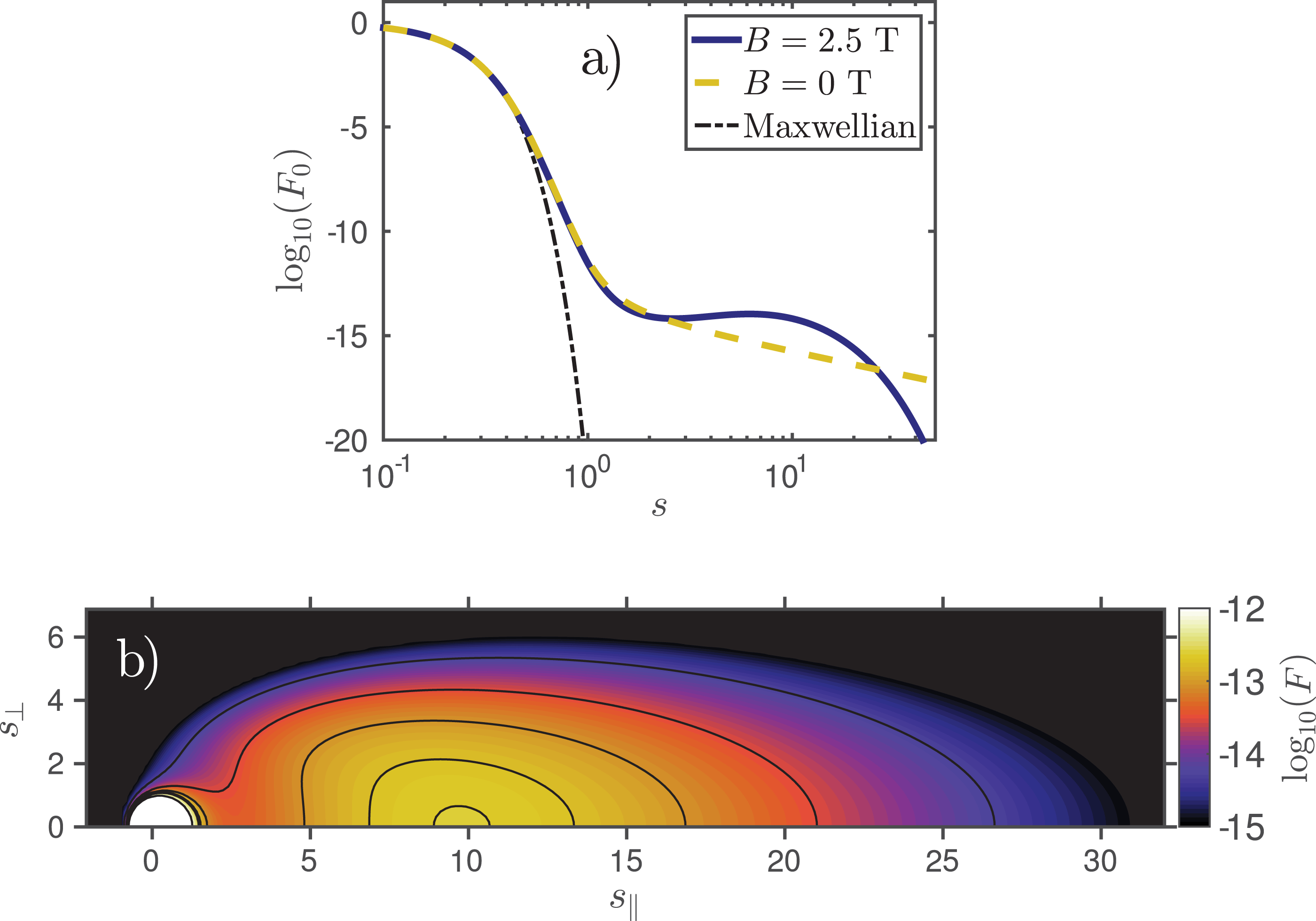
Figure 1. Typical examples of non-monotonic runaway electron distribution functions. (a) The pitch angle average of the distribution function with (solid curve) and without (dashed) synchrotron radiation reaction. A Maxwellian distribution is also indicated (dash-dotted). (b) Contour plot of the distribution function corresponding to the solid curve in (a), as a function of
![]() $s_{\Vert }$
and
$s_{\Vert }$
and
![]() $s_{\bot }$
.
$s_{\bot }$
.
First, we provide a typical example of a non-monotonic runaway distribution function in the presence of radiation reaction. Figure 1(a) shows the momentum dependence of the pitch angle averaged runaway electron distribution with (
![]() $B=2.5~\text{T}$
) and without (
$B=2.5~\text{T}$
) and without (
![]() $B=0~\text{T}$
) radiation reaction force, plotted with solid and dashed curves respectively. Technically, the pitch angle averaged distribution is the lowest mode in a Legendre polynomial expansion of
$B=0~\text{T}$
) radiation reaction force, plotted with solid and dashed curves respectively. Technically, the pitch angle averaged distribution is the lowest mode in a Legendre polynomial expansion of
![]() $F$
in
$F$
in
![]() ${\it\xi}$
, normalized so that
${\it\xi}$
, normalized so that
![]() $F$
is unity at its maximum. The simulations were performed with the parameters
$F$
is unity at its maximum. The simulations were performed with the parameters
![]() $T_{e}=5~\text{keV}$
,
$T_{e}=5~\text{keV}$
,
![]() $n_{e}=2\times 10^{19}~\text{m}^{-3}$
,
$n_{e}=2\times 10^{19}~\text{m}^{-3}$
,
![]() $Z_{eff}=1.2$
and
$Z_{eff}=1.2$
and
![]() $\hat{E}=2$
. It should be noted that the distribution function without radiation reaction represents a quasi-steady state. The lack of loss mechanisms leads to a slow but steady depletion of the bulk electron population, as more and more electrons run away and leave the computational domain. This outflow must be balanced by an artificial source of thermal (Maxwellian) electrons to maintain the quasi-steady state. In the presence of radiation reaction, the distribution is a true steady state. When the radiation reaction is included, the non-monotonic feature is present when the distribution is averaged over pitch angles in the present example. However, we note that for less pronounced bumps, the pitch angle averaged distribution can have a monotonic tail, or it may exhibit a bump at some values of
$\hat{E}=2$
. It should be noted that the distribution function without radiation reaction represents a quasi-steady state. The lack of loss mechanisms leads to a slow but steady depletion of the bulk electron population, as more and more electrons run away and leave the computational domain. This outflow must be balanced by an artificial source of thermal (Maxwellian) electrons to maintain the quasi-steady state. In the presence of radiation reaction, the distribution is a true steady state. When the radiation reaction is included, the non-monotonic feature is present when the distribution is averaged over pitch angles in the present example. However, we note that for less pronounced bumps, the pitch angle averaged distribution can have a monotonic tail, or it may exhibit a bump at some values of
![]() $s$
that are appreciably lower than those where the bump is observed in the full 2D distribution. This may have an impact on the possibility for bump-on-tail-type instabilities to arise. Figure 1(b) shows a contour plot in
$s$
that are appreciably lower than those where the bump is observed in the full 2D distribution. This may have an impact on the possibility for bump-on-tail-type instabilities to arise. Figure 1(b) shows a contour plot in
![]() $s_{\Vert }{-}s_{\bot }$
momentum space of the distribution function corresponding to the solid curve in figure 1(a). Although this example is representative of a typical runaway electron distribution, the location and height of the bump, and the width of the distribution in
$s_{\Vert }{-}s_{\bot }$
momentum space of the distribution function corresponding to the solid curve in figure 1(a). Although this example is representative of a typical runaway electron distribution, the location and height of the bump, and the width of the distribution in
![]() $s_{\bot }$
can vary significantly depending on the plasma parameters. The relation between the location
$s_{\bot }$
can vary significantly depending on the plasma parameters. The relation between the location
![]() $s_{\Vert }$
and the local ‘width’ (
$s_{\Vert }$
and the local ‘width’ (
![]() ${\sim}1/W^{2}=1/(W_{\infty }^{2}{\it\kappa})$
) of the distribution given by (3.27) is accurate as long as the location of the bump is not close to unity, i.e. sufficiently far from the no-bump threshold (3.22). This justifies the approximations applied to the collision operator in our analysis. In particular, energy diffusion can be neglected since no sharp features of the distribution function in
${\sim}1/W^{2}=1/(W_{\infty }^{2}{\it\kappa})$
) of the distribution given by (3.27) is accurate as long as the location of the bump is not close to unity, i.e. sufficiently far from the no-bump threshold (3.22). This justifies the approximations applied to the collision operator in our analysis. In particular, energy diffusion can be neglected since no sharp features of the distribution function in
![]() $s_{\Vert }$
are present, as seen in figure 1(b).
$s_{\Vert }$
are present, as seen in figure 1(b).
In order to investigate the validity of our analytical calculations, we have performed a numerical analysis of the appearance of the bump by scanning the parameter space with CODE. The electron temperature and density were held constant at the values
![]() $T_{e}=1~\text{keV}$
and
$T_{e}=1~\text{keV}$
and
![]() $n_{e}=5\times 10^{18}~\text{m}^{-3}$
respectively, while the magnetic field, the induced electric field and the effective ion charge were varied over the ranges
$n_{e}=5\times 10^{18}~\text{m}^{-3}$
respectively, while the magnetic field, the induced electric field and the effective ion charge were varied over the ranges
![]() $B\in [1,6]~\text{T}$
,
$B\in [1,6]~\text{T}$
,
![]() $\hat{E}\in [2,14]$
and
$\hat{E}\in [2,14]$
and
![]() $Z_{eff}\in [1,3]$
. The numerical calculations used 950 momentum grid points, 130 Legendre modes for the decomposition in
$Z_{eff}\in [1,3]$
. The numerical calculations used 950 momentum grid points, 130 Legendre modes for the decomposition in
![]() ${\it\xi}$
, and a highest resolved momentum of
${\it\xi}$
, and a highest resolved momentum of
![]() $s=34$
, providing well-converged solutions.
$s=34$
, providing well-converged solutions.
The results of the scan are presented in figure 2, where circles and crosses correspond to distributions with and without a bump respectively. The colour coding of the circles reflects the location of the bump, with 100 % in the colour bar corresponding to
![]() $s_{\Vert }=34$
. Simulations with a bump appearing above 80 % (
$s_{\Vert }=34$
. Simulations with a bump appearing above 80 % (
![]() $s_{\Vert }=27$
) are excluded from the figure, since those results may be affected by the bump being too close to the highest resolved momentum. As expected from (3.28), increasing
$s_{\Vert }=27$
) are excluded from the figure, since those results may be affected by the bump being too close to the highest resolved momentum. As expected from (3.28), increasing
![]() $\bar{E}$
or decreasing
$\bar{E}$
or decreasing
![]() ${\it\sigma}$
moves the bump towards larger momenta.
${\it\sigma}$
moves the bump towards larger momenta.
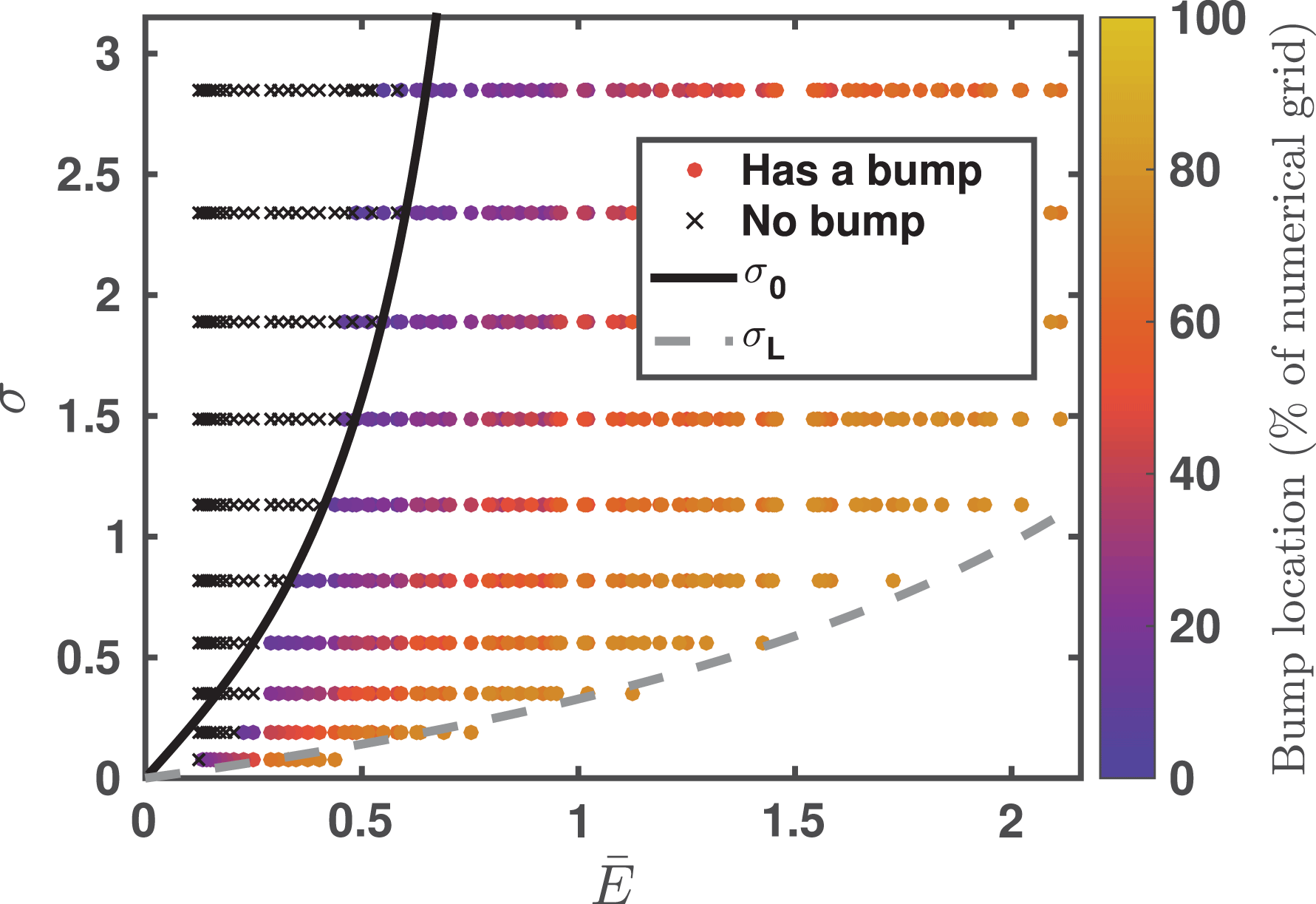
Figure 2. Parameter scan of CODE simulations yielding steady-state solutions with (coloured circles) or without (black crosses) a bump in the runaway tail. Good correlation is found with the analytical threshold condition given in (3.22) for
![]() ${\it\kappa}=1$
(solid line). The dashed line represents the ‘practical threshold’ in (3.29) for
${\it\kappa}=1$
(solid line). The dashed line represents the ‘practical threshold’ in (3.29) for
![]() $s_{\Vert ,L}=27$
and
$s_{\Vert ,L}=27$
and
![]() ${\it\kappa}=0.3$
. The colour coding shows the location of the bump relative to
${\it\kappa}=0.3$
. The colour coding shows the location of the bump relative to
![]() $s_{\Vert }=34$
.
$s_{\Vert }=34$
.
A reasonably good agreement is found between the numerical calculations and the analytical threshold for the bump to exist. The solid curve shows this threshold, (3.22), for
![]() ${\it\kappa}=1$
. Above
${\it\kappa}=1$
. Above
![]() ${\it\sigma}\approx 0.5$
the ‘no bump’ solutions obey the analytical threshold and fall to the left of the threshold curve. There are some solutions with a bump in this region as well. However, this is not surprising, since
${\it\sigma}\approx 0.5$
the ‘no bump’ solutions obey the analytical threshold and fall to the left of the threshold curve. There are some solutions with a bump in this region as well. However, this is not surprising, since
![]() ${\it\kappa}$
at the bump is allowed to be less than unity, in which case the threshold moves towards lower values of
${\it\kappa}$
at the bump is allowed to be less than unity, in which case the threshold moves towards lower values of
![]() $\bar{E}$
. The threshold begins to fail for lower values of
$\bar{E}$
. The threshold begins to fail for lower values of
![]() ${\it\sigma}$
, showing that the approximation
${\it\sigma}$
, showing that the approximation
![]() $K^{\prime }\ll \{{\it\sigma},s_{\Vert }\}$
used in (3.15) breaks down. Nevertheless, the qualitative behaviour of the threshold is still captured by (3.22). The lower right corner of the plot (high
$K^{\prime }\ll \{{\it\sigma},s_{\Vert }\}$
used in (3.15) breaks down. Nevertheless, the qualitative behaviour of the threshold is still captured by (3.22). The lower right corner of the plot (high
![]() $\bar{E}$
and small
$\bar{E}$
and small
![]() ${\it\sigma}$
) is not populated, since some simulations where the bump would have appeared at too high
${\it\sigma}$
) is not populated, since some simulations where the bump would have appeared at too high
![]() $s_{\Vert }$
were excluded. With
$s_{\Vert }$
were excluded. With
![]() $s_{\Vert ,L}=27$
, a
$s_{\Vert ,L}=27$
, a
![]() ${\it\kappa}$
value as low as 0.3 is needed in order for the limit given by (3.29) (dashed line) to correspond well to the boundary of the region of excluded points. Thus,
${\it\kappa}$
value as low as 0.3 is needed in order for the limit given by (3.29) (dashed line) to correspond well to the boundary of the region of excluded points. Thus,
![]() ${\it\kappa}$
can be significantly lower than unity at a bump with large momentum.
${\it\kappa}$
can be significantly lower than unity at a bump with large momentum.
From the parameter scan used to generate figure 2, the simulations exhibiting bumps were compared with the theoretical lower bound for the location of the bump (3.28). As shown in figure 3, we find that, indeed, the parallel momenta at the bumps (shown with green circles) are all higher than the lower bound (solid line). In fact, most of the
![]() $s_{\Vert }$
values are well above this limit. This merely confirms our finding that
$s_{\Vert }$
values are well above this limit. This merely confirms our finding that
![]() ${\it\kappa}$
at the bump is typically less than unity, especially for parameters sufficiently exceeding the no-bump threshold.
${\it\kappa}$
at the bump is typically less than unity, especially for parameters sufficiently exceeding the no-bump threshold.

Figure 3. Parallel momentum of the bump. Circles denote the locations of the bumps according to numerical solutions, while the solid line represents a theoretical lower limit, (3.28). In the simulations, all bumps appear above the analytical threshold condition.
5. Conclusions
We have analysed the runaway electron distribution function, accounting for the radiation reaction force, and have shown that the steady-state runaway distribution can become non-monotonic. Furthermore, a threshold condition for the appearance of the bump, as well as a lower limit to its location in momentum space, was derived. While slowing down and pitch angle scattering due to Coulomb collisions are taken into account in our analysis, we do not consider the effect of large-angle collisions, and we restrict the study to a straight magnetic field geometry. Our analytical results show good agreement with numerical simulations obtained using the CODE solver.
We find that for a normalized electric field larger than unity,
![]() $\bar{E}>1$
, the steady-state electron distribution always exhibits a bump, independently of the value of the
$\bar{E}>1$
, the steady-state electron distribution always exhibits a bump, independently of the value of the
![]() ${\it\sigma}$
parameter quantifying the strength of the radiation reaction, as long as the magnetic field is non-vanishing (
${\it\sigma}$
parameter quantifying the strength of the radiation reaction, as long as the magnetic field is non-vanishing (
![]() ${\it\sigma}>0$
). For a smaller electric field, the appearance of the bump is well correlated with the
${\it\sigma}>0$
). For a smaller electric field, the appearance of the bump is well correlated with the
![]() ${\it\sigma}$
threshold given by (3.22). Although above this threshold there must always be a bump in the steady-state distribution function, it may not have a practical relevance in some cases. When
${\it\sigma}$
threshold given by (3.22). Although above this threshold there must always be a bump in the steady-state distribution function, it may not have a practical relevance in some cases. When
![]() ${\it\sigma}$
is small and/or
${\it\sigma}$
is small and/or
![]() $\bar{E}$
is large, the bump would be located at a very large parallel momentum, but the forefront of the electron distribution can require a long time to reach that far. This motivates the introduction of another ‘practical’ threshold condition, (3.29). If
$\bar{E}$
is large, the bump would be located at a very large parallel momentum, but the forefront of the electron distribution can require a long time to reach that far. This motivates the introduction of another ‘practical’ threshold condition, (3.29). If
![]() ${\it\sigma}$
is lower than this threshold, the bump will appear at a momentum above some specified limit,
${\it\sigma}$
is lower than this threshold, the bump will appear at a momentum above some specified limit,
![]() $s_{\Vert ,L}$
, and can then be considered unimportant. In particular, above a normalized electric field of
$s_{\Vert ,L}$
, and can then be considered unimportant. In particular, above a normalized electric field of
![]() $\bar{E}=s_{\Vert ,L}/2$
, this criterion is satisfied for any
$\bar{E}=s_{\Vert ,L}/2$
, this criterion is satisfied for any
![]() ${\it\sigma}$
.
${\it\sigma}$
.
Nevertheless, when the radiation reaction is strong enough and/or the parallel electric field is not too high, there is a possibility for a bump to form in the runaway tail. This non-monotonic feature presents a potential source of bump-on-tail instabilities, which can play a role in limiting the formation of large runaway beams.
Acknowledgements
The authors are grateful to M. Landreman and P. Helander for fruitful discussions. This work has been carried out within the framework of the EUROfusion Consortium and has received funding from the Euratom research and training programme 2014–2018 under grant agreement no. 633053. The views and opinions expressed herein do not necessarily reflect those of the European Commission. I.P. was supported by the International Postdoc grant of Vetenskapsrådet.
Appendix A. The relativistic collision operator
The relativistic particle phase-space Beliaev–Budker collision operator in the Landau form is defined as
where
![]() ${\it\Gamma}_{ab}=e_{a}^{2}e_{b}^{2}\ln {\it\Lambda}/(4{\rm\pi}{\it\varepsilon}_{0}^{2})$
,
${\it\Gamma}_{ab}=e_{a}^{2}e_{b}^{2}\ln {\it\Lambda}/(4{\rm\pi}{\it\varepsilon}_{0}^{2})$
,
![]() $\boldsymbol{u}=\boldsymbol{p}/m_{a}$
,
$\boldsymbol{u}=\boldsymbol{p}/m_{a}$
,
![]() $\boldsymbol{u}^{\prime }=\boldsymbol{p}^{\prime }/m_{b}$
, and the collision kernel is given by
$\boldsymbol{u}^{\prime }=\boldsymbol{p}^{\prime }/m_{b}$
, and the collision kernel is given by
with the coefficients
where
![]() $\boldsymbol{K}_{ab}[\,f_{b}]$
is the friction vector and
$\boldsymbol{K}_{ab}[\,f_{b}]$
is the friction vector and
![]() $\unicode[STIX]{x1D63F}_{ab}[\,f_{b}]$
is the diffusion tensor which are defined with differential operations on Braams–Karney potentials
$\unicode[STIX]{x1D63F}_{ab}[\,f_{b}]$
is the diffusion tensor which are defined with differential operations on Braams–Karney potentials
![]() ${\it\Psi}_{n}(u)$
according to
${\it\Psi}_{n}(u)$
according to
The differential operators
![]() $\mathsf{K}$
and
$\mathsf{K}$
and
![]() $\mathsf{L}$
are defined as
$\mathsf{L}$
are defined as
In the case of isotropic background distributions
![]() $f_{b}(u)$
, the potentials become functions of
$f_{b}(u)$
, the potentials become functions of
![]() $u$
only, and the friction vector and diffusion tensor can be simplified into
$u$
only, and the friction vector and diffusion tensor can be simplified into
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D63F}_{ab} & = & \displaystyle -4{\rm\pi}{\it\Gamma}_{ab}{\it\gamma}\left({\it\Psi}_{0}-\frac{2{\it\gamma}^{2}}{u}\frac{\partial {\it\Psi}_{3}}{\partial u}+\frac{8{\it\gamma}^{2}}{uc^{2}}\frac{\partial {\it\Psi}_{4}}{\partial u}-\frac{8}{c^{4}}{\it\Psi}_{4}\right)\frac{\boldsymbol{p}\boldsymbol{p}}{p^{2}}\nonumber\\ \displaystyle & & \displaystyle \quad -\,4{\rm\pi}{\it\Gamma}_{ab}{\it\gamma}\left(\frac{1}{u}\frac{\partial {\it\Psi}_{3}}{\partial u}+\frac{1}{c^{2}}{\it\Psi}_{3}-\frac{4}{uc^{2}}\frac{\partial {\it\Psi}_{4}}{\partial u}+\frac{4}{c^{4}}{\it\Psi}_{4}\right)\left(\unicode[STIX]{x1D644}-\frac{\boldsymbol{p}\boldsymbol{p}}{p^{2}}\right)\nonumber\\ \displaystyle & \equiv & \displaystyle D_{l,ab}\frac{\boldsymbol{p}\boldsymbol{p}}{p^{2}}+D_{t,ab}\left(\unicode[STIX]{x1D644}-\frac{\boldsymbol{p}\boldsymbol{p}}{p^{2}}\right).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D63F}_{ab} & = & \displaystyle -4{\rm\pi}{\it\Gamma}_{ab}{\it\gamma}\left({\it\Psi}_{0}-\frac{2{\it\gamma}^{2}}{u}\frac{\partial {\it\Psi}_{3}}{\partial u}+\frac{8{\it\gamma}^{2}}{uc^{2}}\frac{\partial {\it\Psi}_{4}}{\partial u}-\frac{8}{c^{4}}{\it\Psi}_{4}\right)\frac{\boldsymbol{p}\boldsymbol{p}}{p^{2}}\nonumber\\ \displaystyle & & \displaystyle \quad -\,4{\rm\pi}{\it\Gamma}_{ab}{\it\gamma}\left(\frac{1}{u}\frac{\partial {\it\Psi}_{3}}{\partial u}+\frac{1}{c^{2}}{\it\Psi}_{3}-\frac{4}{uc^{2}}\frac{\partial {\it\Psi}_{4}}{\partial u}+\frac{4}{c^{4}}{\it\Psi}_{4}\right)\left(\unicode[STIX]{x1D644}-\frac{\boldsymbol{p}\boldsymbol{p}}{p^{2}}\right)\nonumber\\ \displaystyle & \equiv & \displaystyle D_{l,ab}\frac{\boldsymbol{p}\boldsymbol{p}}{p^{2}}+D_{t,ab}\left(\unicode[STIX]{x1D644}-\frac{\boldsymbol{p}\boldsymbol{p}}{p^{2}}\right).\end{eqnarray}$$
The guiding-centre transformation of the Fokker–Planck operator presented in Brizard (Reference Brizard2004) gave explicit expressions for the guiding-centre friction and diffusion coefficients,
![]() $\langle \mathscr{K}_{ab,gc}^{{\it\alpha}}\rangle$
and
$\langle \mathscr{K}_{ab,gc}^{{\it\alpha}}\rangle$
and
![]() $\langle \mathscr{D}_{ab,gc}^{{\it\alpha}{\it\beta}}\rangle$
, in the case of isotropic background distributions and a non-relativistic collision kernel. Generalization of that work to a relativistic collision kernel is straightforward in the case of isotropic field–particle distributions because the forms of the particle phase-space friction and diffusion coefficients do not change. Only the expressions for
$\langle \mathscr{D}_{ab,gc}^{{\it\alpha}{\it\beta}}\rangle$
, in the case of isotropic background distributions and a non-relativistic collision kernel. Generalization of that work to a relativistic collision kernel is straightforward in the case of isotropic field–particle distributions because the forms of the particle phase-space friction and diffusion coefficients do not change. Only the expressions for
![]() ${\it\nu}_{l,ab}$
,
${\it\nu}_{l,ab}$
,
![]() $D_{l,ab}$
, and
$D_{l,ab}$
, and
![]() $D_{t,ab}$
are different, but that will not affect the guiding-centre transformation, as they are functions only of the guiding-centre kinetic momentum.
$D_{t,ab}$
are different, but that will not affect the guiding-centre transformation, as they are functions only of the guiding-centre kinetic momentum.





