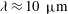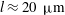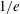1. Introduction
Laser–plasma particle accelerators can generate bunches of energetic ions with energies
![]() $\gg 1$
MeV and charge in excess of 10 nC (Daido, Nishiuchi & Pirozhkov Reference Daido, Nishiuchi and Pirozhkov2012; Macchi, Borghesi & Passoni Reference Macchi, Borghesi and Passoni2013). These promising ion sources are being developed for applications in nuclear and medical physics, many of which require control of the beam spectral shape, collimation and charge. Next-generation high-power lasers will run at 10 Hz and beyond, bringing such applications closer to realisation. However, most research on laser–plasma ion sources has used solid targets, typically metal foils of thickness
$\gg 1$
MeV and charge in excess of 10 nC (Daido, Nishiuchi & Pirozhkov Reference Daido, Nishiuchi and Pirozhkov2012; Macchi, Borghesi & Passoni Reference Macchi, Borghesi and Passoni2013). These promising ion sources are being developed for applications in nuclear and medical physics, many of which require control of the beam spectral shape, collimation and charge. Next-generation high-power lasers will run at 10 Hz and beyond, bringing such applications closer to realisation. However, most research on laser–plasma ion sources has used solid targets, typically metal foils of thickness
![]() ${\sim}1~{\rm\mu}\text{m}$
. At high repetition rate, using such targets raises significant challenges with debris, target insertion and unwanted secondary radiation such as bremsstrahlung.
${\sim}1~{\rm\mu}\text{m}$
. At high repetition rate, using such targets raises significant challenges with debris, target insertion and unwanted secondary radiation such as bremsstrahlung.
Easily replenished, debris-free gaseous targets would alleviate many of these problems. They can generate single-species ion beams, which are challenging for solid targets due to the hydrocarbon layers that typically form on their surface. Previous work has demonstrated longitudinal (along the laser-axis) (Willingale et al.
Reference Willingale, Mangles, Nilson, Clarke, Dangor, Kaluza, Karsch, Lancaster, Mori and Najmudin2006) and transverse (perpendicular to the laser-axis) (Krushelnick et al.
Reference Krushelnick, Clark, Najmudin, Salvati, Santala, Tatarakis, Dangor, Malka, Neely and Allott1999; Wei et al.
Reference Wei, Mangles, Najmudin, Walton, Gopal, Tatarakis, Dangor, Clark, Evans and Fritzler2004; Sylla et al.
Reference Sylla, Veltcheva, Kahaly, Flacco and Malka2012; Lifschitz et al.
Reference Lifschitz, Sylla, Kahaly, Flacco, Veltcheva, Sanchez-Arriaga, Lefebvre and Malka2014) acceleration of helium ions from targets below the relativistic critical density at which the plasma becomes opaque to the laser
![]() $n_{cr}=\bar{{\it\gamma}}n_{c}=\bar{{\it\gamma}}{\it\epsilon}_{0}m_{e}{\it\omega}_{L}^{2}/e^{2}$
, where
$n_{cr}=\bar{{\it\gamma}}n_{c}=\bar{{\it\gamma}}{\it\epsilon}_{0}m_{e}{\it\omega}_{L}^{2}/e^{2}$
, where
![]() $\bar{{\it\gamma}}$
is the cycle-averaged electron Lorentz factor,
$\bar{{\it\gamma}}$
is the cycle-averaged electron Lorentz factor,
![]() $n_{c}$
is the critical density and
$n_{c}$
is the critical density and
![]() ${\it\omega}_{L}$
is the laser frequency. However, transverse acceleration creates a divergent expansion of the ions, making it not suitable for high flux applications, whilst longitudinal acceleration from underdense targets has only been reported using laser intensities in excess of
${\it\omega}_{L}$
is the laser frequency. However, transverse acceleration creates a divergent expansion of the ions, making it not suitable for high flux applications, whilst longitudinal acceleration from underdense targets has only been reported using laser intensities in excess of
![]() $10^{20}~\text{W}~\text{cm}^{-2}$
and longer
$10^{20}~\text{W}~\text{cm}^{-2}$
and longer
![]() ${\sim}1$
ps pulses as the produced longitudinal accelerating fields are low compared to thin foil targets (Willingale et al.
Reference Willingale, Mangles, Nilson, Clarke, Dangor, Kaluza, Karsch, Lancaster, Mori and Najmudin2006).
${\sim}1$
ps pulses as the produced longitudinal accelerating fields are low compared to thin foil targets (Willingale et al.
Reference Willingale, Mangles, Nilson, Clarke, Dangor, Kaluza, Karsch, Lancaster, Mori and Najmudin2006).
More recently, the development of high-power CO
![]() $_{2}$
lasers (Haberberger, Tochitsky & Joshi Reference Haberberger, Tochitsky and Joshi2010; Polyanskiy, Pogorelsky & Yakimenko Reference Polyanskiy, Pogorelsky and Yakimenko2011), for which the wavelength
$_{2}$
lasers (Haberberger, Tochitsky & Joshi Reference Haberberger, Tochitsky and Joshi2010; Polyanskiy, Pogorelsky & Yakimenko Reference Polyanskiy, Pogorelsky and Yakimenko2011), for which the wavelength
![]() ${\it\lambda}_{L}\approx 10~{\rm\mu}\text{m}$
results in a critical density
${\it\lambda}_{L}\approx 10~{\rm\mu}\text{m}$
results in a critical density
![]() $n_{c}\approx 10^{19}~\text{cm}^{-3}$
, has allowed studies with gaseous targets at densities greater than
$n_{c}\approx 10^{19}~\text{cm}^{-3}$
, has allowed studies with gaseous targets at densities greater than
![]() $n_{cr}$
. Using an opaque but near-critical density target combined with a laser pulse of a few ps results in the generation of an electrostatic collisionless shock (Denavit Reference Denavit1992; Silva et al.
Reference Silva, Marti, Davies, Fonseca, Ren and Mori2004; Fiuza et al.
Reference Fiuza, Stockem, Boella, Fonseca, Silva, Haberberger, Tochitsky, Gong, Mori and Joshi2012) capable of accelerating a fraction of the background ions to a velocity twice the speed of the shock,
$n_{cr}$
. Using an opaque but near-critical density target combined with a laser pulse of a few ps results in the generation of an electrostatic collisionless shock (Denavit Reference Denavit1992; Silva et al.
Reference Silva, Marti, Davies, Fonseca, Ren and Mori2004; Fiuza et al.
Reference Fiuza, Stockem, Boella, Fonseca, Silva, Haberberger, Tochitsky, Gong, Mori and Joshi2012) capable of accelerating a fraction of the background ions to a velocity twice the speed of the shock,
![]() $v_{i}=2v_{s}$
. Initial experiments accelerated protons to energies in excess of 1 MeV with a small energy spread via this technique (Palmer et al.
Reference Palmer, Dover, Pogorelsky, Babzien, Dudnikova, Ispiriyan, Polyanskiy, Schreiber, Shkolnikov and Yakimenko2011) and subsequently higher ion energies were produced when a longer, more energetic laser pulse drove the acceleration (Haberberger et al.
Reference Haberberger, Tochitsky, Fiuza, Gong, Fonseca, Silva, Mori and Joshi2012).
$v_{i}=2v_{s}$
. Initial experiments accelerated protons to energies in excess of 1 MeV with a small energy spread via this technique (Palmer et al.
Reference Palmer, Dover, Pogorelsky, Babzien, Dudnikova, Ispiriyan, Polyanskiy, Schreiber, Shkolnikov and Yakimenko2011) and subsequently higher ion energies were produced when a longer, more energetic laser pulse drove the acceleration (Haberberger et al.
Reference Haberberger, Tochitsky, Fiuza, Gong, Fonseca, Silva, Mori and Joshi2012).
Both of these experiments were driven by a train of intense pulses, characteristic of short-pulse CO
![]() $_{2}$
systems. The pulse train played an essential role in creating a suitable plasma density distribution, resulting in enhanced radiation pressure and stronger laser absorption, leading to the generation of an accelerating electrostatic collisionless shock. However, the shot-to-shot variation in the CO
$_{2}$
systems. The pulse train played an essential role in creating a suitable plasma density distribution, resulting in enhanced radiation pressure and stronger laser absorption, leading to the generation of an accelerating electrostatic collisionless shock. However, the shot-to-shot variation in the CO
![]() $_{2}$
pulse train meant the density distribution also varied from shot-to-shot, affecting the reproducibility of the ion beam. Recent breakthroughs with CO
$_{2}$
pulse train meant the density distribution also varied from shot-to-shot, affecting the reproducibility of the ion beam. Recent breakthroughs with CO
![]() $_{2}$
laser technology have allowed the isolation of a single intense pulse, permitting more control over the laser–plasma interaction (Polyanskiy et al.
Reference Polyanskiy, Pogorelsky and Yakimenko2011). However, typical gas-jet targets have linear or parabolic density scale-lengths
$_{2}$
laser technology have allowed the isolation of a single intense pulse, permitting more control over the laser–plasma interaction (Polyanskiy et al.
Reference Polyanskiy, Pogorelsky and Yakimenko2011). However, typical gas-jet targets have linear or parabolic density scale-lengths
![]() $\gg 100~{\rm\mu}\text{m}$
, too long for the production of quasi-monoenergetic ion beams (Palmer et al.
Reference Palmer, Dover, Pogorelsky, Streeter and Najmudin2014).
$\gg 100~{\rm\mu}\text{m}$
, too long for the production of quasi-monoenergetic ion beams (Palmer et al.
Reference Palmer, Dover, Pogorelsky, Streeter and Najmudin2014).
It has been shown that secondary laser pulses can be used to ‘machine’ gas targets. Periodic structures have been created by irradiating gas with a spatially modulated intense laser and waiting for hydrodynamic expansion to create density perturbations in the gas (Pai et al. Reference Pai, Huang, Kuo, Lin, Wang, Chen, Lee and Lin2005). A similar set-up was used to dynamically control the length of gas jets for investigating laser wakefield electron acceleration (Hsieh et al. Reference Hsieh, Huang, Chang, Ho, Chen, Lin, Wang and Chen2006). More recently, Kaganovich et al. (Reference Kaganovich, Gordon, Helle and Ting2014) focused a secondary pulse on a foil near the gas flow to drive a hydrodynamic shock into the gas to create density discontinuities.
In this paper, we outline a method for optically shaping a gas target for application to ion acceleration. An all-optical target manipulation system was developed to modify the density profiles of gas targets by using a
![]() ${\sim}10{-}100~\text{mJ}$
prepulse arriving 25 ns before the main intense pulse. This prepulse is absorbed locally and heats a small region of gas, which subsequently expands and forms a blast wave. By varying the prepulse we were able to decrease the front density scale-lengths down to
${\sim}10{-}100~\text{mJ}$
prepulse arriving 25 ns before the main intense pulse. This prepulse is absorbed locally and heats a small region of gas, which subsequently expands and forms a blast wave. By varying the prepulse we were able to decrease the front density scale-lengths down to
![]() ${\approx}30~{\rm\mu}\text{m}$
(
${\approx}30~{\rm\mu}\text{m}$
(
![]() $1/e$
). These targets were subsequently used (Tresca et al.
Reference Tresca, Dover, Cook, Maharjan, Polyanskiy, Najmudin, Shkolnikov and Pogorelsky2015) to generate reproducible proton and helium beams with energies up to
$1/e$
). These targets were subsequently used (Tresca et al.
Reference Tresca, Dover, Cook, Maharjan, Polyanskiy, Najmudin, Shkolnikov and Pogorelsky2015) to generate reproducible proton and helium beams with energies up to
![]() $E\sim 1~\text{MeV}$
.
$E\sim 1~\text{MeV}$
.
This paper gives a detailed overview of the generation of a prepulse induced blast wave. In § 2 we discuss analytical scalings of the blast-wave parameters and the resultant density profile, and support this with numerical hydrodynamic simulation to explain and predict the blast-wave properties. This is followed by § 3 demonstrating experimentally the effect of changing the prepulse energy on the plasma density profile. We finally discuss briefly the effects of the density gradients on the laser–plasma interaction and propose an extension to blast-wave shaping of higher-density targets of interest to ion acceleration using higher-intensity near-IR lasers.
2. Modelling of prepulse-driven blast waves
A tightly focussed laser pulse of sufficient intensity can induce breakdown of the target gas, forming a plasma which then absorbs energy from the pulse. For sufficiently low plasma temperatures and laser intensities inverse bremsstrahlung heating dominates, in which electrons gain energy from the incident laser field before locally depositing the energy in the plasma via collisions with nearby ions.
The electron–ion collision frequency is given by
where
![]() $n_{e}$
is the plasma electron density,
$n_{e}$
is the plasma electron density,
![]() $\ln {\it\Lambda}$
is the Coulomb logarithm,
$\ln {\it\Lambda}$
is the Coulomb logarithm,
![]() $Z$
is the atomic number,
$Z$
is the atomic number,
![]() $k_{b}$
is the Boltzmann constant and
$k_{b}$
is the Boltzmann constant and
![]() $T_{e}$
is the electron temperature. Note that the free electron density depends on the ionisation fraction, which can evolve dynamically as an increasing amount of energy is absorbed in the plasma. The absorption coefficient for inverse bremsstrahlung is given by
$T_{e}$
is the electron temperature. Note that the free electron density depends on the ionisation fraction, which can evolve dynamically as an increasing amount of energy is absorbed in the plasma. The absorption coefficient for inverse bremsstrahlung is given by
and the corresponding fraction of laser energy thermally absorbed by the plasma,
![]() ${\it\eta}=E_{abs}/E_{L}$
, is then given by
${\it\eta}=E_{abs}/E_{L}$
, is then given by
where the integral is taken along the laser path (Kruer Reference Kruer1988). As laser energy is absorbed, the plasma heats up, reducing the collision frequency and hence the laser absorption. Therefore
![]() ${\it\eta}$
depends on the target and focusing parameters.
${\it\eta}$
depends on the target and focusing parameters.
A simplified quantitative model can be introduced for a hydrogen (
![]() $Z=1$
) target by neglecting energy loss to ionisation and assuming full ionisation. For an isotropic initial gas density profile, and assuming the breakdown and laser absorption only occur when the laser intensity is at its maximum at the laser focus (
$Z=1$
) target by neglecting energy loss to ionisation and assuming full ionisation. For an isotropic initial gas density profile, and assuming the breakdown and laser absorption only occur when the laser intensity is at its maximum at the laser focus (
![]() $-Z_{R}/2<x<Z_{R}/2$
, where
$-Z_{R}/2<x<Z_{R}/2$
, where
![]() $Z_{R}$
is the Rayleigh range), this can be simplified to
$Z_{R}$
is the Rayleigh range), this can be simplified to
![]() ${\it\eta}\simeq 1-\exp (-KZ_{R})$
. In practice the discharge region may differ from this, particularly for larger prepulse energies with intensities exceeding the breakdown threshold away from focus. Assuming uniform heating over a volume bounded by the laser focal spot and
${\it\eta}\simeq 1-\exp (-KZ_{R})$
. In practice the discharge region may differ from this, particularly for larger prepulse energies with intensities exceeding the breakdown threshold away from focus. Assuming uniform heating over a volume bounded by the laser focal spot and
![]() $Z_{R}$
and no hydrodynamic expansion, and using (2.3) for the amount of energy absorbed as the laser transmits through the plasma, the plasma temperature is given by
$Z_{R}$
and no hydrodynamic expansion, and using (2.3) for the amount of energy absorbed as the laser transmits through the plasma, the plasma temperature is given by
where
![]() $I_{L}$
is the laser intensity.
$I_{L}$
is the laser intensity.
In the strongly absorbing limit (
![]() $KZ_{R}\gg 1$
), this gives
$KZ_{R}\gg 1$
), this gives
![]() $T_{e}\propto t$
. However, for most of the parameter space considered here,
$T_{e}\propto t$
. However, for most of the parameter space considered here,
![]() $KZ_{R}<1$
. In the very low absorption limit (
$KZ_{R}<1$
. In the very low absorption limit (
![]() $KZ_{R}\ll 1$
) and assuming constant
$KZ_{R}\ll 1$
) and assuming constant
![]() $\ln \,{\it\Lambda}$
,
$\ln \,{\it\Lambda}$
,
where
![]() $T_{0}$
is the initial temperature and
$T_{0}$
is the initial temperature and
The approximation required for this analytical solution is not valid for either
![]() $n_{e}\approx n_{c}$
, nor for
$n_{e}\approx n_{c}$
, nor for
![]() $T_{e}\gg T_{0}$
, since then
$T_{e}\gg T_{0}$
, since then
![]() $\ln \,{\it\Lambda}$
changes significantly over the prepulse-target interaction. Therefore, to test the largest possible range of parameters we instead integrate (2.4) numerically to model the heating.
$\ln \,{\it\Lambda}$
changes significantly over the prepulse-target interaction. Therefore, to test the largest possible range of parameters we instead integrate (2.4) numerically to model the heating.
Figure 1(a) shows
![]() $T_{e}$
as a function of time with
$T_{e}$
as a function of time with
![]() ${\it\lambda}_{L}=10~{\rm\mu}\text{m}$
, pulse duration
${\it\lambda}_{L}=10~{\rm\mu}\text{m}$
, pulse duration
![]() ${\it\tau}_{L}=5~\text{ps}$
with a top-hat temporal intensity profile, focal spot size
${\it\tau}_{L}=5~\text{ps}$
with a top-hat temporal intensity profile, focal spot size
![]() $70~{\rm\mu}\text{m}$
spot and Rayleigh length
$70~{\rm\mu}\text{m}$
spot and Rayleigh length
![]() $Z_{R}=300~{\rm\mu}\text{m}$
propagating into a fixed plasma density
$Z_{R}=300~{\rm\mu}\text{m}$
propagating into a fixed plasma density
![]() $n_{e}=n_{i}=5\times 10^{18}~\text{cm}^{-3}$
(
$n_{e}=n_{i}=5\times 10^{18}~\text{cm}^{-3}$
(
![]() $0.5n_{c}$
for
$0.5n_{c}$
for
![]() ${\it\lambda}=10~{\rm\mu}\text{m}$
) solved with an initial temperature
${\it\lambda}=10~{\rm\mu}\text{m}$
) solved with an initial temperature
![]() $T_{0}=10$
eV for different laser energies. Due to the low initial temperature, the initial absorption fraction is high. The laser energy is efficiently converted into thermal energy and the temperature increases rapidly. However, as the plasma temperature rises, the collision frequency reduces and the rate of laser absorption decreases.
$T_{0}=10$
eV for different laser energies. Due to the low initial temperature, the initial absorption fraction is high. The laser energy is efficiently converted into thermal energy and the temperature increases rapidly. However, as the plasma temperature rises, the collision frequency reduces and the rate of laser absorption decreases.

Figure 1. (a) Temperature as a function of time for varying laser energy and fixed laser focus (
![]() ${\it\lambda}_{L}=10~{\rm\mu}\text{m}$
, focal spot size
${\it\lambda}_{L}=10~{\rm\mu}\text{m}$
, focal spot size
![]() $70~{\rm\mu}\text{m}$
,
$70~{\rm\mu}\text{m}$
,
![]() $Z_{R}=300~{\rm\mu}\text{m}$
,
$Z_{R}=300~{\rm\mu}\text{m}$
,
![]() ${\it\tau}_{L}=5$
ps) and density (hydrogen,
${\it\tau}_{L}=5$
ps) and density (hydrogen,
![]() $n_{e}=n_{i}=0.5n_{c}$
). (b) Absorption fraction of incident laser light
$n_{e}=n_{i}=0.5n_{c}$
). (b) Absorption fraction of incident laser light
![]() ${\it\eta}$
(solid lines) and total energy absorbed
${\it\eta}$
(solid lines) and total energy absorbed
![]() $E_{abs}$
(dotted lines) as a function of target density for various laser energies.
$E_{abs}$
(dotted lines) as a function of target density for various laser energies.
Figure 1(b) shows the absorbed fraction
![]() ${\it\eta}$
and deposited energy
${\it\eta}$
and deposited energy
![]() $E_{abs}$
for different laser energies after irradiation as a function of target density. For a given density, higher energy pulses deposit a smaller fraction of their energy. However, as the absorption coefficient
$E_{abs}$
for different laser energies after irradiation as a function of target density. For a given density, higher energy pulses deposit a smaller fraction of their energy. However, as the absorption coefficient
![]() $K$
(2.2) tends to infinity for
$K$
(2.2) tends to infinity for
![]() $n_{e}=n_{c}$
, high absorption is recovered by increasing target density, as has been shown experimentally for longer pulses (Mori, Komurasaki & Arakawa Reference Mori, Komurasaki and Arakawa2004). For sufficiently high initial gas density, if the plasma reaches an ionisation state such that
$n_{e}=n_{c}$
, high absorption is recovered by increasing target density, as has been shown experimentally for longer pulses (Mori, Komurasaki & Arakawa Reference Mori, Komurasaki and Arakawa2004). For sufficiently high initial gas density, if the plasma reaches an ionisation state such that
![]() $n_{e}>n_{c}$
, the prepulse will cease to transmit through the target and instead be reflected at the critical surface, causing the above model to break down. Note that this model neglects breakdown and ionisation; decreasing the prepulse energy below the breakdown threshold will result in no absorption. Furthermore, it considers only collisional heating whereas further absorption may occur from coupling to parametric instabilities or resonances.
$n_{e}>n_{c}$
, the prepulse will cease to transmit through the target and instead be reflected at the critical surface, causing the above model to break down. Note that this model neglects breakdown and ionisation; decreasing the prepulse energy below the breakdown threshold will result in no absorption. Furthermore, it considers only collisional heating whereas further absorption may occur from coupling to parametric instabilities or resonances.
Over a 5 ps pulse duration, the hydrodynamic expansion of the plasma is negligible. However, after the initial energy deposition, the heated plasma will expand into the surrounding ambient medium as a collisional blast wave (Sedov Reference Sedov1959; Zel’dovich & Raizer Reference Zel’dovich and Raizer1966). A cavity forms surrounded by a dense wall at the expanding shock front. Whilst the blast-wave shock is strongly driven (i.e. the pressure ahead of the shock is negligible compared to the pressure behind the shock), the equations of motion follow a self-similar solution (Sedov Reference Sedov1959). The radius of the blast wave at time
![]() $t$
is then given by
$t$
is then given by
where
![]() ${\it\alpha}=2(3)$
is the dimensionality of the shock for a cylindrically (spherically) expanding shock,
${\it\alpha}=2(3)$
is the dimensionality of the shock for a cylindrically (spherically) expanding shock,
![]() ${\it\rho}$
is the mass density of the background fluid, and
${\it\rho}$
is the mass density of the background fluid, and
![]() ${\it\zeta}_{0}({\it\gamma})$
is a numerical constant
${\it\zeta}_{0}({\it\gamma})$
is a numerical constant
![]() ${\sim}1$
which is a function of the ratio of specific heats
${\sim}1$
which is a function of the ratio of specific heats
![]() ${\it\gamma}$
and the dimensionality
${\it\gamma}$
and the dimensionality
![]() ${\it\alpha}$
(Sedov Reference Sedov1959). Therefore, the blast-wave size is dependent on the energy absorbed from the laser prepulse, which, as was shown in figure 1, itself varies on target and laser parameters. Although the prepulse may initially heat a cylinder of gas, as
${\it\alpha}$
(Sedov Reference Sedov1959). Therefore, the blast-wave size is dependent on the energy absorbed from the laser prepulse, which, as was shown in figure 1, itself varies on target and laser parameters. Although the prepulse may initially heat a cylinder of gas, as
![]() $r_{bw}\gg Z_{r}$
, the expansion becomes increasingly three dimensional and the expansion is best described as a spherically expanding shock (
$r_{bw}\gg Z_{r}$
, the expansion becomes increasingly three dimensional and the expansion is best described as a spherically expanding shock (
![]() ${\it\alpha}=3$
). Although the above solution is valid for a homogenous target distribution, real gas-jet targets will have density gradients affecting shock propagation. Shockwave expansion in density gradients is also of importance to, for example, supernova explosions in astrophysics (see e.g. review by Ostriker & McKee (Reference Ostriker and McKee1988)). For example, the well-known Kompaneets equation describes a blast wave expanding into an exponentially varying density profile of the form
${\it\alpha}=3$
). Although the above solution is valid for a homogenous target distribution, real gas-jet targets will have density gradients affecting shock propagation. Shockwave expansion in density gradients is also of importance to, for example, supernova explosions in astrophysics (see e.g. review by Ostriker & McKee (Reference Ostriker and McKee1988)). For example, the well-known Kompaneets equation describes a blast wave expanding into an exponentially varying density profile of the form
![]() ${\it\rho}(x)\propto \exp (-x/l)$
, where
${\it\rho}(x)\propto \exp (-x/l)$
, where
![]() $l$
is the exponential scale-length (Kompaneets Reference Kompaneets1960).
$l$
is the exponential scale-length (Kompaneets Reference Kompaneets1960).
To test arbitrary density profiles and initial deposition-region characteristics, we performed hydrodynamic simulations of the blast-wave expansion using the FLASH hydrodynamics solver in 2-D cylindrical symmetry. Initially, the target was set to be homogenous with density
![]() ${\it\rho}=8\times 10^{-5}$
g cm
${\it\rho}=8\times 10^{-5}$
g cm
![]() $^{-3}$
corresponding to a number density
$^{-3}$
corresponding to a number density
![]() $n_{e}=n_{i}\approx 5\times 10^{19}$
cm
$n_{e}=n_{i}\approx 5\times 10^{19}$
cm
![]() $^{-3}$
, temperature
$^{-3}$
, temperature
![]() $T_{i}=293$
K and a fixed specific heat ratio
$T_{i}=293$
K and a fixed specific heat ratio
![]() ${\it\gamma}=1.4$
, describing a hydrogen-gas target for laser–plasma interactions. Note that the temperature of gas puffed from a gas jet is likely to be lower than this as it expands into the vacuum, and will depend on the nozzle geometry. However, the counter pressure of the ambient medium is negligible in the conditions simulated, and so does not affect the applicability to experiment. A spherical region with radius
${\it\gamma}=1.4$
, describing a hydrogen-gas target for laser–plasma interactions. Note that the temperature of gas puffed from a gas jet is likely to be lower than this as it expands into the vacuum, and will depend on the nozzle geometry. However, the counter pressure of the ambient medium is negligible in the conditions simulated, and so does not affect the applicability to experiment. A spherical region with radius
![]() $r_{dep}\approx w_{L}=70~{\rm\mu}\text{m}$
of fluid was initialised with thermal energy
$r_{dep}\approx w_{L}=70~{\rm\mu}\text{m}$
of fluid was initialised with thermal energy
![]() $E_{abs}$
, and simulated for 25 ns.
$E_{abs}$
, and simulated for 25 ns.

Figure 2. (a) Radial density profile of a spherical blast wave from FLASH simulation with
![]() $\text{AMR}=6$
(blue) and 8 (red). The black line is the analytical self-similar solution. (b) Simulated blast-wave position as a function of time for different
$\text{AMR}=6$
(blue) and 8 (red). The black line is the analytical self-similar solution. (b) Simulated blast-wave position as a function of time for different
![]() $E_{abs}$
and fixed density
$E_{abs}$
and fixed density
![]() ${\it\rho}=8\times 10^{-5}$
g cm
${\it\rho}=8\times 10^{-5}$
g cm
![]() $^{-3}$
, equivalent to
$^{-3}$
, equivalent to
![]() $n_{i}=n_{e}\approx 5\times 10^{19}$
cm
$n_{i}=n_{e}\approx 5\times 10^{19}$
cm
![]() $^{-3}$
for hydrogen. Dotted lines are analytical fits from (2.7).
$^{-3}$
for hydrogen. Dotted lines are analytical fits from (2.7).
The heated region quickly expands, within 1 ns forming an evacuated cavity with increasing density around the edge up to a shock front. The blast-wave shock expands into the ambient gas. FLASH features adaptive mesh refinement, AMR, allowing higher resolution around shock-fronts which provides a more accurate simulation of the blast-wave wall. The effect of increasing AMR can be seen in figure 2(a), on a normalised axis together with the self-similar solution (Sedov Reference Sedov1959). Increasing AMR brings the solution closer to the analytical solution, although the finite grid means the peak density is still slightly lower in the simulation. Indeed, the peak density in the blast wave should reach the strong shock limit,
Gases with lower
![]() ${\it\gamma}$
therefore give higher maximum densities in the blast wave. The width of the shock front, the distance between the peak of the density front and the ambient medium, is determined by the mean free path, and is smaller than the simulation resolution. Figure 2(b) shows the blast-wave expansion as a function of time for varying
${\it\gamma}$
therefore give higher maximum densities in the blast wave. The width of the shock front, the distance between the peak of the density front and the ambient medium, is determined by the mean free path, and is smaller than the simulation resolution. Figure 2(b) shows the blast-wave expansion as a function of time for varying
![]() $E_{abs}$
. The analytical fits, calculated from (2.7) for spherical expansion and
$E_{abs}$
. The analytical fits, calculated from (2.7) for spherical expansion and
![]() ${\it\gamma}=1.4$
,
${\it\gamma}=1.4$
,
![]() ${\it\zeta}_{0}\approx 1.175^{0.2}$
(Sedov Reference Sedov1959), are also plotted, showing good agreement with the fluid simulation.
${\it\zeta}_{0}\approx 1.175^{0.2}$
(Sedov Reference Sedov1959), are also plotted, showing good agreement with the fluid simulation.
For applications to laser-driven shockwave acceleration of ions, a key quantity is the scale-length between the vacuum region and critical density surface. Steeper density gradients allow stronger localised energy deposition and can enhance shockwave generation (Palmer et al.
Reference Palmer, Dover, Pogorelsky, Streeter and Najmudin2014; Tresca et al.
Reference Tresca, Dover, Cook, Maharjan, Polyanskiy, Najmudin, Shkolnikov and Pogorelsky2015). To achieve a steep vacuum–plasma interface, a blast wave can be generated in the gas target close enough to the gas-jet edge that the shock expands into the vacuum region. The gas nozzle used in previous ion-generation experiments with high-intensity CO
![]() $_{2}$
lasers has a gas profile at laser focus height
$_{2}$
lasers has a gas profile at laser focus height
![]() ${\approx}1$
mm above the gas-jet exit that is well approximated by a triangle with side lengths
${\approx}1$
mm above the gas-jet exit that is well approximated by a triangle with side lengths
![]() ${\approx}800~{\rm\mu}\text{m}$
(Najmudin et al.
Reference Najmudin, Palmer, Dover, Pogorelsky, Babzien, Dangor, Dudnikova, Foster, Green and Ispiriyan2011).
${\approx}800~{\rm\mu}\text{m}$
(Najmudin et al.
Reference Najmudin, Palmer, Dover, Pogorelsky, Babzien, Dangor, Dudnikova, Foster, Green and Ispiriyan2011).
To model the blast-wave expansion for this nozzle, further simulations were performed using this initial gas density profile. The gentle density gradient of the gas jet parallel to the nozzle flow was neglected to allow the use of 2-D cylindrical geometry. The hydrogen gas was initialised as a triangle with a peak density equivalent to
![]() $n_{p}=n_{e}=5\times 10^{19}$
cm
$n_{p}=n_{e}=5\times 10^{19}$
cm
![]() $^{-3}$
, and side length
$^{-3}$
, and side length
![]() $800~{\rm\mu}\text{m}$
. Outside the gas-jet region, the density was set to be 1000 times lower than
$800~{\rm\mu}\text{m}$
. Outside the gas-jet region, the density was set to be 1000 times lower than
![]() $n_{p}$
. Note that this provides a counter pressure that is negligible, and approximates the low pressure ‘vacuum’ outside of the gas jet.
$n_{p}$
. Note that this provides a counter pressure that is negligible, and approximates the low pressure ‘vacuum’ outside of the gas jet.
Thermal energy was initially deposited as a sphere with radius
![]() $70~{\rm\mu}\text{m}$
at a position
$70~{\rm\mu}\text{m}$
at a position
![]() $200~{\rm\mu}\text{m}$
from the peak density. The subsequent expansion for three different initial energies is given in figure 3(a–c) at 25 ns after the start of the simulation. For
$200~{\rm\mu}\text{m}$
from the peak density. The subsequent expansion for three different initial energies is given in figure 3(a–c) at 25 ns after the start of the simulation. For
![]() $E_{abs}=1$
mJ, expansion is approximately spherical and the cavity has not expanded into the vacuum region. At
$E_{abs}=1$
mJ, expansion is approximately spherical and the cavity has not expanded into the vacuum region. At
![]() $E_{abs}=10$
mJ, the shock slows more quickly in the high-density region than for low density. Hence the blast wave has opened up into the ‘vacuum’ region, leaving a highly asymmetric cavity. For even higher
$E_{abs}=10$
mJ, the shock slows more quickly in the high-density region than for low density. Hence the blast wave has opened up into the ‘vacuum’ region, leaving a highly asymmetric cavity. For even higher
![]() $E_{abs}$
, the blast wave exits from the rear side of the gas jet (figure 3
c).
$E_{abs}$
, the blast wave exits from the rear side of the gas jet (figure 3
c).

Figure 3. (a–c) Gas particle density distribution at
![]() $t=25$
ns after energy deposition for
$t=25$
ns after energy deposition for
![]() $E_{abs}=1$
, 10, 100 mJ respectively with initial triangular-shaped density profile. (d) The laser-axis (
$E_{abs}=1$
, 10, 100 mJ respectively with initial triangular-shaped density profile. (d) The laser-axis (
![]() $y=0$
) density distribution at different times in the expansion for
$y=0$
) density distribution at different times in the expansion for
![]() $E_{abs}=100$
mJ.
$E_{abs}=100$
mJ.
The density profile on the laser-axis at different times is given in figure 3(d) for a deposited energy of
![]() $E_{abs}=100$
mJ. The blast wave produces densities in excess of the initial maximum density, and steep density features in the gas. The steepness of the density ramp
$E_{abs}=100$
mJ. The blast wave produces densities in excess of the initial maximum density, and steep density features in the gas. The steepness of the density ramp
![]() $l$
can be estimated by fitting an exponential density profile
$l$
can be estimated by fitting an exponential density profile
![]() ${\it\rho}={\it\rho}_{max}\text{e}^{(x-x_{0})/l}$
in the region of the shock ramp, and is 22, 45,
${\it\rho}={\it\rho}_{max}\text{e}^{(x-x_{0})/l}$
in the region of the shock ramp, and is 22, 45,
![]() $180~{\rm\mu}\text{m}$
for 1, 5 and 25 ns respectively. Evidently the scale-length increases with increasing time. The asymmetry caused by deposition of energy off the centre of the gas jet results in a time window between the blast wave opening up to vacuum on the down ramp side, and before the density gradient has lengthened too much. Within this time window a high-intensity pulse can interact with a steep density profile and a higher peak density than otherwise available in the gas jet.
$180~{\rm\mu}\text{m}$
for 1, 5 and 25 ns respectively. Evidently the scale-length increases with increasing time. The asymmetry caused by deposition of energy off the centre of the gas jet results in a time window between the blast wave opening up to vacuum on the down ramp side, and before the density gradient has lengthened too much. Within this time window a high-intensity pulse can interact with a steep density profile and a higher peak density than otherwise available in the gas jet.
3. Experimental realisation of gas-jet shaping
To demonstrate blast-wave shaping of gas jets and its effect on ion shockwave acceleration, we performed an experiment using the high-intensity CO
![]() $_{2}$
laser (
$_{2}$
laser (
![]() ${\it\lambda}_{L}=10.3~{\rm\mu}\text{m}$
) at the Accelerator Test Facility, Brookhaven National Laboratory. A linearly polarised single
${\it\lambda}_{L}=10.3~{\rm\mu}\text{m}$
) at the Accelerator Test Facility, Brookhaven National Laboratory. A linearly polarised single
![]() ${\approx}10$
J pulse of duration
${\approx}10$
J pulse of duration
![]() ${\it\tau}_{L}\approx 5$
ps was focused to a spot
${\it\tau}_{L}\approx 5$
ps was focused to a spot
![]() $w_{0}=65~{\rm\mu}\text{m}$
. This provided a maximal peak intensity
$w_{0}=65~{\rm\mu}\text{m}$
. This provided a maximal peak intensity
![]() $I_{L}=2.5\times 10^{16}$
W cm
$I_{L}=2.5\times 10^{16}$
W cm
![]() $^{-2}$
, corresponding to a normalised vector potential
$^{-2}$
, corresponding to a normalised vector potential
![]() $a_{0}=1.4$
. A prepulse with variable energy (
$a_{0}=1.4$
. A prepulse with variable energy (
![]() ${\it\tau}_{pp}=5$
ps) arrived 25 ns before the main intense pulse. The energy of the prepulse was measured on shot with a photodiode which had been cross-calibrated using a calorimeter. The Rayleigh length of the focal spot was measured to be
${\it\tau}_{pp}=5$
ps) arrived 25 ns before the main intense pulse. The energy of the prepulse was measured on shot with a photodiode which had been cross-calibrated using a calorimeter. The Rayleigh length of the focal spot was measured to be
![]() $Z_{R}\approx 400~{\rm\mu}\text{m}$
.
$Z_{R}\approx 400~{\rm\mu}\text{m}$
.

Figure 4. (a–c) Raw interferometry, extracted phase (units are radians) and Abel inverted electron-density profile (units are
![]() $10^{19}$
cm
$10^{19}$
cm
![]() $^{-3}$
) imaged 250 ps after irradiation of a He target with a 280 mJ pulse. (d) Line-out along laser-axis of electron density (red) and the neutral-gas density (blue, if doubly ionised).
$^{-3}$
) imaged 250 ps after irradiation of a He target with a 280 mJ pulse. (d) Line-out along laser-axis of electron density (red) and the neutral-gas density (blue, if doubly ionised).
Helium gas was puffed from a nozzle with either a 0.5 mm throat, 1 mm exit diameter (henceforth, referred to as ‘1 mm’), which gave an approximately triangular profile with side length
![]() $800~{\rm\mu}\text{m}$
, or a 1 mm throat, 2 mm exit diameter (‘2 mm’), which featured a 1 mm side length with 0.8 mm plateau. Both nozzles could produce peak molecular densities up to
$800~{\rm\mu}\text{m}$
, or a 1 mm throat, 2 mm exit diameter (‘2 mm’), which featured a 1 mm side length with 0.8 mm plateau. Both nozzles could produce peak molecular densities up to
![]() $1\times 10^{20}$
cm
$1\times 10^{20}$
cm
![]() $^{-3}$
(fully ionised,
$^{-3}$
(fully ionised,
![]() $n_{e}\leqslant 20n_{c}$
) at the laser focal position 1 mm above the nozzle exit.
$n_{e}\leqslant 20n_{c}$
) at the laser focal position 1 mm above the nozzle exit.
The blast-wave formation was measured by a transverse optical probe system, comprising a frequency doubled Nd:YAG pulse (
![]() ${\it\lambda}_{L}=532$
nm,
${\it\lambda}_{L}=532$
nm,
![]() ${\it\tau}_{L}\approx 10$
ps) split into two polarisations and differentially delayed to provide two probing times on a single shot. Each polarisation was simultaneously used for interferometry and shadowgraphy. The absolute timing between the probe pulses and the CO
${\it\tau}_{L}\approx 10$
ps) split into two polarisations and differentially delayed to provide two probing times on a single shot. Each polarisation was simultaneously used for interferometry and shadowgraphy. The absolute timing between the probe pulses and the CO
![]() $_{2}$
pulses was adjustable with an accuracy of
$_{2}$
pulses was adjustable with an accuracy of
![]() $\pm 5$
ps. The relative timing between the probe beams and main pulse was determined by imaging the rapid plasma formation resulting from the main intense pulse interacting with the gas. A Thomson spectrometer, coupled to a BC-408 polyvinyl-toluene scintillator imaged by an electron multiplying charge coupled device (EMCCD), measured the ion charge state and energy spectrum along the laser-axis.
$\pm 5$
ps. The relative timing between the probe beams and main pulse was determined by imaging the rapid plasma formation resulting from the main intense pulse interacting with the gas. A Thomson spectrometer, coupled to a BC-408 polyvinyl-toluene scintillator imaged by an electron multiplying charge coupled device (EMCCD), measured the ion charge state and energy spectrum along the laser-axis.
The prepulse energy deposition characteristics were measured by irradiating the gas target with a single
![]() ${\approx}280$
mJ pulse. Figure 4(a) shows raw interferometry data from the optical probe timed to arrive 250 ps after the initial deposition. Neutral helium gas produces negligible fringe shift compared to the plasma and was therefore ignored. The phase was extracted from interferometry (figure 4
b) and a numerical Abel inversion algorithm was used to calculate the density profile assuming cylindrical symmetry around the laser-axis (figure 4
c). A region of ionised plasma is observed with a transverse full width half maximum (FWHM)
${\approx}280$
mJ pulse. Figure 4(a) shows raw interferometry data from the optical probe timed to arrive 250 ps after the initial deposition. Neutral helium gas produces negligible fringe shift compared to the plasma and was therefore ignored. The phase was extracted from interferometry (figure 4
b) and a numerical Abel inversion algorithm was used to calculate the density profile assuming cylindrical symmetry around the laser-axis (figure 4
c). A region of ionised plasma is observed with a transverse full width half maximum (FWHM)
![]() ${\approx}100~{\rm\mu}\text{m}$
and longitudinal FWHM
${\approx}100~{\rm\mu}\text{m}$
and longitudinal FWHM
![]() ${\approx}400~{\rm\mu}\text{m}$
, similar to the measured focal spot size and Rayleigh range of the laser. A longitudinal line-out along the laser-axis is shown in figure 4(d), alongside the fully ionised gas density profile (measured in situ from neutral-gas interferometry). The target is almost fully ionised at the centre of the laser focus. The pulse has evidently deposited some of its energy in a limited region near focus. Following this initial deposition, the heated fluid expands and forms a blast wave as described in the preceding section.
${\approx}400~{\rm\mu}\text{m}$
, similar to the measured focal spot size and Rayleigh range of the laser. A longitudinal line-out along the laser-axis is shown in figure 4(d), alongside the fully ionised gas density profile (measured in situ from neutral-gas interferometry). The target is almost fully ionised at the centre of the laser focus. The pulse has evidently deposited some of its energy in a limited region near focus. Following this initial deposition, the heated fluid expands and forms a blast wave as described in the preceding section.

Figure 5. (a,b) Raw interferometry 100 ps before and 250 ps after the arrival of the intense pulse, with
![]() $E_{pp}\approx 70$
mJ onto a helium plasma with peak density
$E_{pp}\approx 70$
mJ onto a helium plasma with peak density
![]() $n_{e}=2.5n_{c}$
; (c,d) the corresponding inferred free-electron-density profile.
$n_{e}=2.5n_{c}$
; (c,d) the corresponding inferred free-electron-density profile.
As the main intense pulse arrived 25 ns after the prepulse, probe images were taken on a single shot 100 ps before and 250 ps after the intense interaction to investigate the effects of the target shaping. Interferometry data with prepulse energy
![]() $E_{pp}\approx 70$
mJ before and after irradiation of the intense pulse energy
$E_{pp}\approx 70$
mJ before and after irradiation of the intense pulse energy
![]() $E_{L}=6$
J on the 2 mm nozzle is shown in figure 5. Before the main pulse a small amount of fringe shift is visible corresponding to a cavity-shaped plasma with peak electron density
$E_{L}=6$
J on the 2 mm nozzle is shown in figure 5. Before the main pulse a small amount of fringe shift is visible corresponding to a cavity-shaped plasma with peak electron density
![]() ${\approx}0.3n_{c}$
(figure 5
c), significantly lower than the original neutral-gas density.
${\approx}0.3n_{c}$
(figure 5
c), significantly lower than the original neutral-gas density.
After the intense pulse arrives, a clear blast-wave structure is revealed in the plasma density (figure 5
d) with electron densities in the wall exceeding 3
![]() $n_{c}$
, greater than the peak unperturbed initial gas density,
$n_{c}$
, greater than the peak unperturbed initial gas density,
![]() $n_{e}\approx 2.5n_{c}$
if fully ionised. The accuracy of the density measurement is limited by asymmetry in the transverse plane, but the density in the cavity is
$n_{e}\approx 2.5n_{c}$
if fully ionised. The accuracy of the density measurement is limited by asymmetry in the transverse plane, but the density in the cavity is
![]() ${<}0.25n_{c}$
.
${<}0.25n_{c}$
.

Figure 6. (a) Flash simulation: particle density 25 ns after 50 mJ is deposited into helium puffed from the 2 mm gas target, replicating the target conditions in figure 5 (2 mm nozzle, fully ionised peak
![]() $n_{e}=2.5n_{c}$
), and (b) the estimated free-electron density. (c) laser-axis line-out of the electron density from the FLASH simulation (red, if fully ionised) and experiment (blue).
$n_{e}=2.5n_{c}$
), and (b) the estimated free-electron density. (c) laser-axis line-out of the electron density from the FLASH simulation (red, if fully ionised) and experiment (blue).
To elucidate these results, FLASH simulations were performed for the 2 mm helium target, depositing energy in a cylindrical volume of length
![]() $400~{\rm\mu}\text{m}$
and radius
$400~{\rm\mu}\text{m}$
and radius
![]() $70~{\rm\mu}\text{m}$
, similar to the size of the beam waist and Rayleigh range as well as the size of the ionised region calculated from the data in figure 4. The cylinder was centred at the laser focus position,
$70~{\rm\mu}\text{m}$
, similar to the size of the beam waist and Rayleigh range as well as the size of the ionised region calculated from the data in figure 4. The cylinder was centred at the laser focus position,
![]() $200~{\rm\mu}\text{m}$
in front of the start of the plateau region. Figure 6(a) shows the fluid particle density 25 ns after depositing
$200~{\rm\mu}\text{m}$
in front of the start of the plateau region. Figure 6(a) shows the fluid particle density 25 ns after depositing
![]() $E_{abs}=50$
mJ. A clear cavity has formed, very similar in size and shape to that seen in figure 5. Prior to the main pulse, the ionisation fraction at this point of the expansion can be estimated by assuming local thermal equilibrium and solving the Saha equation using the temperature and density output from the FLASH simulation. The resulting free-electron density is shown in figure 6. The centre of the cavity is fully ionised due to its high temperature, but the low cavity density means that the resulting phase shift would be small. Approaching the cavity wall, the temperature falls and the free-electron density rapidly drops to zero. The extent of ionisation matches closely to the experimental plasma profile prior to the intense pulse (figure 5
a,c).
$E_{abs}=50$
mJ. A clear cavity has formed, very similar in size and shape to that seen in figure 5. Prior to the main pulse, the ionisation fraction at this point of the expansion can be estimated by assuming local thermal equilibrium and solving the Saha equation using the temperature and density output from the FLASH simulation. The resulting free-electron density is shown in figure 6. The centre of the cavity is fully ionised due to its high temperature, but the low cavity density means that the resulting phase shift would be small. Approaching the cavity wall, the temperature falls and the free-electron density rapidly drops to zero. The extent of ionisation matches closely to the experimental plasma profile prior to the intense pulse (figure 5
a,c).
The blast wave therefore exists prior to the arrival of the pulse, driven by the prepulse, but is not clearly observed by interferometry due to the low ionisation fraction in the cavity wall as the relative fringe shift from an unionised gas is significantly smaller than that of a plasma of the same density. When the intense pulse arrives, a significant fraction of its energy is deposited into the target causing increased ionisation and further revealing the shock front (figure 5
b,d). Line-outs of the density profile along the laser-axis from the FLASH simulation and the experimental measurement (taken
![]() $100~{\rm\mu}\text{m}$
off-axis to avoid axial numerical effects from the Abel inversion) are shown in figure 6(c). At this stage (250 ps after the interaction), the experimentally measured density scale-length is
$100~{\rm\mu}\text{m}$
off-axis to avoid axial numerical effects from the Abel inversion) are shown in figure 6(c). At this stage (250 ps after the interaction), the experimentally measured density scale-length is
![]() $l=80~{\rm\mu}\text{m}$
, compared to
$l=80~{\rm\mu}\text{m}$
, compared to
![]() $l=60~{\rm\mu}\text{m}$
predicted by the FLASH simulation, with the densest part of the blast wave likely not to be fully ionised. The plasma will also have undergone further expansion after the intense heating by the main intense pulse. Importantly however, the density gradient that the intense laser pulse would interact with has been steepened significantly. As described previously, the scale-length can be shortened by optimising the prepulse energy, and scale-lengths down to
$l=60~{\rm\mu}\text{m}$
predicted by the FLASH simulation, with the densest part of the blast wave likely not to be fully ionised. The plasma will also have undergone further expansion after the intense heating by the main intense pulse. Importantly however, the density gradient that the intense laser pulse would interact with has been steepened significantly. As described previously, the scale-length can be shortened by optimising the prepulse energy, and scale-lengths down to
![]() $40~{\rm\mu}\text{m}$
were observed for helium (Tresca et al.
Reference Tresca, Dover, Cook, Maharjan, Polyanskiy, Najmudin, Shkolnikov and Pogorelsky2015).
$40~{\rm\mu}\text{m}$
were observed for helium (Tresca et al.
Reference Tresca, Dover, Cook, Maharjan, Polyanskiy, Najmudin, Shkolnikov and Pogorelsky2015).

Figure 7. Experimental variation of blast-wave radius 250 ps after the main pulse at fixed gas density against
![]() $E_{pp}$
, together with the analytical Sedov solution where
$E_{pp}$
, together with the analytical Sedov solution where
![]() $E_{abs}=E_{pp}$
(green dotted line), and
$E_{abs}=E_{pp}$
(green dotted line), and
![]() $E_{abs}$
modified by the absorption model (blue dotted line). The error on the laser prepulse energy measurement is estimated from noise level on the calibrated photodiode trace.
$E_{abs}$
modified by the absorption model (blue dotted line). The error on the laser prepulse energy measurement is estimated from noise level on the calibrated photodiode trace.
The effect of experimentally varying
![]() $E_{pp}$
on the transverse size of the deposition region at the point of widest expansion (corresponding to an initial density
$E_{pp}$
on the transverse size of the deposition region at the point of widest expansion (corresponding to an initial density
![]() $n_{i}\approx 0.4n_{c}$
), while keeping the target conditions constant, is shown in figure 7, measured 250 ps after the main pulse. The transverse size was measured by the location of the sharp intensity variation on shadowgraphy images which indicate the extent of the blast-wave feature. There is a gradual increase in the radius with increasing prepulse energy. If the prepulse energy was fully converted to thermal energy which drives the blast wave (i.e.
$n_{i}\approx 0.4n_{c}$
), while keeping the target conditions constant, is shown in figure 7, measured 250 ps after the main pulse. The transverse size was measured by the location of the sharp intensity variation on shadowgraphy images which indicate the extent of the blast-wave feature. There is a gradual increase in the radius with increasing prepulse energy. If the prepulse energy was fully converted to thermal energy which drives the blast wave (i.e.
![]() $E_{pp}=E_{abs}$
), the estimated radius for a spherical expansion into a isotropic gas of
$E_{pp}=E_{abs}$
), the estimated radius for a spherical expansion into a isotropic gas of
![]() $n_{i}=0.4n_{c}$
would be given by the green dotted line (2.7). Despite a cylindrical deposition of laser energy, a spherical expansion model is justified in the late stage as the longitudinal size becomes much larger than the initial deposition length. The model has limited applicability since the target is not isotropic. Nevertheless, the dependence of blast-wave radius
$n_{i}=0.4n_{c}$
would be given by the green dotted line (2.7). Despite a cylindrical deposition of laser energy, a spherical expansion model is justified in the late stage as the longitudinal size becomes much larger than the initial deposition length. The model has limited applicability since the target is not isotropic. Nevertheless, the dependence of blast-wave radius
![]() $r_{bw}$
on deposited energy
$r_{bw}$
on deposited energy
![]() $E_{abs}$
if all of the energy is assumed to be deposited in this volume would still be similar to
$E_{abs}$
if all of the energy is assumed to be deposited in this volume would still be similar to
![]() $r_{bw}\propto (E_{abs})^{0.2}$
, which poorly matches the experimental data. Including the energy-deposition model introduced in the previous section, and using the focal spot parameters (
$r_{bw}\propto (E_{abs})^{0.2}$
, which poorly matches the experimental data. Including the energy-deposition model introduced in the previous section, and using the focal spot parameters (
![]() $w_{0}=70~{\rm\mu}\text{m}$
,
$w_{0}=70~{\rm\mu}\text{m}$
,
![]() $Z_{R}=400~{\rm\mu}\text{m}$
) and
$Z_{R}=400~{\rm\mu}\text{m}$
) and
![]() $E_{pp}$
as input, (the dotted blue line) predicts a slower response to increasing prepulse energy. This is due to the energy-absorption fraction diminishing with increased laser energy, following much more closely the experimental observations.
$E_{pp}$
as input, (the dotted blue line) predicts a slower response to increasing prepulse energy. This is due to the energy-absorption fraction diminishing with increased laser energy, following much more closely the experimental observations.

Figure 8. Interferometry from 250 ps after the interaction with (a)
![]() $E_{pp}=120$
mJ and (b)
$E_{pp}=120$
mJ and (b)
![]() $E_{pp}=1.6$
J.
$E_{pp}=1.6$
J.
The effect of using prepulse energies outside the optimal range is shown in figure 8, taken using the 1 mm nozzle with a peak density
![]() $n_{i}=0.8n_{c}$
. Due to a lower density at the laser focal position the absorption fraction is smaller, and hence a larger prepulse is required to create a similarly sized cavity to that in figure 5. If the prepulse is too small, only a small cavity can form, and does not open up to the vacuum region (figure 8
a). For such a plasma, the intense pulse arrives and is adversely absorbed in the rising edge of the gas jet before the cavity, and does not interact with a steepened profile. For a very large prepulse (figure 8
b), the blast wave formed propagates too far and completely blows through the jet, so the intense pulse can only interact with a low-density remnant in the centre of the cylindrical cavity.
$n_{i}=0.8n_{c}$
. Due to a lower density at the laser focal position the absorption fraction is smaller, and hence a larger prepulse is required to create a similarly sized cavity to that in figure 5. If the prepulse is too small, only a small cavity can form, and does not open up to the vacuum region (figure 8
a). For such a plasma, the intense pulse arrives and is adversely absorbed in the rising edge of the gas jet before the cavity, and does not interact with a steepened profile. For a very large prepulse (figure 8
b), the blast wave formed propagates too far and completely blows through the jet, so the intense pulse can only interact with a low-density remnant in the centre of the cylindrical cavity.
The advantages of having a steepened density profile for ion acceleration are described in Tresca et al. (Reference Tresca, Dover, Cook, Maharjan, Polyanskiy, Najmudin, Shkolnikov and Pogorelsky2015). With no prepulse, the intense pulse was absorbed over a long scale-length and no longitudinal ion generation was observed. However, when the prepulse values were
![]() ${\approx}100{-}250$
mJ for the 1 mm nozzle and a peak
${\approx}100{-}250$
mJ for the 1 mm nozzle and a peak
![]() $n_{e}=1.6n_{c}$
, broadband helium beams were reproducibly generated with maximum observable energies up to
$n_{e}=1.6n_{c}$
, broadband helium beams were reproducibly generated with maximum observable energies up to
![]() ${\approx}1.5~\text{MeV}$
. When exceedingly large prepulses were used (
${\approx}1.5~\text{MeV}$
. When exceedingly large prepulses were used (
![]() ${>}300$
mJ), again no ion beams were observed since the density scale-length increases and eventually, as shown in figure 8(b), there is no longer an overcritical plasma for the laser to interact with. Particle-in-cell simulations confirmed that using a steepened density profile is essential to generate ion beams from collisionless electrostatic shocks.
${>}300$
mJ), again no ion beams were observed since the density scale-length increases and eventually, as shown in figure 8(b), there is no longer an overcritical plasma for the laser to interact with. Particle-in-cell simulations confirmed that using a steepened density profile is essential to generate ion beams from collisionless electrostatic shocks.
Using hydrogen as a target gas also resulted in reproducible broadband beams. However, the lower ratio of specific heat
![]() ${\it\gamma}\approx 1.4$
provides even steeper cavity walls (Sedov Reference Sedov1959) and a higher peak density (2.8). We note that the prepulse energies required to produce density profiles suitable for ion acceleration were lower for hydrogen than helium. Although increasing
${\it\gamma}\approx 1.4$
provides even steeper cavity walls (Sedov Reference Sedov1959) and a higher peak density (2.8). We note that the prepulse energies required to produce density profiles suitable for ion acceleration were lower for hydrogen than helium. Although increasing
![]() $Z$
increases plasma collisionality and hence laser absorption, a larger mass density for a given electron density results in the blast wave still expanding more slowly (2.7) even if the higher
$Z$
increases plasma collisionality and hence laser absorption, a larger mass density for a given electron density results in the blast wave still expanding more slowly (2.7) even if the higher
![]() $Z$
gas is fully ionised during breakdown. Furthermore, due to its lower binding energy hydrogen requires a lower laser intensity than helium to trigger the initial plasma breakdown, allowing for a longer heating phase (Gibbon Reference Gibbon2005). The density scale-length is minimised for a cavity just large enough to open into the vacuum, and it was found that for the steepest density profiles (
$Z$
gas is fully ionised during breakdown. Furthermore, due to its lower binding energy hydrogen requires a lower laser intensity than helium to trigger the initial plasma breakdown, allowing for a longer heating phase (Gibbon Reference Gibbon2005). The density scale-length is minimised for a cavity just large enough to open into the vacuum, and it was found that for the steepest density profiles (
![]() ${\approx}20~{\rm\mu}\text{m}$
), it was possible to generate quasi-monoenergetic beams with
${\approx}20~{\rm\mu}\text{m}$
), it was possible to generate quasi-monoenergetic beams with
![]() $E_{max}$
up to 1.4 MeV and energy spread as low as
$E_{max}$
up to 1.4 MeV and energy spread as low as
![]() ${\approx}5\,\%$
.
${\approx}5\,\%$
.
4. Discussion
The experimental data shown here and in Tresca et al. (Reference Tresca, Dover, Cook, Maharjan, Polyanskiy, Najmudin, Shkolnikov and Pogorelsky2015) were for
![]() ${\it\lambda}=10~{\rm\mu}\text{m}$
pulses, in which the required initial densities,
${\it\lambda}=10~{\rm\mu}\text{m}$
pulses, in which the required initial densities,
![]() $n_{e}\approx 10^{19}$
cm
$n_{e}\approx 10^{19}$
cm
![]() $^{-3}$
, are easily achievable from standard gas nozzles used widely in high-intensity laser–plasma interactions. However, using high-density gas jets, it would be possible to apply the same techniques to create steepened profiles which are overdense to near-infrared wavelengths (
$^{-3}$
, are easily achievable from standard gas nozzles used widely in high-intensity laser–plasma interactions. However, using high-density gas jets, it would be possible to apply the same techniques to create steepened profiles which are overdense to near-infrared wavelengths (
![]() ${\it\lambda}_{L}\approx 1~{\rm\mu}\text{m}$
). The higher collisionality results in a higher prepulse absorption efficiency,
${\it\lambda}_{L}\approx 1~{\rm\mu}\text{m}$
). The higher collisionality results in a higher prepulse absorption efficiency,
![]() ${\it\eta}$
. Despite the higher density requirements and
${\it\eta}$
. Despite the higher density requirements and
![]() $r_{bw}\propto (E_{abs}/n_{i})$
scaling, it is still possible to generate blast waves of radii of the same order as a typical sonic gas jet using
$r_{bw}\propto (E_{abs}/n_{i})$
scaling, it is still possible to generate blast waves of radii of the same order as a typical sonic gas jet using
![]() $E_{pp}<1$
J. This is shown in figure 9(a) in which the output of the numerical model (2.4) is used to estimate the blast-wave size using (2.7). Axial density profiles from FLASH simulations using a typical gas density profile from Sylla et al. (Reference Sylla, Veltcheva, Kahaly, Flacco and Malka2012) with peak hydrogen density
$E_{pp}<1$
J. This is shown in figure 9(a) in which the output of the numerical model (2.4) is used to estimate the blast-wave size using (2.7). Axial density profiles from FLASH simulations using a typical gas density profile from Sylla et al. (Reference Sylla, Veltcheva, Kahaly, Flacco and Malka2012) with peak hydrogen density
![]() $n_{i}=0.7\times 10^{21}$
cm
$n_{i}=0.7\times 10^{21}$
cm
![]() $^{3}$
are shown at various times for
$^{3}$
are shown at various times for
![]() $E_{abs}=100$
mJ deposited in a cylinder radius
$E_{abs}=100$
mJ deposited in a cylinder radius
![]() $50~{\rm\mu}\text{m}$
and length
$50~{\rm\mu}\text{m}$
and length
![]() $200~{\rm\mu}\text{m}$
, centred
$200~{\rm\mu}\text{m}$
, centred
![]() $250~{\rm\mu}\text{m}$
from peak density (figure 9
b), demonstrating density profile steepening. Furthermore, the increase in the peak density from the shockwave helps to relax the requirements on high gas-jet backing pressure for achieving
$250~{\rm\mu}\text{m}$
from peak density (figure 9
b), demonstrating density profile steepening. Furthermore, the increase in the peak density from the shockwave helps to relax the requirements on high gas-jet backing pressure for achieving
![]() $n_{e}>n_{cr}$
, as necessitated for an opaque target.
$n_{e}>n_{cr}$
, as necessitated for an opaque target.

Figure 9. (a) Example blast-wave radii achievable for different
![]() $E_{abs}$
after 5 ns expansion with
$E_{abs}$
after 5 ns expansion with
![]() ${\it\lambda}_{L}=1~{\rm\mu}\text{m}$
,
${\it\lambda}_{L}=1~{\rm\mu}\text{m}$
,
![]() ${\it\tau}_{L}=5$
ps,
${\it\tau}_{L}=5$
ps,
![]() $w_{0}\approx 50~{\rm\mu}\text{m}$
heating a volume length
$w_{0}\approx 50~{\rm\mu}\text{m}$
heating a volume length
![]() $300~{\rm\mu}\text{m}$
in an initially uniform plasma (solid, left
$300~{\rm\mu}\text{m}$
in an initially uniform plasma (solid, left
![]() $y$
-axis), and the corresponding absorption fraction (dotted, right
$y$
-axis), and the corresponding absorption fraction (dotted, right
![]() $y$
-axis). (b) Axial density profiles at different times from FLASH simulations of blast waves generated in a high-density gas jet.
$y$
-axis). (b) Axial density profiles at different times from FLASH simulations of blast waves generated in a high-density gas jet.
We have therefore demonstrated all-optical tailoring of gas-jet profiles of interest to longitudinal radiation pressure driven ion acceleration mechanisms. By carefully choosing an appropriate prepulse, we have driven hydrodynamic blast waves to produce targets with significantly steeper density gradients than a typical gas jet. This scheme has been successfully used to generate longitudinal ion beams via collisionless shock acceleration (Tresca et al. Reference Tresca, Dover, Cook, Maharjan, Polyanskiy, Najmudin, Shkolnikov and Pogorelsky2015), and opens up new possibilities for intense laser interactions with near-critical density targets.
Acknowledgements
This work was supported by the US DOE grant DE-FG02- 07ER41488, UK EPSRC grant EP/K022415/1 and STFC grant ST/J002062/1. FLASH was developed by the DOE NNSA ASC and NSF-supported FCCS at the University of Chicago. EPOCH development was supported by EPSRC grants EP/G054940/1, EP/G055165/1 and EP/G056803/1. Computing resources were provided by Imperial College HPC services.