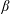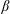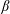1 Introduction
Magnetic reconnection is the process by which magnetic energy is converted to plasma energy via a rapid topological rearrangement of magnetic-field lines (Zweibel & Yamada Reference Zweibel and Yamada2009; Yamada, Kulsrud & Ji Reference Yamada, Kulsrud and Ji2010; Loureiro & Uzdensky Reference Loureiro and Uzdensky2016). It is usually preceded by a slow phase in which magnetic flux is accumulated in an increasingly thin current sheet (CS). Recently, it has been conjectured that this preparatory phase of CS formation, along with the material properties of the host plasma, determine the characteristics of the tearing modes that ultimately disrupt the sheet and thereby set the maximum aspect ratio above which CSs cannot survive (Pucci & Velli Reference Pucci and Velli2014; Tenerani et al. Reference Tenerani, Velli, Rappazzo and Pucci2015; Loureiro & Uzdensky Reference Loureiro and Uzdensky2016; Uzdensky & Loureiro Reference Uzdensky and Loureiro2016; Comisso et al. Reference Comisso, Lingam, Huang and Bhattacharjee2017; Huang, Comisso & Bhattacharjee Reference Huang, Comisso and Bhattacharjee2017). This maximum aspect ratio is important for (at least) two reasons. First, the large aspect ratio of the Sweet–Parker CS (Parker Reference Parker1957; Sweet Reference Sweet and Lehnert1958) in high-Lundquist-number plasmas, being violently unstable to the plasmoid instability (Loureiro, Schekochihin & Cowley Reference Loureiro, Schekochihin and Cowley2007; Bhattacharjee et al. Reference Bhattacharjee, Huang, Yang and Rogers2009), may not be realizable during CS formation. Second, the maximum aspect ratio may define a disruption scale in critically balanced Alfvénic turbulence, below which the intense, sheet-like structures become tearing unstable and break up (Boldyrev & Loureiro Reference Boldyrev and Loureiro2017; Loureiro & Boldyrev Reference Loureiro and Boldyrev2017a ,Reference Loureiro and Boldyrev b ; Mallet, Schekochihin & Chandran Reference Mallet, Schekochihin and Chandran2017a ,Reference Mallet, Schekochihin and Chandran b ).
All of the work thus far on CS formation and tearing-mediated disruption was either couched within a collisional magnetohydrodynamic (MHD) framework or focused on collisionless plasmas with
![]() $\unicode[STIX]{x1D6FD}\doteq 8\unicode[STIX]{x03C0}nT/B^{2}\lesssim 1$
(
$\unicode[STIX]{x1D6FD}\doteq 8\unicode[STIX]{x03C0}nT/B^{2}\lesssim 1$
(
![]() $n$
is the plasma density,
$n$
is the plasma density,
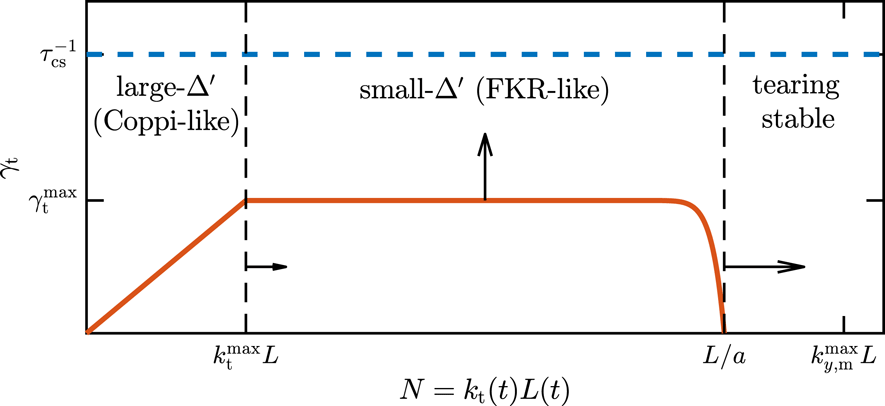
![]() $T$
the temperature and
$T$
the temperature and
![]() $B$
the magnetic-field strength). The latter restriction precludes application of those results to many dilute, weakly collisional astrophysical plasmas, whose large temperatures and relatively weak magnetic fields imply
$B$
the magnetic-field strength). The latter restriction precludes application of those results to many dilute, weakly collisional astrophysical plasmas, whose large temperatures and relatively weak magnetic fields imply
![]() $\unicode[STIX]{x1D6FD}\gg 1$
. For example,
$\unicode[STIX]{x1D6FD}\gg 1$
. For example,
![]() $n\sim 10^{-3}~\text{cm}^{-3}$
,
$n\sim 10^{-3}~\text{cm}^{-3}$
,
![]() $T\sim 5~\text{keV}$
and
$T\sim 5~\text{keV}$
and
![]() $B\sim 1~\unicode[STIX]{x03BC}\text{G}$
in the hot intracluster medium (ICM) of galaxy clusters imply
$B\sim 1~\unicode[STIX]{x03BC}\text{G}$
in the hot intracluster medium (ICM) of galaxy clusters imply
![]() $\unicode[STIX]{x1D6FD}\sim 10^{2}$
(Carilli & Taylor Reference Carilli and Taylor2002; Schekochihin & Cowley Reference Schekochihin and Cowley2006);
$\unicode[STIX]{x1D6FD}\sim 10^{2}$
(Carilli & Taylor Reference Carilli and Taylor2002; Schekochihin & Cowley Reference Schekochihin and Cowley2006);
![]() $n\sim 100~\text{cm}^{-3}$
,
$n\sim 100~\text{cm}^{-3}$
,
![]() $T\sim 2~\text{keV}$
and
$T\sim 2~\text{keV}$
and
![]() $B\sim 1~\text{mG}$
near the accretion radius of Sgr A
$B\sim 1~\text{mG}$
near the accretion radius of Sgr A
![]() $^{\ast }$
at the Galactic centre imply
$^{\ast }$
at the Galactic centre imply
![]() $\unicode[STIX]{x1D6FD}\sim 10$
(Quataert Reference Quataert2003; Marrone, Moran, Zhao & Rao Reference Marrone, Moran, Zhao and Rao2007). The hallmark of such plasmas is that the embedded magnetic field, while energetically subdominant, nevertheless has a strength tens of orders of magnitude above that required to magnetize the plasma (i.e.
$\unicode[STIX]{x1D6FD}\sim 10$
(Quataert Reference Quataert2003; Marrone, Moran, Zhao & Rao Reference Marrone, Moran, Zhao and Rao2007). The hallmark of such plasmas is that the embedded magnetic field, while energetically subdominant, nevertheless has a strength tens of orders of magnitude above that required to magnetize the plasma (i.e.
![]() $\unicode[STIX]{x1D6FA}_{i}\unicode[STIX]{x1D70F}\ggg 1$
and
$\unicode[STIX]{x1D6FA}_{i}\unicode[STIX]{x1D70F}\ggg 1$
and
![]() $\unicode[STIX]{x1D70C}_{i}\lll L$
, where
$\unicode[STIX]{x1D70C}_{i}\lll L$
, where
![]() $\unicode[STIX]{x1D6FA}_{i}\doteq eB/m_{i}c$
is the ion-Larmor frequency,
$\unicode[STIX]{x1D6FA}_{i}\doteq eB/m_{i}c$
is the ion-Larmor frequency,
![]() $m_{i}$
is the ion mass,
$m_{i}$
is the ion mass,
![]() $\unicode[STIX]{x1D70C}_{i}\doteq v_{\text{th}i}/\unicode[STIX]{x1D6FA}_{i}$
is the ion-Larmor radius,
$\unicode[STIX]{x1D70C}_{i}\doteq v_{\text{th}i}/\unicode[STIX]{x1D6FA}_{i}$
is the ion-Larmor radius,
![]() $v_{\text{th}i}\doteq (2T/m_{i})^{1/2}$
is the ion thermal speed and
$v_{\text{th}i}\doteq (2T/m_{i})^{1/2}$
is the ion thermal speed and
![]() $\unicode[STIX]{x1D70F}$
and
$\unicode[STIX]{x1D70F}$
and
![]() $L$
are representative macroscopic time and length scales, respectively). This hierarchy of scales, particularly in weakly collisional plasmas with collision frequencies
$L$
are representative macroscopic time and length scales, respectively). This hierarchy of scales, particularly in weakly collisional plasmas with collision frequencies
![]() $\unicode[STIX]{x1D708}$
satisfying
$\unicode[STIX]{x1D708}$
satisfying
![]() $\unicode[STIX]{x1D708}\unicode[STIX]{x1D70F}\ll 1$
, biases the plasma properties with respect to the magnetic-field direction (Braginskii Reference Braginskii1965). Notably, the thermal pressure becomes anisotropic.
$\unicode[STIX]{x1D708}\unicode[STIX]{x1D70F}\ll 1$
, biases the plasma properties with respect to the magnetic-field direction (Braginskii Reference Braginskii1965). Notably, the thermal pressure becomes anisotropic.
There is a relatively large body of work on the impact of pressure anisotropy on tearing modes (Chen & Davidson Reference Chen and Davidson1981; Coppi Reference Coppi1983; Chen & Palmadesso Reference Chen and Palmadesso1984; Chen & Lee Reference Chen and Lee1985; Ambrosiano, Lee & Fu Reference Ambrosiano, Lee and Fu1986; Shi, Lee & Fu Reference Shi, Lee and Fu1987; Karimabadi, Daughton & Quest Reference Karimabadi, Daughton and Quest2005; Haijima et al.
Reference Haijima, Tanaka, Fujimoto and Shinohara2008; Quest, Karimabadi & Daughton Reference Quest, Karimabadi and Daughton2010; Matteini et al.
Reference Matteini, Landi, Velli and Matthaeus2013; Gingell, Burgess & Matteini Reference Gingell, Burgess and Matteini2015), as well as on the production and impact of pressure anisotropy during the reconnection process itself (Drake et al.
Reference Drake, Swisdak, Che and Shay2006; Le et al.
Reference Le, Egedal, Daughton, Fox and Katz2009; Schoeffler, Drake & Swisdak Reference Schoeffler, Drake and Swisdak2011; Egedal, Le & Daughton Reference Egedal, Le and Daughton2013; Cassak et al.
Reference Cassak, Baylor, Fermo, Beidler, Shay, Swisdak, Drake and Karimabadi2015; Le et al.
Reference Le, Daughton, Karimabadi and Egedal2016). Here we focus instead on the pressure anisotropy adiabatically produced during the CS formation, prior to the reconnection event. Namely, as the CS thins, the magnetic-field strength in the inflowing fluid elements increases. An increase in field strength in a weakly collisional, magnetized plasma leads, by adiabatic invariance, to an increase (decrease) in the thermal pressure perpendicular (parallel) to the field lines (Chew, Goldberger & Low Reference Chew, Goldberger and Low1956). Above an
![]() $O(1/\unicode[STIX]{x1D6FD})$
threshold, this pressure anisotropy drives the mirror instability (Barnes Reference Barnes1966; Hasegawa Reference Hasegawa1969; Southwood & Kivelson Reference Southwood and Kivelson1993), which produces strong distortions in the field lines and traps particles on ion-Larmor scales (Kunz, Schekochihin & Stone Reference Kunz, Schekochihin and Stone2014; Riquelme, Quataert & Verscharen Reference Riquelme, Quataert and Verscharen2015). In what follows, we ask how the production of pressure anisotropy during CS formation and the consequent triggering of ion-Larmor-scale mirror instabilities in a
$O(1/\unicode[STIX]{x1D6FD})$
threshold, this pressure anisotropy drives the mirror instability (Barnes Reference Barnes1966; Hasegawa Reference Hasegawa1969; Southwood & Kivelson Reference Southwood and Kivelson1993), which produces strong distortions in the field lines and traps particles on ion-Larmor scales (Kunz, Schekochihin & Stone Reference Kunz, Schekochihin and Stone2014; Riquelme, Quataert & Verscharen Reference Riquelme, Quataert and Verscharen2015). In what follows, we ask how the production of pressure anisotropy during CS formation and the consequent triggering of ion-Larmor-scale mirror instabilities in a
![]() $\unicode[STIX]{x1D6FD}\gg 1$
plasma impacts the onset of tearing-mediated reconnection.
$\unicode[STIX]{x1D6FD}\gg 1$
plasma impacts the onset of tearing-mediated reconnection.
2 Prerequisites
2.1 CS formation and pressure anisotropy
We first establish that pressure anisotropy is produced during CS formation. For that, we adopt a simple local model for CS formation based on a one-dimensional generalization of the Chapman–Kendall solution (Chapman & Kendall Reference Chapman and Kendall1963; Tolman, Loureiro & Uzdensky Reference Tolman, Loureiro and Uzdensky2018, §2). A sheared magnetic field
![]() $\boldsymbol{B}(x,\!t)=B_{\text{r}}[x/a(t)]\,\hat{\boldsymbol{y}}+B_{\text{g}}\hat{\boldsymbol{z}}$
is frozen into an incompressible, time-independent fluid velocity
$\boldsymbol{B}(x,\!t)=B_{\text{r}}[x/a(t)]\,\hat{\boldsymbol{y}}+B_{\text{g}}\hat{\boldsymbol{z}}$
is frozen into an incompressible, time-independent fluid velocity
![]() $\boldsymbol{u}(x,\!y)=-(x\hat{\boldsymbol{x}}-y\hat{\boldsymbol{y}})/2\unicode[STIX]{x1D70F}_{\text{cs}}$
, where
$\boldsymbol{u}(x,\!y)=-(x\hat{\boldsymbol{x}}-y\hat{\boldsymbol{y}})/2\unicode[STIX]{x1D70F}_{\text{cs}}$
, where
![]() $B_{\text{r}}$
and
$B_{\text{r}}$
and
![]() $B_{\text{g}}\doteq \unicode[STIX]{x1D703}B_{\text{r}}$
are constants describing the strengths of the reconnecting and guide components of
$B_{\text{g}}\doteq \unicode[STIX]{x1D703}B_{\text{r}}$
are constants describing the strengths of the reconnecting and guide components of
![]() $\boldsymbol{B}$
, respectively, and
$\boldsymbol{B}$
, respectively, and
![]() $\unicode[STIX]{x1D70F}_{\text{cs}}$
is the characteristic CS-formation time scale. These expressions satisfy the reduced MHD equations provided that the CS half-thickness
$\unicode[STIX]{x1D70F}_{\text{cs}}$
is the characteristic CS-formation time scale. These expressions satisfy the reduced MHD equations provided that the CS half-thickness
![]() $a(t)$
and length
$a(t)$
and length
![]() $L(t)$
satisfy
$L(t)$
satisfy
![]() $a(t)/a_{0}=L_{0}/L(t)=\exp (-t/\unicode[STIX]{x1D70F}_{\text{cs}})$
, where the ‘
$a(t)/a_{0}=L_{0}/L(t)=\exp (-t/\unicode[STIX]{x1D70F}_{\text{cs}})$
, where the ‘
![]() $0$
’ subscript denotes an initial value. This model may be regarded as a Taylor expansion about the neutral line (
$0$
’ subscript denotes an initial value. This model may be regarded as a Taylor expansion about the neutral line (
![]() $x=0$
) of a more complicated (e.g. Harris) CS profile, and so we restrict its validity to
$x=0$
) of a more complicated (e.g. Harris) CS profile, and so we restrict its validity to
![]() $|y|\ll L(t)$
and
$|y|\ll L(t)$
and
![]() $|x|\lesssim a(t)$
, beyond which
$|x|\lesssim a(t)$
, beyond which
![]() $\boldsymbol{B}$
is taken to be spatio-temporally constant. (Indeed, this simple model is only meant to illustrate that
$\boldsymbol{B}$
is taken to be spatio-temporally constant. (Indeed, this simple model is only meant to illustrate that
![]() $\unicode[STIX]{x1D6E5}_{p}>0$
can be driven during CS formation.) We assume
$\unicode[STIX]{x1D6E5}_{p}>0$
can be driven during CS formation.) We assume
![]() $\sqrt{\unicode[STIX]{x1D70C}_{i,\text{r}}/a}\ll \unicode[STIX]{x1D703}\lesssim 1$
and
$\sqrt{\unicode[STIX]{x1D70C}_{i,\text{r}}/a}\ll \unicode[STIX]{x1D703}\lesssim 1$
and
![]() $\unicode[STIX]{x1D6FA}_{i}\unicode[STIX]{x1D70F}_{\text{cs}}\gg 1$
, where
$\unicode[STIX]{x1D6FA}_{i}\unicode[STIX]{x1D70F}_{\text{cs}}\gg 1$
, where
![]() $\unicode[STIX]{x1D70C}_{i,\text{r}}$
is the ion-Larmor radius computed using
$\unicode[STIX]{x1D70C}_{i,\text{r}}$
is the ion-Larmor radius computed using
![]() $B_{\text{r}}$
, so that the entire CS is well magnetized (even near
$B_{\text{r}}$
, so that the entire CS is well magnetized (even near
![]() $x=0$
).Footnote
1
$x=0$
).Footnote
1
Using these fields, it is straightforward to show that the magnetic-field strength in a fluid element starting at
![]() $x=\unicode[STIX]{x1D709}_{0}$
(with
$x=\unicode[STIX]{x1D709}_{0}$
(with
![]() $|\unicode[STIX]{x1D709}_{0}|\leqslant a_{0}$
) and moving towards
$|\unicode[STIX]{x1D709}_{0}|\leqslant a_{0}$
) and moving towards
![]() $x=0$
is
$x=0$
is
where
![]() $\unicode[STIX]{x1D709}(t)=\unicode[STIX]{x1D709}_{0}\exp (-t/2\unicode[STIX]{x1D70F}_{\text{cs}})$
is a Lagrangian coordinate co-moving with the fluid element. This change in
$\unicode[STIX]{x1D709}(t)=\unicode[STIX]{x1D709}_{0}\exp (-t/2\unicode[STIX]{x1D70F}_{\text{cs}})$
is a Lagrangian coordinate co-moving with the fluid element. This change in
![]() $B$
drives field-aligned pressure anisotropy,
$B$
drives field-aligned pressure anisotropy,
![]() $\unicode[STIX]{x1D6E5}_{p}\doteq p_{\bot }/p_{\Vert }-1$
, adiabatically in the fluid frame. Using
$\unicode[STIX]{x1D6E5}_{p}\doteq p_{\bot }/p_{\Vert }-1$
, adiabatically in the fluid frame. Using
![]() $\unicode[STIX]{x1D707}$
conservation in the form
$\unicode[STIX]{x1D707}$
conservation in the form
![]() $p_{\bot }\propto B$
and assuming
$p_{\bot }\propto B$
and assuming
![]() $\unicode[STIX]{x1D6E5}_{p}(x,t=0)=0$
,
$\unicode[STIX]{x1D6E5}_{p}(x,t=0)=0$
,
for
![]() $t/\unicode[STIX]{x1D70F}_{\text{cs}}\ll 1$
.Footnote
2
Thus, pressure anisotropy increases in all fluid elements.
$t/\unicode[STIX]{x1D70F}_{\text{cs}}\ll 1$
.Footnote
2
Thus, pressure anisotropy increases in all fluid elements.
If nothing interferes with the adiabatic increase in pressure anisotropy, the plasma in a fluid element will eventually become mirror unstable when
![]() $\unicode[STIX]{x1D6E5}_{p}\gtrsim 1/\unicode[STIX]{x1D6FD}_{\bot }$
, where
$\unicode[STIX]{x1D6E5}_{p}\gtrsim 1/\unicode[STIX]{x1D6FD}_{\bot }$
, where
is the adiabatically evolving perpendicular plasma
![]() $\unicode[STIX]{x1D6FD}$
in the fluid frame (
$\unicode[STIX]{x1D6FD}$
in the fluid frame (
![]() $\unicode[STIX]{x1D6FD}_{0}$
is its initial value). Comparing (2.2) and (2.3), this occurs at
$\unicode[STIX]{x1D6FD}_{0}$
is its initial value). Comparing (2.2) and (2.3), this occurs at
![]() $t_{\text{m}}\sim \unicode[STIX]{x1D70F}_{\text{pa}}/\unicode[STIX]{x1D6FD}_{0}$
for
$t_{\text{m}}\sim \unicode[STIX]{x1D70F}_{\text{pa}}/\unicode[STIX]{x1D6FD}_{0}$
for
![]() $\unicode[STIX]{x1D6FD}_{0}\gg 1$
. If the guide field is small compared to the local reconnecting field (
$\unicode[STIX]{x1D6FD}_{0}\gg 1$
. If the guide field is small compared to the local reconnecting field (
![]() $\unicode[STIX]{x1D703}\ll \unicode[STIX]{x1D709}_{0}/a_{0}$
), this time is a small fraction of the CS-formation time scale,
$\unicode[STIX]{x1D703}\ll \unicode[STIX]{x1D709}_{0}/a_{0}$
), this time is a small fraction of the CS-formation time scale,
![]() $t_{\text{m}}\sim \unicode[STIX]{x1D70F}_{\text{cs}}/\unicode[STIX]{x1D6FD}_{0}$
, and so the CS becomes mirror unstable early in its evolution. With a larger guide field (
$t_{\text{m}}\sim \unicode[STIX]{x1D70F}_{\text{cs}}/\unicode[STIX]{x1D6FD}_{0}$
, and so the CS becomes mirror unstable early in its evolution. With a larger guide field (
![]() $\unicode[STIX]{x1D703}\gg \unicode[STIX]{x1D709}_{0}/a_{0}$
),
$\unicode[STIX]{x1D703}\gg \unicode[STIX]{x1D709}_{0}/a_{0}$
),
![]() $t_{\text{m}}\sim \unicode[STIX]{x1D70F}_{\text{cs}}(a_{0}^{2}/\unicode[STIX]{x1D709}_{0}^{2})(\unicode[STIX]{x1D703}^{2}/\unicode[STIX]{x1D6FD}_{0})$
. This time is also early in the CS evolution for
$t_{\text{m}}\sim \unicode[STIX]{x1D70F}_{\text{cs}}(a_{0}^{2}/\unicode[STIX]{x1D709}_{0}^{2})(\unicode[STIX]{x1D703}^{2}/\unicode[STIX]{x1D6FD}_{0})$
. This time is also early in the CS evolution for
![]() $\unicode[STIX]{x1D709}_{0}\lesssim a_{0}$
, since
$\unicode[STIX]{x1D709}_{0}\lesssim a_{0}$
, since
![]() $\unicode[STIX]{x1D703}\ll \unicode[STIX]{x1D6FD}^{1/2}$
is required in this model for the plasma to reliably exceed the mirror-instability threshold.Footnote
3
$\unicode[STIX]{x1D703}\ll \unicode[STIX]{x1D6FD}^{1/2}$
is required in this model for the plasma to reliably exceed the mirror-instability threshold.Footnote
3
These times must be compared to the characteristic time scales for tearing modes that facilitate magnetic reconnection in the forming CS. Before doing so, we review the basic properties of the mirror instability.
2.2 Mirror instability
As
![]() $B$
increases, adiabatic invariance drives
$B$
increases, adiabatic invariance drives
![]() $\unicode[STIX]{x1D6E5}_{p}>0$
, with plasma becoming mirror unstable when
$\unicode[STIX]{x1D6E5}_{p}>0$
, with plasma becoming mirror unstable when
![]() $\unicode[STIX]{x1D6EC}_{\text{m}}\doteq \unicode[STIX]{x1D6E5}_{p}-1/\unicode[STIX]{x1D6FD}_{\bot }>0$
. Just beyond this threshold (
$\unicode[STIX]{x1D6EC}_{\text{m}}\doteq \unicode[STIX]{x1D6E5}_{p}-1/\unicode[STIX]{x1D6FD}_{\bot }>0$
. Just beyond this threshold (
![]() $0<\unicode[STIX]{x1D6EC}_{\text{m}}\ll 1$
), oblique modes with wavenumbers
$0<\unicode[STIX]{x1D6EC}_{\text{m}}\ll 1$
), oblique modes with wavenumbers
![]() $k_{\Vert ,\text{m}}\unicode[STIX]{x1D70C}_{i}\sim (k_{\bot ,\text{m}}\unicode[STIX]{x1D70C}_{i})^{2}\sim \unicode[STIX]{x1D6EC}_{\text{m}}$
and polarization
$k_{\Vert ,\text{m}}\unicode[STIX]{x1D70C}_{i}\sim (k_{\bot ,\text{m}}\unicode[STIX]{x1D70C}_{i})^{2}\sim \unicode[STIX]{x1D6EC}_{\text{m}}$
and polarization
![]() $\unicode[STIX]{x1D6FF}B_{\bot }/\unicode[STIX]{x1D6FF}B_{\Vert }\sim \unicode[STIX]{x1D6EC}_{\text{m}}^{1/2}$
grow exponentially at a maximum rate
$\unicode[STIX]{x1D6FF}B_{\bot }/\unicode[STIX]{x1D6FF}B_{\Vert }\sim \unicode[STIX]{x1D6EC}_{\text{m}}^{1/2}$
grow exponentially at a maximum rate
![]() $\unicode[STIX]{x1D6FE}_{\text{m}}\sim \unicode[STIX]{x1D6FA}_{i}\unicode[STIX]{x1D6EC}_{\text{m}}^{2}$
(Hellinger Reference Hellinger2007). Once this growth rate becomes larger than the rate at which
$\unicode[STIX]{x1D6FE}_{\text{m}}\sim \unicode[STIX]{x1D6FA}_{i}\unicode[STIX]{x1D6EC}_{\text{m}}^{2}$
(Hellinger Reference Hellinger2007). Once this growth rate becomes larger than the rate at which
![]() $\unicode[STIX]{x1D6E5}_{p}$
is produced (
$\unicode[STIX]{x1D6E5}_{p}$
is produced (
![]() $\unicode[STIX]{x1D6FE}_{\text{m}}\unicode[STIX]{x1D70F}_{\text{pa}}\gtrsim 1$
), the growth of
$\unicode[STIX]{x1D6FE}_{\text{m}}\unicode[STIX]{x1D70F}_{\text{pa}}\gtrsim 1$
), the growth of
![]() $\unicode[STIX]{x1D6E5}_{p}$
stops. This yields a maximum mirror-instability parameter,
$\unicode[STIX]{x1D6E5}_{p}$
stops. This yields a maximum mirror-instability parameter,
![]() $\unicode[STIX]{x1D6EC}_{\text{m}}\gtrsim (\unicode[STIX]{x1D6FA}_{i}\unicode[STIX]{x1D70F}_{\text{pa}})^{-1/2}\doteq \unicode[STIX]{x1D6EC}_{\text{m,max}}$
. Kinetic simulations show that, once
$\unicode[STIX]{x1D6EC}_{\text{m}}\gtrsim (\unicode[STIX]{x1D6FA}_{i}\unicode[STIX]{x1D70F}_{\text{pa}})^{-1/2}\doteq \unicode[STIX]{x1D6EC}_{\text{m,max}}$
. Kinetic simulations show that, once
![]() $\unicode[STIX]{x1D6EC}_{\text{m}}(t)\sim \unicode[STIX]{x1D6EC}_{\text{m,max}}$
, mirrors rapidly drain
$\unicode[STIX]{x1D6EC}_{\text{m}}(t)\sim \unicode[STIX]{x1D6EC}_{\text{m,max}}$
, mirrors rapidly drain
![]() $\unicode[STIX]{x1D6EC}_{\text{m}}(t)\rightarrow 0^{+}$
and attain amplitudes
$\unicode[STIX]{x1D6EC}_{\text{m}}(t)\rightarrow 0^{+}$
and attain amplitudes
![]() $\unicode[STIX]{x1D6FF}B_{\Vert }/B\sim \unicode[STIX]{x1D6EC}_{\text{m,max}}^{1/2}$
(Kunz et al.
Reference Kunz, Schekochihin and Stone2014). This is the end of the linear stage; for
$\unicode[STIX]{x1D6FF}B_{\Vert }/B\sim \unicode[STIX]{x1D6EC}_{\text{m,max}}^{1/2}$
(Kunz et al.
Reference Kunz, Schekochihin and Stone2014). This is the end of the linear stage; for
![]() $\unicode[STIX]{x1D6FD}_{0}\gg 1$
, this occurs at
$\unicode[STIX]{x1D6FD}_{0}\gg 1$
, this occurs at
![]() $t/\unicode[STIX]{x1D70F}_{\text{pa}}\sim 1/\unicode[STIX]{x1D6FD}_{0}+\unicode[STIX]{x1D6EC}_{\text{m,max}}$
.
$t/\unicode[STIX]{x1D70F}_{\text{pa}}\sim 1/\unicode[STIX]{x1D6FD}_{0}+\unicode[STIX]{x1D6EC}_{\text{m,max}}$
.
As the CS continues to thin,
![]() $\unicode[STIX]{x1D6E5}_{p}>0$
is continuously driven. Mirror modes then maintain marginal stability (
$\unicode[STIX]{x1D6E5}_{p}>0$
is continuously driven. Mirror modes then maintain marginal stability (
![]() $\unicode[STIX]{x1D6EC}_{\text{m}}\simeq 0^{+}$
) by growing secularly,
$\unicode[STIX]{x1D6EC}_{\text{m}}\simeq 0^{+}$
) by growing secularly,
![]() $\unicode[STIX]{x1D6FF}B_{\Vert }^{2}\propto t^{4/3}$
, and trapping an increasing fraction of particles (Schekochihin et al.
Reference Schekochihin, Cowley, Kulsrud, Rosin and Heinemann2008; Kunz et al.
Reference Kunz, Schekochihin and Stone2014; Rincon, Schekochihin & Cowley Reference Rincon, Schekochihin and Cowley2015). Independent of
$\unicode[STIX]{x1D6FF}B_{\Vert }^{2}\propto t^{4/3}$
, and trapping an increasing fraction of particles (Schekochihin et al.
Reference Schekochihin, Cowley, Kulsrud, Rosin and Heinemann2008; Kunz et al.
Reference Kunz, Schekochihin and Stone2014; Rincon, Schekochihin & Cowley Reference Rincon, Schekochihin and Cowley2015). Independent of
![]() $\unicode[STIX]{x1D6EC}_{\text{m,max}}$
, saturation occurs at
$\unicode[STIX]{x1D6EC}_{\text{m,max}}$
, saturation occurs at
![]() $t\sim \unicode[STIX]{x1D70F}_{\text{pa}}$
and
$t\sim \unicode[STIX]{x1D70F}_{\text{pa}}$
and
![]() $\unicode[STIX]{x1D6FF}B/B\sim 1$
, when these particles pitch-angle scatter off sharp bends in the magnetic field occurring at the mirror boundaries at a rate
$\unicode[STIX]{x1D6FF}B/B\sim 1$
, when these particles pitch-angle scatter off sharp bends in the magnetic field occurring at the mirror boundaries at a rate
![]() $\unicode[STIX]{x1D708}_{\text{m}}\sim \unicode[STIX]{x1D6FD}/\unicode[STIX]{x1D70F}_{\text{pa}}$
; this maintains marginal stability by severing the adiabatic link between
$\unicode[STIX]{x1D708}_{\text{m}}\sim \unicode[STIX]{x1D6FD}/\unicode[STIX]{x1D70F}_{\text{pa}}$
; this maintains marginal stability by severing the adiabatic link between
![]() $\unicode[STIX]{x1D6E5}_{p}$
and changes in
$\unicode[STIX]{x1D6E5}_{p}$
and changes in
![]() $B$
(Kunz et al.
Reference Kunz, Schekochihin and Stone2014; Riquelme et al.
Reference Riquelme, Quataert and Verscharen2015). Thereafter,
$B$
(Kunz et al.
Reference Kunz, Schekochihin and Stone2014; Riquelme et al.
Reference Riquelme, Quataert and Verscharen2015). Thereafter,
![]() $\unicode[STIX]{x1D6E5}_{p}\simeq 1/\unicode[STIX]{x1D6FD}_{\bot }$
, even as
$\unicode[STIX]{x1D6E5}_{p}\simeq 1/\unicode[STIX]{x1D6FD}_{\bot }$
, even as
![]() $B$
changes.
$B$
changes.
This evolution was found for situations in which
![]() $\unicode[STIX]{x1D70F}_{\text{pa}}$
is comparable to the dynamical time in the system (e.g. linear shear flows). However, for locations
$\unicode[STIX]{x1D70F}_{\text{pa}}$
is comparable to the dynamical time in the system (e.g. linear shear flows). However, for locations
![]() $\unicode[STIX]{x1D709}_{0}\ll \unicode[STIX]{x1D703}a_{0}$
deep inside the CS,
$\unicode[STIX]{x1D709}_{0}\ll \unicode[STIX]{x1D703}a_{0}$
deep inside the CS,
![]() $\unicode[STIX]{x1D70F}_{\text{pa}}\gg \unicode[STIX]{x1D70F}_{\text{cs}}$
. In this case, local mirror growth cannot outpace CS formation, and any potential mirrors are advected and distorted faster than they can grow. When
$\unicode[STIX]{x1D70F}_{\text{pa}}\gg \unicode[STIX]{x1D70F}_{\text{cs}}$
. In this case, local mirror growth cannot outpace CS formation, and any potential mirrors are advected and distorted faster than they can grow. When
![]() $\unicode[STIX]{x1D703}\gg 1$
,
$\unicode[STIX]{x1D703}\gg 1$
,
![]() $\unicode[STIX]{x1D70F}_{\text{pa}}\gg \unicode[STIX]{x1D70F}_{\text{cs}}$
in the entire CS. We thus focus only on cases with
$\unicode[STIX]{x1D70F}_{\text{pa}}\gg \unicode[STIX]{x1D70F}_{\text{cs}}$
in the entire CS. We thus focus only on cases with
![]() $\unicode[STIX]{x1D703}\lesssim 1$
and locations
$\unicode[STIX]{x1D703}\lesssim 1$
and locations
![]() $\unicode[STIX]{x1D709}_{0}\gtrsim \unicode[STIX]{x1D703}a_{0}$
.
$\unicode[STIX]{x1D709}_{0}\gtrsim \unicode[STIX]{x1D703}a_{0}$
.
2.3 Collisionless tearing instability
Next we review the theory of collisionless tearing modes, applicable when the inner-layer thickness of the tearing CS,
![]() $\unicode[STIX]{x1D6FF}_{\text{in}}\lesssim \unicode[STIX]{x1D70C}_{e}$
. To determine under what condition this criterion is satisfied, we use standard MHD tearing theory (Furth, Killeen & Rosenbluth Reference Furth, Killeen and Rosenbluth1963; FKR) to estimate
$\unicode[STIX]{x1D6FF}_{\text{in}}\lesssim \unicode[STIX]{x1D70C}_{e}$
. To determine under what condition this criterion is satisfied, we use standard MHD tearing theory (Furth, Killeen & Rosenbluth Reference Furth, Killeen and Rosenbluth1963; FKR) to estimate
where
![]() $v_{\text{A,r}}\doteq B_{\text{r}}/(4\unicode[STIX]{x03C0}m_{i}n_{i})^{1/2}$
is the Alfvén speed of the reconnecting field,
$v_{\text{A,r}}\doteq B_{\text{r}}/(4\unicode[STIX]{x03C0}m_{i}n_{i})^{1/2}$
is the Alfvén speed of the reconnecting field,
![]() $\unicode[STIX]{x1D70F}_{\text{A,r}}\doteq a/v_{\text{A,r}}$
is the Alfvén crossing time of the CS,
$\unicode[STIX]{x1D70F}_{\text{A,r}}\doteq a/v_{\text{A,r}}$
is the Alfvén crossing time of the CS,
![]() $\unicode[STIX]{x1D702}$
is the (collisional) resistivity and
$\unicode[STIX]{x1D702}$
is the (collisional) resistivity and
![]() $S_{a}\doteq av_{\text{A,r}}/\unicode[STIX]{x1D702}$
is the Lundquist number. Using an estimate for the growth rate
$S_{a}\doteq av_{\text{A,r}}/\unicode[STIX]{x1D702}$
is the Lundquist number. Using an estimate for the growth rate
![]() $\unicode[STIX]{x1D6FE}_{\text{t}}$
of the fastest-growing collisional tearing mode with wavenumber
$\unicode[STIX]{x1D6FE}_{\text{t}}$
of the fastest-growing collisional tearing mode with wavenumber
![]() $k_{\text{t}}$
oriented along the CS (Furth et al.
Reference Furth, Killeen and Rosenbluth1963; Coppi et al.
Reference Coppi, Galvăo, Pellat, Rosenbluth and Rutherford1976; Uzdensky & Loureiro Reference Uzdensky and Loureiro2016), the validity condition for collisionless tearing theory to hold becomes
$k_{\text{t}}$
oriented along the CS (Furth et al.
Reference Furth, Killeen and Rosenbluth1963; Coppi et al.
Reference Coppi, Galvăo, Pellat, Rosenbluth and Rutherford1976; Uzdensky & Loureiro Reference Uzdensky and Loureiro2016), the validity condition for collisionless tearing theory to hold becomes
This gives
![]() $a\lesssim 10^{-6}~\text{pc}$
for the ICM parameters listed in § 1, a satisfiable constraint given that
$a\lesssim 10^{-6}~\text{pc}$
for the ICM parameters listed in § 1, a satisfiable constraint given that
![]() $\unicode[STIX]{x1D70C}_{i}\sim 10^{-9}~\text{pc}$
and the outer scale of ICM magnetic-field fluctuations is observationally inferred to be
$\unicode[STIX]{x1D70C}_{i}\sim 10^{-9}~\text{pc}$
and the outer scale of ICM magnetic-field fluctuations is observationally inferred to be
![]() ${\sim}10~\text{kpc}$
(Enßlin & Vogt Reference Enßlin and Vogt2006; Guidetti et al.
Reference Guidetti, Murgia, Govoni, Parma, Gregorini, de Ruiter, Cameron and Fanti2008; Bonafede et al.
Reference Bonafede, Feretti, Murgia, Govoni, Giovannini, Dallacasa, Dolag and Taylor2010; Vacca et al.
Reference Vacca, Murgia, Govoni, Feretti, Giovannini, Perley and Taylor2012; Govoni et al.
Reference Govoni, Murgia, Vacca, Loi, Girardi, Gastaldello, Giovannini, Feretti, Paladino and Carretti2017), comparable to the collisional mean free path. At the accretion radius of Sgr A
${\sim}10~\text{kpc}$
(Enßlin & Vogt Reference Enßlin and Vogt2006; Guidetti et al.
Reference Guidetti, Murgia, Govoni, Parma, Gregorini, de Ruiter, Cameron and Fanti2008; Bonafede et al.
Reference Bonafede, Feretti, Murgia, Govoni, Giovannini, Dallacasa, Dolag and Taylor2010; Vacca et al.
Reference Vacca, Murgia, Govoni, Feretti, Giovannini, Perley and Taylor2012; Govoni et al.
Reference Govoni, Murgia, Vacca, Loi, Girardi, Gastaldello, Giovannini, Feretti, Paladino and Carretti2017), comparable to the collisional mean free path. At the accretion radius of Sgr A
![]() $^{\ast }$
, this constraint is
$^{\ast }$
, this constraint is
![]() $a\lesssim 10^{-10}~\text{pc}$
, which is
$a\lesssim 10^{-10}~\text{pc}$
, which is
![]() ${\sim}10^{2}$
larger than
${\sim}10^{2}$
larger than
![]() $\unicode[STIX]{x1D70C}_{i}$
and
$\unicode[STIX]{x1D70C}_{i}$
and
![]() ${\sim}10^{8}$
times smaller than the collisional mean free path. As long as (2.5) is satisfied (which becomes easier as
${\sim}10^{8}$
times smaller than the collisional mean free path. As long as (2.5) is satisfied (which becomes easier as
![]() $a$
shrinks),
$a$
shrinks),
![]() $\unicode[STIX]{x1D6FE}_{\text{t}}$
and
$\unicode[STIX]{x1D6FE}_{\text{t}}$
and
![]() $k_{\text{t}}$
are estimated as follows.
$k_{\text{t}}$
are estimated as follows.
In a
![]() $\unicode[STIX]{x1D6FD}\gtrsim 1$
plasma when the tearing-mode instability parameter
$\unicode[STIX]{x1D6FD}\gtrsim 1$
plasma when the tearing-mode instability parameter
![]() $\unicode[STIX]{x1D6E5}^{\prime }(k_{\text{t}})$
(Furth et al.
Reference Furth, Killeen and Rosenbluth1963) is small, satisfying
$\unicode[STIX]{x1D6E5}^{\prime }(k_{\text{t}})$
(Furth et al.
Reference Furth, Killeen and Rosenbluth1963) is small, satisfying
![]() $\unicode[STIX]{x1D6E5}^{\prime }\unicode[STIX]{x1D6FF}_{\text{in}}\sim (\unicode[STIX]{x1D6E5}^{\prime }d_{e})^{2}\ll 1$
(‘FKR-like’; Karimabadi et al. (Reference Karimabadi, Daughton and Quest2005)),
$\unicode[STIX]{x1D6E5}^{\prime }\unicode[STIX]{x1D6FF}_{\text{in}}\sim (\unicode[STIX]{x1D6E5}^{\prime }d_{e})^{2}\ll 1$
(‘FKR-like’; Karimabadi et al. (Reference Karimabadi, Daughton and Quest2005)),
where
![]() $d_{e}$
and
$d_{e}$
and
![]() $d_{i}\doteq \unicode[STIX]{x1D70C}_{i}/\unicode[STIX]{x1D6FD}_{i}^{1/2}=d_{e}(m_{i}/m_{e})^{1/2}$
are, respectively, the electron and ion skin depths (Fitzpatrick & Porcelli Reference Fitzpatrick and Porcelli2004, Reference Fitzpatrick and Porcelli2007). (Our CS formation model leaves
$d_{i}\doteq \unicode[STIX]{x1D70C}_{i}/\unicode[STIX]{x1D6FD}_{i}^{1/2}=d_{e}(m_{i}/m_{e})^{1/2}$
are, respectively, the electron and ion skin depths (Fitzpatrick & Porcelli Reference Fitzpatrick and Porcelli2004, Reference Fitzpatrick and Porcelli2007). (Our CS formation model leaves
![]() $d_{e},d_{i}$
constant.) This growth rate is approximately independent of
$d_{e},d_{i}$
constant.) This growth rate is approximately independent of
![]() $k_{\text{t}}$
in a Harris sheet, for which
$k_{\text{t}}$
in a Harris sheet, for which
![]() $\unicode[STIX]{x1D6E5}^{\prime }a=2(1/k_{\text{t}}a-k_{\text{t}}a)\sim (k_{\text{t}}a)^{-1}$
at
$\unicode[STIX]{x1D6E5}^{\prime }a=2(1/k_{\text{t}}a-k_{\text{t}}a)\sim (k_{\text{t}}a)^{-1}$
at
![]() $k_{\text{t}}a\ll 1$
. The large-
$k_{\text{t}}a\ll 1$
. The large-
![]() $\unicode[STIX]{x1D6E5}^{\prime }$
(‘Coppi-like’) growth rate satisfies
$\unicode[STIX]{x1D6E5}^{\prime }$
(‘Coppi-like’) growth rate satisfies
independent of
![]() $\unicode[STIX]{x1D6E5}^{\prime }$
(Fitzpatrick & Porcelli Reference Fitzpatrick and Porcelli2007). An estimate for
$\unicode[STIX]{x1D6E5}^{\prime }$
(Fitzpatrick & Porcelli Reference Fitzpatrick and Porcelli2007). An estimate for
![]() $\unicode[STIX]{x1D6FE}_{\text{t}}$
and
$\unicode[STIX]{x1D6FE}_{\text{t}}$
and
![]() $k_{\text{t}}$
of the fastest-growing Coppi-like mode in a Harris sheet can be obtained by balancing (2.6) and (2.7):
$k_{\text{t}}$
of the fastest-growing Coppi-like mode in a Harris sheet can be obtained by balancing (2.6) and (2.7):
In what follows, we assume that pressure anisotropy does not appreciably modify these growth rates. This is because saturated mirrors maintain
![]() $\unicode[STIX]{x1D6E5}_{p}\simeq 1/\unicode[STIX]{x1D6FD}_{\bot }\ll 1$
, and so the resulting viscous stress effectively enhances the magnetic tension responsible for driving the tearing by a factor of only
$\unicode[STIX]{x1D6E5}_{p}\simeq 1/\unicode[STIX]{x1D6FD}_{\bot }\ll 1$
, and so the resulting viscous stress effectively enhances the magnetic tension responsible for driving the tearing by a factor of only
![]() $\simeq 3/2$
. Other works that postulate an initial
$\simeq 3/2$
. Other works that postulate an initial
![]() $\unicode[STIX]{x1D6E5}_{p}$
(customarily taken to be uniform and thus non-zero even at
$\unicode[STIX]{x1D6E5}_{p}$
(customarily taken to be uniform and thus non-zero even at
![]() $x=0$
) do not consider its rapid regulation by the mirror instability prior to the onset of tearing, and the enhanced
$x=0$
) do not consider its rapid regulation by the mirror instability prior to the onset of tearing, and the enhanced
![]() $\unicode[STIX]{x1D6FE}_{\text{t}}$
often found in linear calculations when
$\unicode[STIX]{x1D6FE}_{\text{t}}$
often found in linear calculations when
![]() $\unicode[STIX]{x1D6E5}_{p}>0$
is largely because the assumption
$\unicode[STIX]{x1D6E5}_{p}>0$
is largely because the assumption
![]() $B_{\text{g}}=0$
permits axis-crossing particle orbits in the inner regions of the CS and allows threshold-less instabilities such as the Weibel instability (e.g. Chen & Palmadesso Reference Chen and Palmadesso1984).
$B_{\text{g}}=0$
permits axis-crossing particle orbits in the inner regions of the CS and allows threshold-less instabilities such as the Weibel instability (e.g. Chen & Palmadesso Reference Chen and Palmadesso1984).
3 Reconnection onset when
 $\unicode[STIX]{x1D6E5}_{p}=0$
$\unicode[STIX]{x1D6E5}_{p}=0$
Before determining how mirror-unstable pressure anisotropy affects a gradually forming CS, we recapitulate the theory of CS disruption by tearing modes (Pucci & Velli Reference Pucci and Velli2014; Tenerani et al.
Reference Tenerani, Velli, Rappazzo and Pucci2015; Loureiro & Uzdensky Reference Loureiro and Uzdensky2016; Uzdensky & Loureiro Reference Uzdensky and Loureiro2016), specialized to the case of collisionless tearing in a high-
![]() $\unicode[STIX]{x1D6FD}$
plasma. That is, we ignore the production of pressure anisotropy during CS formation and instead determine when
$\unicode[STIX]{x1D6FD}$
plasma. That is, we ignore the production of pressure anisotropy during CS formation and instead determine when
![]() $L/a$
has increased enough for tearing modes to prompt reconnection.
$L/a$
has increased enough for tearing modes to prompt reconnection.
As the CS’s aspect ratio
![]() $L/a$
increases in time, modes with progressively larger mode number
$L/a$
increases in time, modes with progressively larger mode number
![]() $N\doteq k_{\text{t}}(t)L(t)=\text{const}.$
become unstable and undergo linear evolution with
$N\doteq k_{\text{t}}(t)L(t)=\text{const}.$
become unstable and undergo linear evolution with
![]() $\unicode[STIX]{x1D6FE}_{\text{t}}(N,\!t)$
increasing (see figure 1). Uzdensky & Loureiro (Reference Uzdensky and Loureiro2016) argued that the first tearing mode
$\unicode[STIX]{x1D6FE}_{\text{t}}(N,\!t)$
increasing (see figure 1). Uzdensky & Loureiro (Reference Uzdensky and Loureiro2016) argued that the first tearing mode
![]() $N$
to reach the end of its linear stage at the critical time
$N$
to reach the end of its linear stage at the critical time
![]() $t_{\text{cr}}(N)$
(when
$t_{\text{cr}}(N)$
(when
![]() $\unicode[STIX]{x1D6FE}_{\text{t}}\unicode[STIX]{x1D70F}_{\text{cs}}\gtrsim 1$
, neglecting logarithmic corrections (Comisso et al.
Reference Comisso, Lingam, Huang and Bhattacharjee2017)) will also be the first to undergo X-point collapse (defined by when the island width
$\unicode[STIX]{x1D6FE}_{\text{t}}\unicode[STIX]{x1D70F}_{\text{cs}}\gtrsim 1$
, neglecting logarithmic corrections (Comisso et al.
Reference Comisso, Lingam, Huang and Bhattacharjee2017)) will also be the first to undergo X-point collapse (defined by when the island width
![]() $w\sim 1/\unicode[STIX]{x1D6E5}^{\prime }$
) and, soon thereafter, disrupt the CS (
$w\sim 1/\unicode[STIX]{x1D6E5}^{\prime }$
) and, soon thereafter, disrupt the CS (
![]() $w\sim a$
). We adopt this argument and estimate the CS disruption time
$w\sim a$
). We adopt this argument and estimate the CS disruption time
![]() $t_{\text{disrupt}}$
for a collisionless Harris sheet with
$t_{\text{disrupt}}$
for a collisionless Harris sheet with
![]() $L(t)a(t)=\text{const}$
. (The same procedure can be used to investigate alternative CS profiles and evolution.) Note that, for the Harris-sheet profile,
$L(t)a(t)=\text{const}$
. (The same procedure can be used to investigate alternative CS profiles and evolution.) Note that, for the Harris-sheet profile,
![]() $\unicode[STIX]{x1D6FE}_{\text{t}}^{\text{FKR}}\approx \unicode[STIX]{x1D6FE}_{\text{t}}^{\text{max}}$
for
$\unicode[STIX]{x1D6FE}_{\text{t}}^{\text{FKR}}\approx \unicode[STIX]{x1D6FE}_{\text{t}}^{\text{max}}$
for
![]() $k_{\text{t}}a\ll 1$
(see (2.6) and (2.8a
)), so the only difference between these modes are their wavenumbers and, thus, their
$k_{\text{t}}a\ll 1$
(see (2.6) and (2.8a
)), so the only difference between these modes are their wavenumbers and, thus, their
![]() $\unicode[STIX]{x1D6E5}^{\prime }\sim 1/k_{\text{t}}a^{2}$
.
$\unicode[STIX]{x1D6E5}^{\prime }\sim 1/k_{\text{t}}a^{2}$
.

Figure 1. Qualitative plot of tearing growth rate
![]() $\unicode[STIX]{x1D6FE}_{\text{t}}$
versus mode number
$\unicode[STIX]{x1D6FE}_{\text{t}}$
versus mode number
![]() $N$
(see (2.6) and (2.7)) shortly after mirror production at
$N$
(see (2.6) and (2.7)) shortly after mirror production at
![]() $k_{y,\text{m}}^{\text{max}}a>1$
. Arrows indicate evolution as the CS aspect ratio (
$k_{y,\text{m}}^{\text{max}}a>1$
. Arrows indicate evolution as the CS aspect ratio (
![]() $L/a$
) increases, with
$L/a$
) increases, with
![]() $\unicode[STIX]{x1D6FE}_{\text{t}}$
approaching
$\unicode[STIX]{x1D6FE}_{\text{t}}$
approaching
![]() $\unicode[STIX]{x1D70F}_{\text{cs}}^{-1}$
(blue dashed line),
$\unicode[STIX]{x1D70F}_{\text{cs}}^{-1}$
(blue dashed line),
![]() $k_{\text{t}}$
approaching the large-
$k_{\text{t}}$
approaching the large-
![]() $\unicode[STIX]{x1D6E5}^{\prime }$
regime (
$\unicode[STIX]{x1D6E5}^{\prime }$
regime (
![]() $k_{\text{t}}\lesssim k_{\text{t}}^{\text{max}}$
) and mirrors affecting an increasing number of tearing modes (those with
$k_{\text{t}}\lesssim k_{\text{t}}^{\text{max}}$
) and mirrors affecting an increasing number of tearing modes (those with
![]() $k_{\text{t}}\gtrsim k_{y,\text{m}}^{\text{max}}$
).
$k_{\text{t}}\gtrsim k_{y,\text{m}}^{\text{max}}$
).
Each unstable mode
![]() $N$
starts in the small-
$N$
starts in the small-
![]() $\unicode[STIX]{x1D6E5}^{\prime }$
(‘FKR-like’) regime (
$\unicode[STIX]{x1D6E5}^{\prime }$
(‘FKR-like’) regime (
![]() $N>N_{\text{max}}(t)$
), with
$N>N_{\text{max}}(t)$
), with
![]() $\unicode[STIX]{x1D6FE}_{\text{t}}$
roughly independent of
$\unicode[STIX]{x1D6FE}_{\text{t}}$
roughly independent of
![]() $k_{\text{t}}$
for
$k_{\text{t}}$
for
![]() $k_{\text{t}}a\ll 1$
. However, because
$k_{\text{t}}a\ll 1$
. However, because
![]() $N_{\text{max}}\propto (L/a)(d_{i}/a)\propto a^{-3}$
increases in time, these FKR-like modes approach the large-
$N_{\text{max}}\propto (L/a)(d_{i}/a)\propto a^{-3}$
increases in time, these FKR-like modes approach the large-
![]() $\unicode[STIX]{x1D6E5}^{\prime }$
(‘Coppi-like’) regime, making the transition at
$\unicode[STIX]{x1D6E5}^{\prime }$
(‘Coppi-like’) regime, making the transition at
![]() $t=t_{\text{tr}}(N)$
when
$t=t_{\text{tr}}(N)$
when
Larger
![]() $N$
corresponds to larger
$N$
corresponds to larger
![]() $t_{\text{tr}}(N)$
, and so the first mode to make this transition is
$t_{\text{tr}}(N)$
, and so the first mode to make this transition is
![]() $N=1$
; i.e. at
$N=1$
; i.e. at
![]() $t=t_{\text{tr}}(1)$
, the fastest Coppi-like mode (see (2.8b
)) just fits inside the CS. All modes satisfying
$t=t_{\text{tr}}(1)$
, the fastest Coppi-like mode (see (2.8b
)) just fits inside the CS. All modes satisfying
![]() $k_{\text{t}}^{\text{max}}a\lesssim k_{\text{t}}a\ll 1$
obtain growth rates
$k_{\text{t}}^{\text{max}}a\lesssim k_{\text{t}}a\ll 1$
obtain growth rates
![]() $\unicode[STIX]{x1D6FE}_{\text{t}}\unicode[STIX]{x1D70F}_{\text{cs}}\gtrsim 1$
at roughly the same time,
$\unicode[STIX]{x1D6FE}_{\text{t}}\unicode[STIX]{x1D70F}_{\text{cs}}\gtrsim 1$
at roughly the same time,
![]() $t=t_{\text{cr}}$
, when (using (2.8a
))
$t=t_{\text{cr}}$
, when (using (2.8a
))
where
![]() $M_{\text{A,0}}\doteq \unicode[STIX]{x1D70F}_{\text{A,r}}(t=0)/\unicode[STIX]{x1D70F}_{\text{cs}}$
is the initial Alfvénic Mach number of the CS formation. These modes have
$M_{\text{A,0}}\doteq \unicode[STIX]{x1D70F}_{\text{A,r}}(t=0)/\unicode[STIX]{x1D70F}_{\text{cs}}$
is the initial Alfvénic Mach number of the CS formation. These modes have
This is an important distinction from the collisional MHD case, in which larger
![]() $N>N_{\text{cr}}$
corresponds to larger
$N>N_{\text{cr}}$
corresponds to larger
![]() $t_{\text{cr}}(N)$
(since
$t_{\text{cr}}(N)$
(since
![]() $\unicode[STIX]{x1D6FE}_{\text{t}}^{\text{FKR}}\propto k_{\text{t}}^{-2/5}$
at
$\unicode[STIX]{x1D6FE}_{\text{t}}^{\text{FKR}}\propto k_{\text{t}}^{-2/5}$
at
![]() $k_{\text{t}}a\ll 1$
instead of
$k_{\text{t}}a\ll 1$
instead of
![]() $k_{\text{t}}^{0}$
).
$k_{\text{t}}^{0}$
).
Another important distinction from the MHD case lies in the nonlinear evolution, during which the MHD FKR modes behave differently than the MHD Coppi modes. While the latter are expected to rapidly evolve towards X-point collapse soon after
![]() $t=t_{\text{cr}}$
due to their large
$t=t_{\text{cr}}$
due to their large
![]() $\unicode[STIX]{x1D6E5}^{\prime }$
, the former undergo secular ‘Rutherford’ evolution that increases
$\unicode[STIX]{x1D6E5}^{\prime }$
, the former undergo secular ‘Rutherford’ evolution that increases
![]() $\unicode[STIX]{x1D6E5}^{\prime }(k_{N})w_{N}$
for a given mode
$\unicode[STIX]{x1D6E5}^{\prime }(k_{N})w_{N}$
for a given mode
![]() $N$
until
$N$
until
![]() $w_{N}\sim 1/\unicode[STIX]{x1D6E5}^{\prime }$
(Rutherford Reference Rutherford1973; Waelbroeck Reference Waelbroeck1989, Reference Waelbroeck1993; Loureiro et al.
Reference Loureiro, Cowley, Dorland, Haines and Schekochihin2005; Arcis, Loureiro & Militello Reference Arcis, Loureiro and Militello2009). However, in the collisionless case, the FKR-like modes reach
$w_{N}\sim 1/\unicode[STIX]{x1D6E5}^{\prime }$
(Rutherford Reference Rutherford1973; Waelbroeck Reference Waelbroeck1989, Reference Waelbroeck1993; Loureiro et al.
Reference Loureiro, Cowley, Dorland, Haines and Schekochihin2005; Arcis, Loureiro & Militello Reference Arcis, Loureiro and Militello2009). However, in the collisionless case, the FKR-like modes reach
![]() $\unicode[STIX]{x1D6FE}_{\text{t}}\unicode[STIX]{x1D70F}_{\text{cs}}\sim 1$
at the same time as the fastest Coppi-like mode. If the latter is accessible, then the fastest-growing mode
$\unicode[STIX]{x1D6FE}_{\text{t}}\unicode[STIX]{x1D70F}_{\text{cs}}\sim 1$
at the same time as the fastest Coppi-like mode. If the latter is accessible, then the fastest-growing mode
![]() $N_{\text{max}}$
already has
$N_{\text{max}}$
already has
![]() $\unicode[STIX]{x1D6E5}^{\prime }d_{e}\sim 1$
at
$\unicode[STIX]{x1D6E5}^{\prime }d_{e}\sim 1$
at
![]() $t_{\text{cr}}(N_{\text{max}})$
and so X-point collapse likely occurs soon after (3.2) is satisfied. The CS is then said to be ‘disrupted’ at
$t_{\text{cr}}(N_{\text{max}})$
and so X-point collapse likely occurs soon after (3.2) is satisfied. The CS is then said to be ‘disrupted’ at
![]() $t_{\text{disrupt}}\sim t_{\text{cr}}(N_{\text{max}})$
. For there to be no Coppi-like modes when (3.2) is satisfied (i.e.
$t_{\text{disrupt}}\sim t_{\text{cr}}(N_{\text{max}})$
. For there to be no Coppi-like modes when (3.2) is satisfied (i.e.
![]() $N_{\text{cr}}<1$
),
$N_{\text{cr}}<1$
),
![]() $M_{\text{A,0}}\lesssim (m_{e}/m_{i})^{1/5}(d_{i}/L_{0})$
, a rather stringent condition that is difficult to satisfy when
$M_{\text{A,0}}\lesssim (m_{e}/m_{i})^{1/5}(d_{i}/L_{0})$
, a rather stringent condition that is difficult to satisfy when
![]() $\unicode[STIX]{x1D6FD}_{0}\gg 1$
and
$\unicode[STIX]{x1D6FD}_{0}\gg 1$
and
![]() $\unicode[STIX]{x1D70C}_{i0}/L_{0}\ll 1$
.
$\unicode[STIX]{x1D70C}_{i0}/L_{0}\ll 1$
.
That being said, given the uncertainties in the nonlinear evolution of collisionless tearing modes in a high-
![]() $\unicode[STIX]{x1D6FD}$
, magnetized plasma – especially regarding the existence (or non-existence) of a secular ‘Rutherford’ phase and the production of pressure anisotropy during X-point collapse – we focus primarily on the critical time for reconnection onset (when
$\unicode[STIX]{x1D6FD}$
, magnetized plasma – especially regarding the existence (or non-existence) of a secular ‘Rutherford’ phase and the production of pressure anisotropy during X-point collapse – we focus primarily on the critical time for reconnection onset (when
![]() $\unicode[STIX]{x1D6FE}_{\text{t}}\unicode[STIX]{x1D70F}_{\text{cs}}\gtrsim 1$
) rather than the CS disruption time (when
$\unicode[STIX]{x1D6FE}_{\text{t}}\unicode[STIX]{x1D70F}_{\text{cs}}\gtrsim 1$
) rather than the CS disruption time (when
![]() $w\sim a$
).Footnote
5
$w\sim a$
).Footnote
5

Figure 2. Qualitative illustration of magnetic-field lines in an evolving, mirror-infested Harris CS with
![]() $\unicode[STIX]{x1D703}\ll 1$
.
$\unicode[STIX]{x1D703}\ll 1$
.
4 Reconnection onset when
 $\unicode[STIX]{x1D6E5}_{p}\neq 0$
$\unicode[STIX]{x1D6E5}_{p}\neq 0$
We now consider the effects of mirrors on an evolving CS subject to tearing modes. Because different portions of the CS have different
![]() $\unicode[STIX]{x1D70C}_{i}$
and
$\unicode[STIX]{x1D70C}_{i}$
and
![]() $\unicode[STIX]{x1D70F}_{\text{pa}}$
, there will be a range of mirror wavenumbers,
$\unicode[STIX]{x1D70F}_{\text{pa}}$
, there will be a range of mirror wavenumbers,
![]() $k_{y,\text{m}}(x)$
, along the CS (see figure 2).
$k_{y,\text{m}}(x)$
, along the CS (see figure 2).
The smallest
![]() $k_{y,\text{m}}$
will be located the nearest to
$k_{y,\text{m}}$
will be located the nearest to
![]() $x=0$
where mirrors can form, since these regions have the largest values of
$x=0$
where mirrors can form, since these regions have the largest values of
![]() $\unicode[STIX]{x1D70C}_{i}$
and
$\unicode[STIX]{x1D70C}_{i}$
and
![]() $\unicode[STIX]{x1D70F}_{\text{pa}}$
. We argue that, since tearing modes with wavenumbers
$\unicode[STIX]{x1D70F}_{\text{pa}}$
. We argue that, since tearing modes with wavenumbers
![]() $k_{\text{t}}$
much smaller than this
$k_{\text{t}}$
much smaller than this
![]() $k_{y,\text{m}}^{\text{min}}$
will see a rapidly
$k_{y,\text{m}}^{\text{min}}$
will see a rapidly
![]() $y$
-varying magnetic field that averages to its unperturbed value, these modes are likely unaffected by the mirrors (or at least less affected than other modes). The largest
$y$
-varying magnetic field that averages to its unperturbed value, these modes are likely unaffected by the mirrors (or at least less affected than other modes). The largest
![]() $k_{y,\text{m}}$
will be located near
$k_{y,\text{m}}$
will be located near
![]() $|x|\sim a$
, where
$|x|\sim a$
, where
![]() $\unicode[STIX]{x1D70C}_{i}$
and
$\unicode[STIX]{x1D70C}_{i}$
and
![]() $\unicode[STIX]{x1D70F}_{\text{pa}}$
are at their smallest values. All tearing modes with
$\unicode[STIX]{x1D70F}_{\text{pa}}$
are at their smallest values. All tearing modes with
![]() $k_{\text{t}}\gg k_{y\text{,m}}^{\text{max}}$
will see an approximately uniform-in-
$k_{\text{t}}\gg k_{y\text{,m}}^{\text{max}}$
will see an approximately uniform-in-
![]() $y$
magnetic field, but will have their
$y$
magnetic field, but will have their
![]() $\unicode[STIX]{x1D6E5}^{\prime }(k_{\text{t}})$
enhanced by the mirrors’ effect on the
$\unicode[STIX]{x1D6E5}^{\prime }(k_{\text{t}})$
enhanced by the mirrors’ effect on the
![]() $x$
-variation of the CS profile. If the CS is able to stretch to the point where
$x$
-variation of the CS profile. If the CS is able to stretch to the point where
![]() $k_{y\text{,m}}^{\text{max}}\lesssim k_{\text{t}}^{\text{max}}$
before the onset of tearing, then all of the modes that are unaffected by the mirrors will have smaller growth rates and thus be unimportant for CS reconnection. The condition
$k_{y\text{,m}}^{\text{max}}\lesssim k_{\text{t}}^{\text{max}}$
before the onset of tearing, then all of the modes that are unaffected by the mirrors will have smaller growth rates and thus be unimportant for CS reconnection. The condition
![]() $k_{y\text{,m}}^{\text{max}}\lesssim k_{\text{t}}^{\text{max}}$
is thus a sufficient (but not necessary) condition for mirrors to matter.
$k_{y\text{,m}}^{\text{max}}\lesssim k_{\text{t}}^{\text{max}}$
is thus a sufficient (but not necessary) condition for mirrors to matter.
We now follow the evolution of
![]() $k_{y,\text{m}}^{\text{max}}$
as the CS evolves, and investigate the evolution of tearing modes with
$k_{y,\text{m}}^{\text{max}}$
as the CS evolves, and investigate the evolution of tearing modes with
![]() $k_{\text{t}}\gg k_{y,\text{m}}^{\text{max}}$
. We treat two cases, depending upon the size of the guide field and thus the component of the mirrors’ wavevector along the CS at
$k_{\text{t}}\gg k_{y,\text{m}}^{\text{max}}$
. We treat two cases, depending upon the size of the guide field and thus the component of the mirrors’ wavevector along the CS at
![]() $|x|\sim a$
,
$|x|\sim a$
,
With
![]() $k_{\bot ,\text{m}}/k_{\Vert ,\text{m}}\sim \unicode[STIX]{x1D6EC}_{\text{m,max}}^{-1/2}$
for the fastest-growing mirror mode, we have
$k_{\bot ,\text{m}}/k_{\Vert ,\text{m}}\sim \unicode[STIX]{x1D6EC}_{\text{m,max}}^{-1/2}$
for the fastest-growing mirror mode, we have
![]() $k_{y,\text{m}}\sim k_{\Vert ,\text{m}}$
for
$k_{y,\text{m}}\sim k_{\Vert ,\text{m}}$
for
![]() $\unicode[STIX]{x1D703}\ll \unicode[STIX]{x1D6EC}_{\text{m,max}}^{1/2}$
and
$\unicode[STIX]{x1D703}\ll \unicode[STIX]{x1D6EC}_{\text{m,max}}^{1/2}$
and
![]() $k_{y,\text{m}}\sim \unicode[STIX]{x1D703}k_{\bot ,\text{m}}$
for
$k_{y,\text{m}}\sim \unicode[STIX]{x1D703}k_{\bot ,\text{m}}$
for
![]() $\unicode[STIX]{x1D6EC}_{\text{m,max}}^{1/2}\ll \unicode[STIX]{x1D703}\lesssim 1$
. (In both cases,
$\unicode[STIX]{x1D6EC}_{\text{m,max}}^{1/2}\ll \unicode[STIX]{x1D703}\lesssim 1$
. (In both cases,
![]() $\unicode[STIX]{x1D6EC}_{\text{m,max}}\sim (d_{i}/a_{0})^{1/2}M_{\text{A,0}}^{1/2}$
.)
$\unicode[STIX]{x1D6EC}_{\text{m,max}}\sim (d_{i}/a_{0})^{1/2}M_{\text{A,0}}^{1/2}$
.)
4.1 When mirrors affect tearing if
 $\unicode[STIX]{x1D703}\ll \unicode[STIX]{x1D6EC}_{\text{m,max}}^{1/2}$
$\unicode[STIX]{x1D703}\ll \unicode[STIX]{x1D6EC}_{\text{m,max}}^{1/2}$
At
![]() $x\sim a$
, the local reconnecting field is near its asymptotic value and
$x\sim a$
, the local reconnecting field is near its asymptotic value and
![]() $\unicode[STIX]{x1D70F}_{\text{pa}}\sim \unicode[STIX]{x1D70F}_{\text{cs}}$
. Starting at time
$\unicode[STIX]{x1D70F}_{\text{pa}}\sim \unicode[STIX]{x1D70F}_{\text{cs}}$
. Starting at time
![]() $t_{\text{m}}\sim \unicode[STIX]{x1D70F}_{\text{cs}}/\unicode[STIX]{x1D6FD}_{0}\ll \unicode[STIX]{x1D70F}_{\text{cs}}$
, unstable mirror modes grow rapidly at this location (
$t_{\text{m}}\sim \unicode[STIX]{x1D70F}_{\text{cs}}/\unicode[STIX]{x1D6FD}_{0}\ll \unicode[STIX]{x1D70F}_{\text{cs}}$
, unstable mirror modes grow rapidly at this location (
![]() $a$
and
$a$
and
![]() $\unicode[STIX]{x1D70F}_{\text{A,r}}$
hardly change from their initial values in a time
$\unicode[STIX]{x1D70F}_{\text{A,r}}$
hardly change from their initial values in a time
![]() $t_{\text{m}}$
.) Unless tearing modes disrupt the CS within
$t_{\text{m}}$
.) Unless tearing modes disrupt the CS within
![]() $t_{\text{disrupt}}\lesssim \unicode[STIX]{x1D70F}_{\text{cs}}$
– which is extremely unlikely, requiring (3.2) to be satisfied within
$t_{\text{disrupt}}\lesssim \unicode[STIX]{x1D70F}_{\text{cs}}$
– which is extremely unlikely, requiring (3.2) to be satisfied within
![]() $\unicode[STIX]{x1D70F}_{\text{cs}}$
– these mirrors will saturate with
$\unicode[STIX]{x1D70F}_{\text{cs}}$
– these mirrors will saturate with
![]() $\unicode[STIX]{x1D6FF}B\sim B_{\text{r}}$
and
$\unicode[STIX]{x1D6FF}B\sim B_{\text{r}}$
and
where we have accounted for the Lagrangian stretching of the perturbations during CS formation.
To determine the effect of these mirrors on tearing, it is useful (as argued above) to first establish when
![]() $k_{y,\text{m}}^{\text{max}}(t)$
enters the large-
$k_{y,\text{m}}^{\text{max}}(t)$
enters the large-
![]() $\unicode[STIX]{x1D6E5}^{\prime }$
regime in which
$\unicode[STIX]{x1D6E5}^{\prime }$
regime in which
![]() $\unicode[STIX]{x1D6FE}_{\text{t}}\propto k$
(the leftmost portion of figure 1), i.e. when the mirrors influence the fastest-growing tearing modes. Combining (2.8b
) and (4.2), we find that
$\unicode[STIX]{x1D6FE}_{\text{t}}\propto k$
(the leftmost portion of figure 1), i.e. when the mirrors influence the fastest-growing tearing modes. Combining (2.8b
) and (4.2), we find that
![]() $a(t)$
must satisfy
$a(t)$
must satisfy
for
![]() $k_{y,\text{m}}^{\text{max}}(t)\lesssim k_{\text{t}}^{\text{max}}(t)$
. Equation (4.3) happens before the sheet would be disrupted in the absence of mirrors (see (3.2)) if
$k_{y,\text{m}}^{\text{max}}(t)\lesssim k_{\text{t}}^{\text{max}}(t)$
. Equation (4.3) happens before the sheet would be disrupted in the absence of mirrors (see (3.2)) if
which is easily satisfied under the conditions of interest. Thus, there will be a time at which all tearing modes with
![]() $k_{\text{t}}\gtrsim k_{\text{t}}^{\text{max}}$
are affected by mirrors. How the tearing progresses after (4.3) is satisfied will be discussed once the corresponding conditions for the other
$k_{\text{t}}\gtrsim k_{\text{t}}^{\text{max}}$
are affected by mirrors. How the tearing progresses after (4.3) is satisfied will be discussed once the corresponding conditions for the other
![]() $\unicode[STIX]{x1D703}$
-regime are derived.
$\unicode[STIX]{x1D703}$
-regime are derived.
4.2 When mirrors affect tearing if
 $\unicode[STIX]{x1D6EC}_{\text{m,max}}^{1/2}\ll \unicode[STIX]{x1D703}\lesssim 1$
$\unicode[STIX]{x1D6EC}_{\text{m,max}}^{1/2}\ll \unicode[STIX]{x1D703}\lesssim 1$
As
![]() $B_{\text{g}}$
is increased, things will continue in much the same way as in § 4.1 except that the initial
$B_{\text{g}}$
is increased, things will continue in much the same way as in § 4.1 except that the initial
![]() $k_{y,\text{m}}^{\text{max}}\sim \unicode[STIX]{x1D703}k_{\bot ,\text{m}}$
. That is, equation (4.2) is replaced by
$k_{y,\text{m}}^{\text{max}}\sim \unicode[STIX]{x1D703}k_{\bot ,\text{m}}$
. That is, equation (4.2) is replaced by
This means that the condition on
![]() $a(t)$
that
$a(t)$
that
![]() $k_{y,\text{m}}^{\text{max}}(t)\lesssim k_{\text{t}}^{\text{max}}(t)$
(cf. (4.3)) becomes
$k_{y,\text{m}}^{\text{max}}(t)\lesssim k_{\text{t}}^{\text{max}}(t)$
(cf. (4.3)) becomes
If the initial state satisfies
then (4.6) occurs before (3.2), when the sheet would be disrupted without the mirrors.
4.3 Mirror-stimulated onset of reconnection
If either (4.4) or (4.7) is satisfied, then mirrors influence all tearing modes before they could otherwise disrupt the CS in the absence of mirrors. We now quantify that influence, focusing on those tearing modes with
![]() $k_{\text{t}}\gg k_{y,\text{m}}^{\text{max}}$
(see (4.2) and (4.5)). As argued previously, these modes see a magnetic field that is roughly uniform in
$k_{\text{t}}\gg k_{y,\text{m}}^{\text{max}}$
(see (4.2) and (4.5)). As argued previously, these modes see a magnetic field that is roughly uniform in
![]() $y$
but is rapidly varying in
$y$
but is rapidly varying in
![]() $x$
due to the mirrors, with an initial
$x$
due to the mirrors, with an initial
![]() $k_{x,\text{m}}\sim k_{\bot ,\text{m}}$
that is then compressed by the CS formation with
$k_{x,\text{m}}\sim k_{\bot ,\text{m}}$
that is then compressed by the CS formation with
![]() $k_{x,\text{m}}(t)a(t)\sim \text{const}$
. This rapid variation enhances
$k_{x,\text{m}}(t)a(t)\sim \text{const}$
. This rapid variation enhances
![]() $\unicode[STIX]{x1D6FE}_{\text{t}}(k_{\text{t}})$
for these modes due to the smaller effective sheet thickness (estimated below), which affects both
$\unicode[STIX]{x1D6FE}_{\text{t}}(k_{\text{t}})$
for these modes due to the smaller effective sheet thickness (estimated below), which affects both
![]() $\unicode[STIX]{x1D6E5}^{\prime }(k_{\text{t}})$
and the Alfvén-crossing time
$\unicode[STIX]{x1D6E5}^{\prime }(k_{\text{t}})$
and the Alfvén-crossing time
![]() $\unicode[STIX]{x1D70F}_{\text{A,r}}$
(see (2.6) and (2.7)).
$\unicode[STIX]{x1D70F}_{\text{A,r}}$
(see (2.6) and (2.7)).
4.3.1 Model for a mirror-infested CS
We argue that
![]() $\unicode[STIX]{x1D70F}_{\text{A,r}}$
changes by a small amount, since mirrors modify
$\unicode[STIX]{x1D70F}_{\text{A,r}}$
changes by a small amount, since mirrors modify
![]() $\text{d}B_{y}/\text{d}x|_{x=0}$
by only a factor of order unity. To determine how
$\text{d}B_{y}/\text{d}x|_{x=0}$
by only a factor of order unity. To determine how
![]() $\unicode[STIX]{x1D6E5}^{\prime }(k)$
is modified, we adopt the following simple model for the magnetic-field profile of a mirror-infested Harris CS:
$\unicode[STIX]{x1D6E5}^{\prime }(k)$
is modified, we adopt the following simple model for the magnetic-field profile of a mirror-infested Harris CS:
where
![]() $k_{\text{max}}\gg a^{-1}$
is a parameter characterizing the peak
$k_{\text{max}}\gg a^{-1}$
is a parameter characterizing the peak
![]() $k_{x,\text{m}}$
occurring at the edge of the CS. This is a Wentzel–Kramers–Brillouin (WKB) approximation describing saturated mirrors with amplitude
$k_{x,\text{m}}$
occurring at the edge of the CS. This is a Wentzel–Kramers–Brillouin (WKB) approximation describing saturated mirrors with amplitude
![]() $\unicode[STIX]{x1D700}\sim O(1)$
times the local reconnecting field and wavenumber in the
$\unicode[STIX]{x1D700}\sim O(1)$
times the local reconnecting field and wavenumber in the
![]() $x$
-direction given by
$x$
-direction given by
![]() $k_{x}(x)=2k_{\text{max}}\,\text{sech}(x/a)\tanh (x/a)$
. This model was chosen because
$k_{x}(x)=2k_{\text{max}}\,\text{sech}(x/a)\tanh (x/a)$
. This model was chosen because
![]() $k_{x}(x=0)=0$
,
$k_{x}(x=0)=0$
,
![]() $k_{x}(x\rightarrow \infty )\rightarrow 0$
, and
$k_{x}(x\rightarrow \infty )\rightarrow 0$
, and
![]() $k_{x}(x)$
is maximal near the edge of the CS, as anticipated. (What follows is not particularly sensitive to this choice of
$k_{x}(x)$
is maximal near the edge of the CS, as anticipated. (What follows is not particularly sensitive to this choice of
![]() $k_{x}(x)$
.)
$k_{x}(x)$
.)
The resulting
![]() $\unicode[STIX]{x1D6E5}^{\prime }(k_{\text{t}})$
is obtained by numerically integrating the outer differential equation for the flux function,
$\unicode[STIX]{x1D6E5}^{\prime }(k_{\text{t}})$
is obtained by numerically integrating the outer differential equation for the flux function,
![]() $\unicode[STIX]{x1D713}$
(Furth et al.
Reference Furth, Killeen and Rosenbluth1963):
$\unicode[STIX]{x1D713}$
(Furth et al.
Reference Furth, Killeen and Rosenbluth1963):
with
![]() $B_{y}(x)$
given by (4.8). Then
$B_{y}(x)$
given by (4.8). Then
![]() $\unicode[STIX]{x1D6E5}^{\prime }\doteq \text{d}\,\text{ln}\,\unicode[STIX]{x1D713}/\text{d}x|_{x=0}$
for the solution that obeys reasonable boundary conditions; an example result is shown in figure 3(a). (Its shape does not change significantly as
$\unicode[STIX]{x1D6E5}^{\prime }\doteq \text{d}\,\text{ln}\,\unicode[STIX]{x1D713}/\text{d}x|_{x=0}$
for the solution that obeys reasonable boundary conditions; an example result is shown in figure 3(a). (Its shape does not change significantly as
![]() $\unicode[STIX]{x1D700}$
and
$\unicode[STIX]{x1D700}$
and
![]() $k_{\text{max}}$
vary.) Generally,
$k_{\text{max}}$
vary.) Generally,
![]() $\unicode[STIX]{x1D6E5}^{\prime }>0$
for
$\unicode[STIX]{x1D6E5}^{\prime }>0$
for
![]() $k_{\text{t}}$
smaller than the inverse of the effective sheet thickness,
$k_{\text{t}}$
smaller than the inverse of the effective sheet thickness,
![]() $a_{\text{eff}}$
, which we identify with the location
$a_{\text{eff}}$
, which we identify with the location
![]() $x_{\text{m}}$
of the peak in
$x_{\text{m}}$
of the peak in
![]() $B_{y}(x)$
closest to
$B_{y}(x)$
closest to
![]() $x=0$
(i.e. the location of the innermost mirror). As
$x=0$
(i.e. the location of the innermost mirror). As
![]() $k_{\text{t}}$
decreases from this value,
$k_{\text{t}}$
decreases from this value,
![]() $\unicode[STIX]{x1D6E5}^{\prime }(k_{\text{t}})$
rises sharply to saturate at
$\unicode[STIX]{x1D6E5}^{\prime }(k_{\text{t}})$
rises sharply to saturate at
![]() $k_{\text{t}}=k_{\text{sat}}$
with value
$k_{\text{t}}=k_{\text{sat}}$
with value
![]() $\unicode[STIX]{x1D6E5}_{\text{sat}}^{\prime }\sim 1/a_{\text{eff}}\sim 1/x_{\text{m}}$
, at which it is approximately constant until it nears the Harris-sheet
$\unicode[STIX]{x1D6E5}_{\text{sat}}^{\prime }\sim 1/a_{\text{eff}}\sim 1/x_{\text{m}}$
, at which it is approximately constant until it nears the Harris-sheet
![]() $\unicode[STIX]{x1D6E5}^{\prime }(k_{\text{t}})\sim 1/k_{\text{t}}a^{2}$
, which it then follows.
$\unicode[STIX]{x1D6E5}^{\prime }(k_{\text{t}})\sim 1/k_{\text{t}}a^{2}$
, which it then follows.
The corresponding
![]() $\unicode[STIX]{x1D6FE}_{\text{t}}(k_{\text{t}})$
shown in figure 3(b) depends on whether or not
$\unicode[STIX]{x1D6FE}_{\text{t}}(k_{\text{t}})$
shown in figure 3(b) depends on whether or not
![]() $\unicode[STIX]{x1D6E5}_{\text{sat}}^{\prime }d_{e}\ll 1$
. However, the maximum growth rate always occurs at
$\unicode[STIX]{x1D6E5}_{\text{sat}}^{\prime }d_{e}\ll 1$
. However, the maximum growth rate always occurs at
![]() $k_{\text{sat}}\sim 1/x_{\text{m}}$
, because of the
$k_{\text{sat}}\sim 1/x_{\text{m}}$
, because of the
![]() $k_{\text{t}}$
-dependence of (2.6) and (2.7). Thus, to determine the new
$k_{\text{t}}$
-dependence of (2.6) and (2.7). Thus, to determine the new
![]() $t_{\text{cr}}$
, we must calculate
$t_{\text{cr}}$
, we must calculate
![]() $x_{\text{m}}$
. This yields two cases based on the size of
$x_{\text{m}}$
. This yields two cases based on the size of
![]() $\unicode[STIX]{x1D703}$
.
$\unicode[STIX]{x1D703}$
.

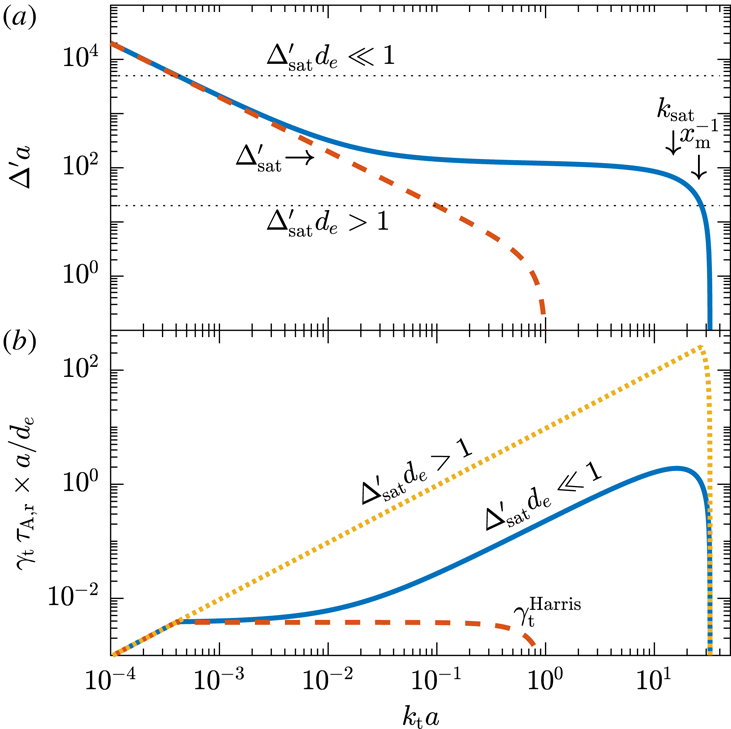
Figure 3. Values of (a)
![]() $\unicode[STIX]{x1D6E5}^{\prime }(k_{\text{t}})$
and (b)
$\unicode[STIX]{x1D6E5}^{\prime }(k_{\text{t}})$
and (b)
![]() $\unicode[STIX]{x1D6FE}_{\text{t}}(k_{\text{t}})$
for a Harris CS (red dashed line) and its mirror-infested counterpart (blue solid line), using
$\unicode[STIX]{x1D6FE}_{\text{t}}(k_{\text{t}})$
for a Harris CS (red dashed line) and its mirror-infested counterpart (blue solid line), using
![]() $k_{\text{max}}a=200\unicode[STIX]{x03C0}$
and
$k_{\text{max}}a=200\unicode[STIX]{x03C0}$
and
![]() $\unicode[STIX]{x1D700}=1/2$
in (4.8):
$\unicode[STIX]{x1D700}=1/2$
in (4.8):
![]() $\unicode[STIX]{x1D6E5}^{\prime }$
rises rapidly at
$\unicode[STIX]{x1D6E5}^{\prime }$
rises rapidly at
![]() $k_{\text{t}}x_{\text{m}}\lesssim 1$
and plateaus for
$k_{\text{t}}x_{\text{m}}\lesssim 1$
and plateaus for
![]() $k_{\text{sat}}\gtrsim k_{\text{t}}\gtrsim 1/(\unicode[STIX]{x1D6E5}_{\text{sat}}^{\prime }a^{2})$
. Mirror-stimulated tearing thus peaks at
$k_{\text{sat}}\gtrsim k_{\text{t}}\gtrsim 1/(\unicode[STIX]{x1D6E5}_{\text{sat}}^{\prime }a^{2})$
. Mirror-stimulated tearing thus peaks at
![]() $k_{\text{t}}\sim k_{\text{sat}}$
, regardless of whether
$k_{\text{t}}\sim k_{\text{sat}}$
, regardless of whether
![]() $\unicode[STIX]{x1D6E5}_{\text{sat}}^{\prime }d_{e}\ll 1$
(blue solid line) or
$\unicode[STIX]{x1D6E5}_{\text{sat}}^{\prime }d_{e}\ll 1$
(blue solid line) or
![]() $\unicode[STIX]{x1D6E5}_{\text{sat}}^{\prime }d_{e}\gtrsim 1$
(orange dotted line).
$\unicode[STIX]{x1D6E5}_{\text{sat}}^{\prime }d_{e}\gtrsim 1$
(orange dotted line).
4.3.2 Mirror-stimulated tearing for
 $\unicode[STIX]{x1D703}\ll x_{\text{m}}/a$
$\unicode[STIX]{x1D703}\ll x_{\text{m}}/a$
When the reconnecting field is the dominant field on the scale of the innermost mirrors, the total ion-Larmor frequency is
![]() $\unicode[STIX]{x1D6FA}_{i}\sim (x_{\text{m}}/a)\unicode[STIX]{x1D6FA}_{i,\text{r}}$
and
$\unicode[STIX]{x1D6FA}_{i}\sim (x_{\text{m}}/a)\unicode[STIX]{x1D6FA}_{i,\text{r}}$
and
![]() $\unicode[STIX]{x1D70F}_{\text{pa}}\sim \unicode[STIX]{x1D70F}_{\text{cs}}$
. The
$\unicode[STIX]{x1D70F}_{\text{pa}}\sim \unicode[STIX]{x1D70F}_{\text{cs}}$
. The
![]() $x$
-wavenumber of the mirrors at that location is then
$x$
-wavenumber of the mirrors at that location is then
where we have accounted for the Lagrangian compression due to CS formation. The innermost mirror is located at
![]() $x_{\text{m}}\sim k_{x,\text{m}}^{-1}$
, an
$x_{\text{m}}\sim k_{x,\text{m}}^{-1}$
, an
![]() $x$
-wavelength away from the centre. Substituting this into (4.10) yields
$x$
-wavelength away from the centre. Substituting this into (4.10) yields
For this estimate to be self-consistent, we require
![]() $\unicode[STIX]{x1D703}\ll x_{\text{m}}/a$
or, using (4.11),
$\unicode[STIX]{x1D703}\ll x_{\text{m}}/a$
or, using (4.11),
Provided this is satisfied, the fastest-growing tearing mode, having
![]() $\unicode[STIX]{x1D6FE}_{\text{t}}(k_{\text{sat}})$
, is either FKR-like, if
$\unicode[STIX]{x1D6FE}_{\text{t}}(k_{\text{sat}})$
, is either FKR-like, if
![]() $d_{e}/x_{\text{m}}\ll 1$
, or Coppi-like, if
$d_{e}/x_{\text{m}}\ll 1$
, or Coppi-like, if
![]() $d_{e}/x_{\text{m}}\gtrsim 1$
.
$d_{e}/x_{\text{m}}\gtrsim 1$
.
In the former case, the maximum tearing growth rate is (using (2.6) with
![]() $k_{\text{t}}\sim 1/x_{\text{m}}$
and
$k_{\text{t}}\sim 1/x_{\text{m}}$
and
![]() $\unicode[STIX]{x1D6E5}^{\prime }\sim 1/x_{\text{m}}$
)
$\unicode[STIX]{x1D6E5}^{\prime }\sim 1/x_{\text{m}}$
)
The critical time for onset,
![]() $t_{\text{cr}}^{\text{FKR}}$
, occurs when
$t_{\text{cr}}^{\text{FKR}}$
, occurs when
![]() $\unicode[STIX]{x1D6FE}_{\text{t,m}}^{\text{FKR}}\unicode[STIX]{x1D70F}_{\text{cs}}\sim 1$
, or
$\unicode[STIX]{x1D6FE}_{\text{t,m}}^{\text{FKR}}\unicode[STIX]{x1D70F}_{\text{cs}}\sim 1$
, or
In the latter (Coppi-like) case, which happens when
the maximum growth rate is
and so the critical time
![]() $t_{\text{cr}}^{\text{Coppi}}$
occurs when
$t_{\text{cr}}^{\text{Coppi}}$
occurs when
![]() $\unicode[STIX]{x1D6FE}_{\text{t,m}}^{\text{Coppi}}\unicode[STIX]{x1D70F}_{\text{cs}}\sim 1$
, or
$\unicode[STIX]{x1D6FE}_{\text{t,m}}^{\text{Coppi}}\unicode[STIX]{x1D70F}_{\text{cs}}\sim 1$
, or
If the smallest parameter in the problem is
![]() $d_{i}/a_{0}$
, so that (4.14) occurs before (4.15) (i.e.
$d_{i}/a_{0}$
, so that (4.14) occurs before (4.15) (i.e.
![]() $t_{\text{cr}}^{\text{FKR}}<t_{\text{tr}}$
), then the CS will go unstable to mirror-stimulated FKR-like modes before the fastest-growing mode enters the large-
$t_{\text{cr}}^{\text{FKR}}<t_{\text{tr}}$
), then the CS will go unstable to mirror-stimulated FKR-like modes before the fastest-growing mode enters the large-
![]() $\unicode[STIX]{x1D6E5}^{\prime }$
regime. In this case, the critical CS thickness,
$\unicode[STIX]{x1D6E5}^{\prime }$
regime. In this case, the critical CS thickness,
![]() $a_{\text{cr}}$
, is given by (4.14). Comparing this to the expression for
$a_{\text{cr}}$
, is given by (4.14). Comparing this to the expression for
![]() $a_{\text{cr}}$
when pressure anisotropy is not considered, equation (3.2), we see that mirrors increase
$a_{\text{cr}}$
when pressure anisotropy is not considered, equation (3.2), we see that mirrors increase
![]() $a_{\text{cr}}$
by a factor of
$a_{\text{cr}}$
by a factor of
![]() ${\sim}(d_{i}/a_{0})^{-2/7}\unicode[STIX]{x1D6FD}_{\text{r}}^{-4/7}M_{\text{A,0}}^{2/21}$
. If, instead,
${\sim}(d_{i}/a_{0})^{-2/7}\unicode[STIX]{x1D6FD}_{\text{r}}^{-4/7}M_{\text{A,0}}^{2/21}$
. If, instead,
![]() $t_{\text{cr}}^{\text{FKR}}>t_{\text{tr}}$
, then the fastest-growing mirror-stimulated tearing mode becomes Coppi-like before tearing onsets, and
$t_{\text{cr}}^{\text{FKR}}>t_{\text{tr}}$
, then the fastest-growing mirror-stimulated tearing mode becomes Coppi-like before tearing onsets, and
![]() $a_{\text{cr}}$
is effectively increased by a factor of
$a_{\text{cr}}$
is effectively increased by a factor of
![]() ${\sim}(m_{e}/m_{i})^{-1/15}(d_{i}/a_{0})^{-8/21}\unicode[STIX]{x1D6FD}_{\text{r}}^{-1/7}M_{\text{A,0}}^{-2/21}$
.
${\sim}(m_{e}/m_{i})^{-1/15}(d_{i}/a_{0})^{-8/21}\unicode[STIX]{x1D6FD}_{\text{r}}^{-1/7}M_{\text{A,0}}^{-2/21}$
.
4.3.3 Mirror-stimulated tearing for
 $\unicode[STIX]{x1D703}\sim x_{\text{m}}/a$
$\unicode[STIX]{x1D703}\sim x_{\text{m}}/a$
If (4.12) is not satisfied, then the innermost mirror does not reach the centre of the CS (i.e.
![]() $k_{x,\text{m}}x_{\text{m}}\gg 1$
). Instead, the mirrors closest to the centre with growth rate comparable to
$k_{x,\text{m}}x_{\text{m}}\gg 1$
). Instead, the mirrors closest to the centre with growth rate comparable to
![]() $\unicode[STIX]{x1D70F}_{\text{cs}}^{-1}$
are most important, i.e. those located at
$\unicode[STIX]{x1D70F}_{\text{cs}}^{-1}$
are most important, i.e. those located at
![]() $x_{\text{m}}\sim \unicode[STIX]{x1D703}a$
(see (2.2)). Then the scaling laws in the previous section are modified; equations (4.13)–(4.17) become, respectively,
$x_{\text{m}}\sim \unicode[STIX]{x1D703}a$
(see (2.2)). Then the scaling laws in the previous section are modified; equations (4.13)–(4.17) become, respectively,
Comparing (4.19) and (4.20), we see that, if
![]() $d_{i}/(\unicode[STIX]{x1D703}a_{0})\lesssim (m_{e}/m_{i})^{-1}M_{\text{A,0}}^{-1}$
, tearing will onset before the fastest-growing mode can enter the large-
$d_{i}/(\unicode[STIX]{x1D703}a_{0})\lesssim (m_{e}/m_{i})^{-1}M_{\text{A,0}}^{-1}$
, tearing will onset before the fastest-growing mode can enter the large-
![]() $\unicode[STIX]{x1D6E5}^{\prime }$
regime (i.e.
$\unicode[STIX]{x1D6E5}^{\prime }$
regime (i.e.
![]() $t_{\text{cr}}^{\text{FKR}}<t_{\text{tr}}$
). In this case,
$t_{\text{cr}}^{\text{FKR}}<t_{\text{tr}}$
). In this case,
![]() $a_{\text{cr}}$
is given by (4.19), which is larger by a factor of
$a_{\text{cr}}$
is given by (4.19), which is larger by a factor of
![]() ${\sim}\unicode[STIX]{x1D703}^{-2/3}$
than
${\sim}\unicode[STIX]{x1D703}^{-2/3}$
than
![]() $a_{\text{cr}}$
derived without consideration of the mirrors, equation (3.2). Therefore, tearing will onset much sooner if
$a_{\text{cr}}$
derived without consideration of the mirrors, equation (3.2). Therefore, tearing will onset much sooner if
![]() $\unicode[STIX]{x1D703}\ll 1$
, whereas
$\unicode[STIX]{x1D703}\ll 1$
, whereas
![]() $t_{\text{cr}}$
is largely unaffected when
$t_{\text{cr}}$
is largely unaffected when
![]() $\unicode[STIX]{x1D703}\sim 1$
. If, instead,
$\unicode[STIX]{x1D703}\sim 1$
. If, instead,
![]() $t_{\text{cr}}^{\text{FKR}}>t_{\text{tr}}$
, the mirror-stimulated tearing is Coppi-like, and
$t_{\text{cr}}^{\text{FKR}}>t_{\text{tr}}$
, the mirror-stimulated tearing is Coppi-like, and
![]() $a_{\text{cr}}$
is given by (4.22). However, the condition (4.12) still must be satisfied, allowing only a narrow range of validity for
$a_{\text{cr}}$
is given by (4.22). However, the condition (4.12) still must be satisfied, allowing only a narrow range of validity for
![]() $\unicode[STIX]{x1D703}$
. Moreover, this range only exists if
$\unicode[STIX]{x1D703}$
. Moreover, this range only exists if
![]() $d_{i}/a_{0}\gg (m_{e}/m_{i})^{-7/4}\unicode[STIX]{x1D6FD}_{\text{r}}^{1/2}M_{\text{A,0}}^{-2}$
, a constraint not likely to be satisfied in the regime of interest. We therefore choose (4.19) as the relevant condition for the onset of mirror-stimulated tearing for
$d_{i}/a_{0}\gg (m_{e}/m_{i})^{-7/4}\unicode[STIX]{x1D6FD}_{\text{r}}^{1/2}M_{\text{A,0}}^{-2}$
, a constraint not likely to be satisfied in the regime of interest. We therefore choose (4.19) as the relevant condition for the onset of mirror-stimulated tearing for
![]() $\unicode[STIX]{x1D703}\sim x_{\text{m}}/a$
.
$\unicode[STIX]{x1D703}\sim x_{\text{m}}/a$
.
5 Discussion
While the specific quantitative model of CS evolution and mirror-stimulated tearing formulated herein is perhaps debatable, it nevertheless demonstrates an important, qualitative point: a gradually forming CS in a high-
![]() $\unicode[STIX]{x1D6FD}$
, collisionless plasma easily produces enough pressure anisotropy to trigger the mirror instability, and the effect of this instability on the magnetic-field-line topology, and thus the tearing modes that instigate CS disruption via reconnection, ought to be considered.Footnote
6
For reasonable parameters, our theory predicts that the onset of reconnection in an evolving CS, driven by mirror-stimulated tearing modes, likely occurs earlier and at smaller scales than it would have without the mirrors, thereby placing a tighter upper limit on the aspect ratio of any forming CS (e.g. compare (4.14), (4.17) and (4.19) for the critical CS thickness at which mirror-stimulated tearing onsets to their
$\unicode[STIX]{x1D6FD}$
, collisionless plasma easily produces enough pressure anisotropy to trigger the mirror instability, and the effect of this instability on the magnetic-field-line topology, and thus the tearing modes that instigate CS disruption via reconnection, ought to be considered.Footnote
6
For reasonable parameters, our theory predicts that the onset of reconnection in an evolving CS, driven by mirror-stimulated tearing modes, likely occurs earlier and at smaller scales than it would have without the mirrors, thereby placing a tighter upper limit on the aspect ratio of any forming CS (e.g. compare (4.14), (4.17) and (4.19) for the critical CS thickness at which mirror-stimulated tearing onsets to their
![]() $\unicode[STIX]{x1D6E5}_{p}=0$
counterpart, equation (3.2)). Whether or not these mirror-stimulated tearing modes ultimately grow to amplitudes
$\unicode[STIX]{x1D6E5}_{p}=0$
counterpart, equation (3.2)). Whether or not these mirror-stimulated tearing modes ultimately grow to amplitudes
![]() $w\sim a_{\text{eff}}$
, and perhaps beyond to
$w\sim a_{\text{eff}}$
, and perhaps beyond to
![]() ${\sim}a$
via island coalescence, to disrupt the CS awaits further work.
${\sim}a$
via island coalescence, to disrupt the CS awaits further work.
An immediate practical implication of this result is that numerical simulations of collisionless reconnection in high-
![]() $\unicode[STIX]{x1D6FD}$
plasmas should not initialize with a Maxwellian plasma embedded in an equilibrium CS. Instead, the CS should be allowed to evolve, and the particle distribution function self-consistently with it. A natural testing ground for this theory is the kinetic magnetorotational instability (MRI) (Quataert, Dorland & Hammett Reference Quataert, Dorland and Hammett2002; Heinemann & Quataert Reference Heinemann and Quataert2014), thought to be the main driver of turbulence and enhanced transport in collisionless accretion flows, such as that onto the supermassive black hole at the Galactic centre (Sharma et al.
Reference Sharma, Hammett, Quataert and Stone2006). Historically, the linear MRI, at least in its MHD guise (Balbus & Hawley Reference Balbus and Hawley1991), was quickly shown to be a nonlinear ‘channel’ solution in a differentially rotating disk (Goodman & Xu Reference Goodman and Xu1994), and various studies followed that employed Kelvin–Helmholtz and tearing ‘parasitic’ modes to disrupt the otherwise resilient channels. In some theories, this disruption is credited for setting the steady-state level of magnetorotational turbulence as a function of the dissipative properties of the underlying magnetized fluid (e.g. Pessah & Goodman Reference Pessah and Goodman2009). Given that the kinetic MRI both linearly and nonlinearly drives pressure anisotropy (Squire, Quataert & Kunz Reference Squire, Quataert and Kunz2017), it is worthwhile to contemplate a similar sequence of events, in which the kinetic MRI breaks down due to tearing modes stimulated by ion-Larmor-scale mirrors. Kinetic simulations of the MRI (e.g. Riquelme et al.
Reference Riquelme, Quataert, Sharma and Spitkovsky2012; Hoshino Reference Hoshino2013, Reference Hoshino2015; Kunz, Stone & Quataert Reference Kunz, Stone and Quataert2016; Inchingolo et al.
Reference Inchingolo, Grismayer, Loureiro, Fonseca and Silva2018) may already be capable of testing this idea.
$\unicode[STIX]{x1D6FD}$
plasmas should not initialize with a Maxwellian plasma embedded in an equilibrium CS. Instead, the CS should be allowed to evolve, and the particle distribution function self-consistently with it. A natural testing ground for this theory is the kinetic magnetorotational instability (MRI) (Quataert, Dorland & Hammett Reference Quataert, Dorland and Hammett2002; Heinemann & Quataert Reference Heinemann and Quataert2014), thought to be the main driver of turbulence and enhanced transport in collisionless accretion flows, such as that onto the supermassive black hole at the Galactic centre (Sharma et al.
Reference Sharma, Hammett, Quataert and Stone2006). Historically, the linear MRI, at least in its MHD guise (Balbus & Hawley Reference Balbus and Hawley1991), was quickly shown to be a nonlinear ‘channel’ solution in a differentially rotating disk (Goodman & Xu Reference Goodman and Xu1994), and various studies followed that employed Kelvin–Helmholtz and tearing ‘parasitic’ modes to disrupt the otherwise resilient channels. In some theories, this disruption is credited for setting the steady-state level of magnetorotational turbulence as a function of the dissipative properties of the underlying magnetized fluid (e.g. Pessah & Goodman Reference Pessah and Goodman2009). Given that the kinetic MRI both linearly and nonlinearly drives pressure anisotropy (Squire, Quataert & Kunz Reference Squire, Quataert and Kunz2017), it is worthwhile to contemplate a similar sequence of events, in which the kinetic MRI breaks down due to tearing modes stimulated by ion-Larmor-scale mirrors. Kinetic simulations of the MRI (e.g. Riquelme et al.
Reference Riquelme, Quataert, Sharma and Spitkovsky2012; Hoshino Reference Hoshino2013, Reference Hoshino2015; Kunz, Stone & Quataert Reference Kunz, Stone and Quataert2016; Inchingolo et al.
Reference Inchingolo, Grismayer, Loureiro, Fonseca and Silva2018) may already be capable of testing this idea.
Acknowledgements
Support for A.A. and M.W.K. was provided by U.S. DOE contract DE-AC02-09CH11466. This work benefited greatly from conversations with N. Loureiro, A. Schekochihin and D. Uzdensky, and from comments by the anonymous referees.