Hostname: page-component-848d4c4894-xfwgj Total loading time: 0 Render date: 2024-06-28T23:07:26.946Z Has data issue: false hasContentIssue false
  • English
  • Français

On quasisymmetric plasma equilibria sustained by small force

Published online by Cambridge University Press:  11 February 2021

Peter Constantin ,
Theodore D. Drivas  and
Daniel Ginsberg Open the ORCID record for Daniel Ginsberg [Opens in a new window]
Peter Constantin
Affiliation:
Department of Mathematics, Princeton University, Princeton, NJ08544, USA
Theodore D. Drivas
Affiliation:
Department of Mathematics, Princeton University, Princeton, NJ08544, USA
Daniel Ginsberg*
Affiliation:
Program in Applied and Computational Mathematics, Princeton University, Princeton, NJ08544, USA
*
†Email address for correspondence: dg42@math.princeton.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

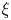We construct smooth, non-symmetric plasma equilibria which possess closed, nested flux surfaces and solve the magnetohydrostatic (steady three-dimensional incompressible Euler) equations with a small force. The solutions are also ‘nearly’ quasisymmetric. The primary idea is, given a desired quasisymmetry direction $\xi$, to change the smooth structure on space so that the vector field 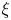$\xi$ is Killing for the new metric and construct $\xi$–symmetric solutions of the magnetohydrostatic equations on that background by solving a generalized Grad–Shafranov equation. If 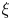$\xi$ is close to a symmetry of Euclidean space, then these are solutions on flat space up to a small forcing.

Keywords

fusion plasma
Type
Research Article
Information
Journal of Plasma Physics , Volume 87 , Issue 1 , February 2021 , 905870111
Copyright
Copyright © The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Arnold, V. I. & Khesin, B. A. 1999 Topological Methods in Hydrodynamics, vol. 125. Springer Science & Business Media.Google Scholar
Bernardin, M. P., Moses, R. W. & Tataronis, J. A. 1986 Isodynamical (omnigenous) equilibrium in symmetrically confined plasma configurations. Phys. Fluids 29 (8), 2605–2611.CrossRefGoogle Scholar
Burby, J. W., Kallinikos, N. & MacKay, R. S. 2020 Some mathematics for quasi-symmetry. J. Math. Phys. 61 (9), 093503.CrossRefGoogle Scholar
Burby, J. W., Kallinikos, N. & MacKay, R. S. 2020 Generalized Grad–Shafranov equation for non-axisymmetric MHD equilibria. Phys. Plasmas 27 (10), 102504.CrossRefGoogle Scholar
Bruno, O. P. & Laurence, P. 1996 Existence of three-dimensional toroidal MHD equilibria with nonconstant pressure. Commun. Pure Appl. Maths 49 (7), 717–764.3.0.CO;2-C>CrossRefGoogle Scholar
Constantin, P., Drivas, T. D. & Ginsberg, D. 2020 Flexibility and rigidity in steady fluid motion. arXiv:2007.09103.Google Scholar
Fecko, M. 2006 Differential Geometry and Lie Groups for Physicists. Cambridge University Press.CrossRefGoogle Scholar
Freidberg, J. 2014 Ideal MHD. Cambridge University Press.CrossRefGoogle Scholar
Garabedian, P. R. 2006 Three-dimensional equilibria in axially symmetric tokamaks. Proc. Natl Acad. Sci. USA 103 (51), 19232–19236.CrossRefGoogle ScholarPubMed
Garren, D. A. & Boozer, A. H. 1991 Existence of quasihelically symmetric stellarators. Phys. Fluids B 3 (10), 2822–2834.CrossRefGoogle Scholar
Grad, H. 1967 Toroidal containment of a plasma. Phys. Fluids 10 (1), 137–154.CrossRefGoogle Scholar
Grad, H. 1985 Theory and applications of the nonexistence of simple toroidal plasma equilibrium. Intl J. Fusion Energy 3 (2), 33–46.Google Scholar
Grad, H. & Rubin, H. 1958 Hydromagnetic equilibria and force-free fields. J. Nucl. Energy 7 (3–4), 284–285.Google Scholar
Hudson, S. R., Dewar, R. L., Dennis, G., Hole, M. J., McGann, M., Von Nessi, G. & Lazerson, S. 2012 Computation of multi-region relaxed magnetohydrodynamic equilibria. Phys. Plasmas 19 (11), 112502.CrossRefGoogle Scholar
Hudson, S. R., Dewar, R. L., Hole, M. J. & McGann, M. 2011 Non-axisymmetric, multi-region relaxed magnetohydrodynamic equilibrium solutions. Plasma Phys. Control. Fusion 54 (1), 014005.CrossRefGoogle Scholar
Jorge, R., Sengupta, W. & Landreman, M. 2019 Near-axis expansion of stellarator equilibrium at arbitrary order in the distance to the axis. arXiv:1911.02659.CrossRefGoogle Scholar
Kaiser, R. & Salat, A. 1997 New classes of three-dimensional ideal-MHD equilibria. J. Plasma Phys. 57, 425–448.CrossRefGoogle Scholar
Landreman, M. 2019 Quasisymmetry: a hidden symmetry of magnetic fields.Google Scholar
Lee, J. M. 2013 Smooth manifolds. In Introduction to Smooth Manifolds. Springer.CrossRefGoogle Scholar
Lichtenfelz, L., Misiolek, G. & Preston, S. C. 2019 Axisymmetric diffeomorphisms and ideal fluids on Riemannian 3-manifolds. arXiv:1911.10302.CrossRefGoogle Scholar
Lortz, D. 1970 Existence of toroidal magnetohydrostatic equilibrium without rotational transformation. Z. Angew. Math. Phys. 21, 196–211.CrossRefGoogle Scholar
Plunk, G. G. & Helander, P. 2018 Quasi-axisymmetric magnetic fields: weakly non-axisymmetric case in a vacuum. J. Plasma Phys. 84 (2).CrossRefGoogle Scholar
Rodriguez, E., Helander, P. & Bhattacharjee, A. 2020 Necessary and sufficient conditions for quasisymmetry. Phys. Plasmas 27 (6), 062501.CrossRefGoogle Scholar
Salat, A. & Kaiser, R. 1995 Three-dimensional closed field line magnetohydrodynamic equilibria without symmetries. Phys. Plasmas 2 (10), 3777–3781.CrossRefGoogle Scholar
Shafranov, V. D. 1966 Plasma equilibrium in a magnetic field. Rev. Plasma Phys. 2, 103.Google Scholar
Taylor, M. E. 1996 Partial Differential Equations III: Nonlinear Theory. Applied Mathematical Sciences, 117.Google Scholar
Weitzner, H. 2014 Ideal magnetohydrodynamic equilibrium in a non-symmetric topological torus. Phys. Plasmas 21 (2), 022515.CrossRefGoogle Scholar