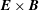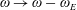1 Introduction
Plasmas of arbitrary neutrality, ranging from pure electron plasmas through to standard quasineutral ion–electron plasmas, can be confined in both stellarator (CNT) (Pedersen et al. Reference Pedersen, Boozer, Kremer, Lefrancois, Reiersen, Dahlgren and Pomphrey2004) and levitated dipole (RT-1, APEX) geometries (Pedersen et al. Reference Pedersen, Boozer, Dorland, Kremer and Schmitt2003; Yoshida et al. Reference Yoshida, Ogawa, Morikawa, Watanabe, Yano, Mizumaki, Tosaka, Ohtani, Hayakawa and Shiubi2006). Despite their laboratory and astrophysical relevance, relatively little has been done in terms of investigating the myriad of instabilities which can exist in such plasmas. In this work, we aim to examine certain classes of instabilities driven by two motivating examples.
1.1 Conventional plasmas
The Columbia Non-neutral Torus (CNT) is the first stellarator designed specifically to the study of pure electron and other non-neutral plasmas (Pedersen et al. Reference Pedersen, Boozer, Kremer, Lefrancois, Reiersen, Dahlgren and Pomphrey2004). Experiments undertaken at CNT have demonstrated that stable pure electron plasmas can enjoy good confinement. Stellarators are ideal candidates for the study of non-neutral plasmas as they are able to confine both signs of charge simultaneously and do not require internal currents for confinement. As such, stellarators are able to confine plasmas of arbitrary degree of neutrality (from pure electron to quasineutral). Stellarators present fundamental advantages for the study of non-neutral plasmas.
Despite enjoying good confinement properties, low-
![]() $\unicode[STIX]{x1D6FD}$
plasmas confined in toroidal magnetic geometries can develop low frequency instabilities which propagate at velocities of the order of the
$\unicode[STIX]{x1D6FD}$
plasmas confined in toroidal magnetic geometries can develop low frequency instabilities which propagate at velocities of the order of the
![]() $\boldsymbol{E}\times \boldsymbol{B}$
rotation velocity of the plasma. Indeed such low frequency instabilities have been observed in CNT.
$\boldsymbol{E}\times \boldsymbol{B}$
rotation velocity of the plasma. Indeed such low frequency instabilities have been observed in CNT.
One type of plasma oscillation which is of particular importance in quasineutral plasmas are drift waves. Of particular relevance to this work, such oscillations have also been observed for quasineutral plasmas in CNT. In their weakly non-neutral plasmas, multiple modes are excited and it becomes impossible to identify clear drift-wave signals (Sarasola & Pedersen Reference Sarasola and Pedersen2012). However, one might speculate that drift waves are amongst this medley of different modes, partly guided by the relative simplicity of the physical mechanisms involved. Drift waves are low frequency plasma oscillations driven by density and temperature gradients. Drift waves are well understood in quasineutral plasmas but have received little by way of theoretical attention in non-neutral plasmas.
Drift waves draw energy from the gradients of density and temperature in the plasma. The occurrence of these waves requires only that one species responds to the wave in an adiabatic fashion, thus Debye shielding the disturbance, due to either the difference in mass ratio, universal modes and ion-temperature-gradient (ITG) driven modes, or to finite Larmor radius (FLR) effects for electron-temperature-gradient (ETG) driven modes. The trigger for instability is the build up of electrostatic potential due to the different particle responses to an imposed perturbation. As discussed by Dubin (Reference Dubin2010), this in no way relies on different species having different signs of charge. The generality of these physical mechanisms lead us to believe that non-neutral plasmas can exhibit drift-wave phenomena.
Here, we use gyrokinetic theory to examine the stability of drift waves in plasmas of arbitrary neutrality in a shearless slab.
1.2 Electron–positron plasmas
The stability properties of non-neutral electron–positron plasmas will be of particular importance in the upcoming experiments to create and confine the first laboratory electron–positron plasma using a dipole field generated by a levitated magnetic coil (Saitoh et al. Reference Saitoh, Stanja, Stenson, Hergenhahn, Niemann, Pedersen, Stoneking, Piochacz and Hugenschmidt2015). Such a plasma ought to enjoy remarkable stability properties and a wealth of literature exists examining the stability of such systems. It has been shown by Helander (Reference Helander2014) that neutral pair plasmas possess unique gyrokinetic stability properties due to the mass symmetry between the particle species. For example, drift instabilities are completely absent in straight magnetic field geometry, e.g. in a slab, provided that the density and temperature profiles of the two species are identical (‘symmetric’ pair plasmas). The symmetry between the two species is broken if the temperature profiles of the electrons and positrons differ or there is an ion contamination. In these regimes, drift instabilities can be excited even in unsheared slab geometry (Mishchenko et al. Reference Mishchenko, Zocco, Helander and Könies2018b ). In a sheared slab, pure pair plasmas are prone to the current-driven reconnecting instabilities (Zocco Reference Zocco2017), but there are no drift waves. Note that asymmetry between the species is needed also in this case since the ambient electron flow velocity must differ from the positron one for the ambient current to be finite. In contrast to slab geometry, a dipole magnetic field has finite curvature. In this case, the symmetry between the species is broken by curvature drifts and the plasma is also driven unstable by temperature and density gradients (Helander Reference Helander2014), even without ion contamination and for identical temperature profiles of the two species. This result also persists in the electromagnetic regime (Helander & Connor Reference Helander and Connor2016). The nonlinear stability of dipole pair plasmas has also been addressed by Helander (Reference Helander2017). More recently, Mishchenko, Plunk & Helander (Reference Mishchenko, Plunk and Helander2018a ) performed a detailed study of the gyrokinetic stability of pure pair plasma in the dipole geometry, making use of both the Z-pinch and point-dipole limits. Again, it was found that such pair plasmas can be driven unstable by a combination of magnetic curvature, density and temperature gradients. Such instabilities in more complicated geometries such as the tokamak and the stellarator was also recently addressed using a gyrokinetic code by Kennedy et al. (Reference Kennedy, Mishchenko, Xanthopoulos and Helander2018).
One can effectively summarise previous results in one key statement: electron–positron plasmas are driven unstable by symmetry breaking between the two species. In this paper, we propose plasma non-neutrality as another way to break the species symmetry even in the simplest unsheared slab geometry.
It is once again pertinent to comment on how one might expect drift waves to be driven unstable in this case as there is certainly no species which now responds to the wave in an adiabatic fashion. That is, in electron–positron plasmas both species must be treated kinetically. However the underlying physical mechanism is simple, the unbalanced number of particles means that even though both species respond kinetically, there is no need for the drift contributions (which are in opposite directions due to the charge asymmetry) to locally cancel and therefore electrostatic potential can still accumulate.
Such plasmas are also physically realisable. During the upcoming PAX/APEX experiments it will be possible to operate the experiment in such a way that the plasma will be non-neutral. There is also relevance to the upcoming experiments during the accumulation process, singly charged electron plasmas and positron plasmas will be confined separately in modified Penning–Malmberg traps and hence we declare an interest in the stability of pure electron and positron plasmas as well as mixtures. The non-neutrality of these plasmas leads to the generation of large electric fields within the plasma which can impact the plasma stability. Here, we aim to present a simplified discussion on gyrokinetic modes in non-neutral plasmas.
Electron–positron plasmas ought to be ideal for modelling with gyrokinetics. The reason being that in the planned experiments the Debye length will exceed the gyroradius by several orders of magnitude. As the Debye length must be small compared to the system size, this means that the gyrokinetic ordering will be well satisfied for such plasmas.
1.3 Electron–antiproton plasmas
One can also use the tools described within this paper to tackle questions pertaining to the stability of multi-species non-neutral plasmas with only one sign of charge. An example of such a system is commonly encountered in the manufacture of cold antihydrogen for laser spectroscopy studies. In experiments such as ATHENA, low temperature antihydrogen atoms are formed from the interaction of several thousands of antiprotons with a dense positron plasma (Amoretti et al. Reference Amoretti, Carraro, Lagomarsino, Manuzio, Testera and Variola2002). Before being fed into the positron plasma, the antiprotons are cooled through the interaction with a cold dense electron plasma. This is an example of a non-neutral mutli-species plasma where all species have the same sign of charge.
Such non-neutral systems have been studied by Dubin (Reference Dubin2010) using a fluid model with an adiabatic light species, discussing both the simplified slab geometry considered here in tandem with a more experimentally relevant cylindrical geometry. It was found here that non-neutral plasmas consisting of two or more species can exhibit ion sound waves, drift waves and ion temperature-gradient waves, provided that certain conditions are met even in a more complex realistic geometry. Here, we will try to compliment this model using gyrokinetic theory to examine the stability of drift waves in such plasmas in a shearless slab.
1.4 Overview
In this paper we begin by extending the results of Mishchenko et al. (Reference Mishchenko, Zocco, Helander and Könies2018b ), performing a detailed study of the gyrokinetic stability of electron–positron–ion plasmas in slab geometries where we relax the condition of quasineutrality to derive and numerically solve a dispersion relation. We also investigate the particle fluxes due to the instabilities considered. The structure of this paper is as follows. In § 2 we introduce the analytical theory of non-neutral local gyrokinetic stability and derive the dispersion relation. We then give a brief discussion of some physical considerations and limits of our model. In § 3 we solve the dispersion relation for solutions of the sound wave type and give analytic estimates of the frequency. In § 4 we consider modes driven by density gradients. We solve the dispersion relation numerically for a range of different parameters and provide analytic estimates of the growth rate and real frequency. We elucidate the difference between non-neutral and quasineutral plasmas in this parameter regime, notably the existence of a second stability threshold for plasmas with large deviations from quasineutrality. In § 5 we discuss modes driven by the temperature gradient of the light species. Namely we investigate the stability of non-neutral plasmas with sufficiently large positron (electron) fractions to positron (electron)-temperature-gradient-driven instabilities. In § 6 we investigate the stability of non-neutral plasmas contaminated by an ion species. In § 7 we give our conclusions, highlighting the difference between these classes of instabilities in non-neutral plasmas compared to their quasineutral counterparts.
2 Gyrokinetic theory
Following Helander (Reference Helander2014), Helander & Connor (Reference Helander and Connor2016), Mishchenko et al. (Reference Mishchenko, Plunk and Helander2018a ) and Mishchenko et al. (Reference Mishchenko, Zocco, Helander and Könies2018b ), we will use gyrokinetic theory to analyse the stability of electron–positron–ion plasmas in this work, retaining the possibility of arbitrary degree of deviation from quasineutrality.
2.1 Dispersion relation
It is convenient to write the gyrokinetic distribution function in the form
Here,
![]() $f_{a0}$
is a Maxwellian,
$f_{a0}$
is a Maxwellian,
![]() $a$
is the species index with
$a$
is the species index with
![]() $a=e$
corresponding to electrons,
$a=e$
corresponding to electrons,
![]() $a=p$
to positrons and
$a=p$
to positrons and
![]() $a=i$
to the heavy ion species. We take care here to point out that in this work we will concern ourselves with both positively charged ions and negatively charged antiprotons, both of which will be denoted by the same subscript, the charge on species
$a=i$
to the heavy ion species. We take care here to point out that in this work we will concern ourselves with both positively charged ions and negatively charged antiprotons, both of which will be denoted by the same subscript, the charge on species
![]() $i$
will be assumed positive unless explicitly stated otherwise;
$i$
will be assumed positive unless explicitly stated otherwise;
![]() $\unicode[STIX]{x1D746}=\boldsymbol{b}\times \boldsymbol{v}/\unicode[STIX]{x1D6FA}_{a}$
is the species gyroradius and
$\unicode[STIX]{x1D746}=\boldsymbol{b}\times \boldsymbol{v}/\unicode[STIX]{x1D6FA}_{a}$
is the species gyroradius and
![]() $\unicode[STIX]{x1D6FA}_{a}$
the species cyclotron frequency. The remainder of the notation is standard.
$\unicode[STIX]{x1D6FA}_{a}$
the species cyclotron frequency. The remainder of the notation is standard.
The potential function for this system is given by
where
![]() $\unicode[STIX]{x1D719}_{0}$
is the background electrostatic potential due to the non-zero equilibrium electric field in the plasma,
$\unicode[STIX]{x1D719}_{0}$
is the background electrostatic potential due to the non-zero equilibrium electric field in the plasma,
![]() $\unicode[STIX]{x1D712}=\unicode[STIX]{x1D711}-v_{\Vert }A_{\Vert }$
is the usual gyrokinetic potential with
$\unicode[STIX]{x1D712}=\unicode[STIX]{x1D711}-v_{\Vert }A_{\Vert }$
is the usual gyrokinetic potential with
![]() $\unicode[STIX]{x1D711}$
the perturbed electrostatic potential and
$\unicode[STIX]{x1D711}$
the perturbed electrostatic potential and
![]() $A_{\Vert }$
the perturbed parallel magnetic potential.
$A_{\Vert }$
the perturbed parallel magnetic potential.
In this notation, the linearised gyrokinetic equation is
with
![]() $J_{0}$
the Bessel function,
$J_{0}$
the Bessel function,
![]() $k_{\bot }$
the perpendicular wave number,
$k_{\bot }$
the perpendicular wave number,
![]() $k_{\Vert }$
the parallel wavenumber. Other notation employed here is
$k_{\Vert }$
the parallel wavenumber. Other notation employed here is
with
Here we will choose the sign convention such that
![]() $\unicode[STIX]{x1D714}_{\star i}\leqslant 0,\unicode[STIX]{x1D714}_{\star p}\leqslant 0,$
and
$\unicode[STIX]{x1D714}_{\star i}\leqslant 0,\unicode[STIX]{x1D714}_{\star p}\leqslant 0,$
and
![]() $\unicode[STIX]{x1D714}_{\star e}\geqslant 0.$
In our slab geometry
$\unicode[STIX]{x1D714}_{\star e}\geqslant 0.$
In our slab geometry
![]() $x$
denotes the direction of any non-uniformity in the plasma profiles. For simplicity we will assume
$x$
denotes the direction of any non-uniformity in the plasma profiles. For simplicity we will assume
![]() $k_{x}=0$
and
$k_{x}=0$
and
![]() $k_{\bot }=k_{y}$
throughout the paper.
$k_{\bot }=k_{y}$
throughout the paper.
The influence of the background electric field is only felt through the term
a quantity which is locally constant. We will discuss the consequences of this local approximation at the end of the section.
In slab geometry
![]() $\unicode[STIX]{x1D714}_{da}=0$
and hence our equation may be trivially solved to give
$\unicode[STIX]{x1D714}_{da}=0$
and hence our equation may be trivially solved to give
This equation is supplemented by Poisson’s equation and the parallel Ampere’s law for the perturbation. These equations read
For the electromagnetic dispersion relation we will find it convenient to define the function
which may be evaluated to obtain
Here, the following notation has been used
We can substitute our equation for the gyrokinetic distribution function into each of the field equations and use the notation given above to obtain
This gives rise to the dispersion relation
 $$\begin{eqnarray}\displaystyle & & \displaystyle \left(1+k_{\bot }^{2}\unicode[STIX]{x1D706}_{D}^{2}+\mathop{\sum }_{a}\frac{\unicode[STIX]{x1D706}_{D}^{2}}{\unicode[STIX]{x1D706}_{Da}^{2}}W_{0a}\right)\left(1-2\mathop{\sum }_{a}\frac{\unicode[STIX]{x1D6FD}_{a}}{k_{\bot }^{2}\unicode[STIX]{x1D70C}_{a}^{2}}W_{2a}\right)\nonumber\\ \displaystyle & & \displaystyle \quad +\,2\mathop{\sum }_{a}\frac{\unicode[STIX]{x1D706}_{D}^{2}}{\unicode[STIX]{x1D706}_{Da}^{2}}W_{1a}v_{\text{th}a}\mathop{\sum }_{a}\frac{\unicode[STIX]{x1D6FD}_{a}}{k_{\bot }^{2}\unicode[STIX]{x1D70C}_{a}^{2}}\frac{W_{1a}}{v_{\text{th}a}}=0.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \left(1+k_{\bot }^{2}\unicode[STIX]{x1D706}_{D}^{2}+\mathop{\sum }_{a}\frac{\unicode[STIX]{x1D706}_{D}^{2}}{\unicode[STIX]{x1D706}_{Da}^{2}}W_{0a}\right)\left(1-2\mathop{\sum }_{a}\frac{\unicode[STIX]{x1D6FD}_{a}}{k_{\bot }^{2}\unicode[STIX]{x1D70C}_{a}^{2}}W_{2a}\right)\nonumber\\ \displaystyle & & \displaystyle \quad +\,2\mathop{\sum }_{a}\frac{\unicode[STIX]{x1D706}_{D}^{2}}{\unicode[STIX]{x1D706}_{Da}^{2}}W_{1a}v_{\text{th}a}\mathop{\sum }_{a}\frac{\unicode[STIX]{x1D6FD}_{a}}{k_{\bot }^{2}\unicode[STIX]{x1D70C}_{a}^{2}}\frac{W_{1a}}{v_{\text{th}a}}=0.\end{eqnarray}$$
Here
![]() $\unicode[STIX]{x1D6FD}_{a}=\unicode[STIX]{x1D707}_{0}n_{a}T_{a}/B^{2},$
the usual plasma beta. We will restrict our attention to the electrostatic limit, corresponding to
$\unicode[STIX]{x1D6FD}_{a}=\unicode[STIX]{x1D707}_{0}n_{a}T_{a}/B^{2},$
the usual plasma beta. We will restrict our attention to the electrostatic limit, corresponding to
![]() $\unicode[STIX]{x1D6FD}_{a}=0$
. This dispersion relation clearly reduces to the result of Mishchenko et al. (Reference Mishchenko, Zocco, Helander and Könies2018b
) in the limit of quasineutrality.
$\unicode[STIX]{x1D6FD}_{a}=0$
. This dispersion relation clearly reduces to the result of Mishchenko et al. (Reference Mishchenko, Zocco, Helander and Könies2018b
) in the limit of quasineutrality.
2.2 Quasilinear particle fluxes
Following Helander & Zocco (Reference Helander and Zocco2018), we define the cross-field particle flux of species
![]() $a$
to be given by
$a$
to be given by
where the angular brackets denote the flux surface average
which we remark has no effect in the straight field line limit considered here.
The non-neutral drift waves reported in this paper can also lead to cross-field particle diffusion. The particle flux due to drift-wave instabilities in standard electron–ion plasmas has been studied in the aforementioned paper by Helander & Zocco (Reference Helander and Zocco2018). Here, we are able to simplify certain aspects of the calculations by the restrictions placed on the geometry whilst introducing further complications by the non-neutrality.
We have already found that the equation for the perturbed part of the distribution function is given in the local limit by (2.3). Hence, the quasilinear particle flux of species
![]() $a$
is given by
$a$
is given by
which yields
Hence, one obtains
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6E4}_{a} & = & \displaystyle \frac{k_{y}}{B}\text{Im}\left\langle \frac{n_{a}e_{a}}{T_{a}}|\unicode[STIX]{x1D711}|^{2}\unicode[STIX]{x1D701}_{a}\left\{\left(1-\frac{\unicode[STIX]{x1D714}_{\star a}}{\unicode[STIX]{x1D714}-k_{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D719}_{0}^{\prime }}\right)Z_{0a}\unicode[STIX]{x1D6E4}_{0a}\right.\right.\nonumber\\ \displaystyle & & \displaystyle +\left.\left.\frac{\unicode[STIX]{x1D714}_{\star a}\unicode[STIX]{x1D702}_{a}}{\unicode[STIX]{x1D714}-k_{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D719}_{0}^{\prime }}\left[\frac{3}{2}Z_{0a}\unicode[STIX]{x1D6E4}_{0a}-Z_{0a}\unicode[STIX]{x1D6E4}_{\star a}-Z_{2,a}\unicode[STIX]{x1D6E4}_{0a}\right]\right\}\right\rangle .\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6E4}_{a} & = & \displaystyle \frac{k_{y}}{B}\text{Im}\left\langle \frac{n_{a}e_{a}}{T_{a}}|\unicode[STIX]{x1D711}|^{2}\unicode[STIX]{x1D701}_{a}\left\{\left(1-\frac{\unicode[STIX]{x1D714}_{\star a}}{\unicode[STIX]{x1D714}-k_{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D719}_{0}^{\prime }}\right)Z_{0a}\unicode[STIX]{x1D6E4}_{0a}\right.\right.\nonumber\\ \displaystyle & & \displaystyle +\left.\left.\frac{\unicode[STIX]{x1D714}_{\star a}\unicode[STIX]{x1D702}_{a}}{\unicode[STIX]{x1D714}-k_{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D719}_{0}^{\prime }}\left[\frac{3}{2}Z_{0a}\unicode[STIX]{x1D6E4}_{0a}-Z_{0a}\unicode[STIX]{x1D6E4}_{\star a}-Z_{2,a}\unicode[STIX]{x1D6E4}_{0a}\right]\right\}\right\rangle .\end{eqnarray}$$
We remark that it is of course very simple to extend the particle flux to the electromagnetic case, however the focus of this work is exclusively on
![]() $\unicode[STIX]{x1D6FD}_{a}=0$
plasmas and hence we shall not do so here.
$\unicode[STIX]{x1D6FD}_{a}=0$
plasmas and hence we shall not do so here.
It is well known that gyrokinetic transport is intrinsically ambipolar (Sugama et al. Reference Sugama, Okamoto, Horton and Wakatani1998) and it is easy to verify that this result also holds true in the non-neutral case. We calculate
where the final equality follows immediately from the electrostatic limit of the dispersion relation (2.17).
In this work, we will numerically calculate the quantity
Here,
![]() $|\unicode[STIX]{x1D711}|^{2}$
is a scaling factor associated with the saturation amplitude of the fluctuations, which does not need to be determined explicitly as we are primarily interested in the directions of the fluxes and any interesting behaviour exhibited. To this end, we remark that
$|\unicode[STIX]{x1D711}|^{2}$
is a scaling factor associated with the saturation amplitude of the fluctuations, which does not need to be determined explicitly as we are primarily interested in the directions of the fluxes and any interesting behaviour exhibited. To this end, we remark that
![]() $\unicode[STIX]{x1D6EC}_{a}$
is simply the particle current up to an unknown positive constant. We are able to calculate the quantity
$\unicode[STIX]{x1D6EC}_{a}$
is simply the particle current up to an unknown positive constant. We are able to calculate the quantity
![]() $\unicode[STIX]{x1D6EC}_{a}$
for the entire parameter range but note here that we only expect these to make some physical sense in the parameter ranges where the growth rate
$\unicode[STIX]{x1D6EC}_{a}$
for the entire parameter range but note here that we only expect these to make some physical sense in the parameter ranges where the growth rate
![]() $\unicode[STIX]{x1D6FE}>0$
i.e. where there is actually an instability present. It is worth remarking that usually one expects
$\unicode[STIX]{x1D6FE}>0$
i.e. where there is actually an instability present. It is worth remarking that usually one expects
![]() $|\unicode[STIX]{x1D711}|^{2}=0$
in the stable domain and hence the quasilinear fluxes
$|\unicode[STIX]{x1D711}|^{2}=0$
in the stable domain and hence the quasilinear fluxes
![]() $\unicode[STIX]{x1D6E4}_{a}=0$
in these domains. This rule of thumb is generally, but not always true and it may be the case that even in linearly stable domains, there is a particle transport driven by subcritical turbulence, i.e. the system is formally stable to small perturbations, but, given a large enough initial perturbation, it transitions to a turbulent state.
$\unicode[STIX]{x1D6E4}_{a}=0$
in these domains. This rule of thumb is generally, but not always true and it may be the case that even in linearly stable domains, there is a particle transport driven by subcritical turbulence, i.e. the system is formally stable to small perturbations, but, given a large enough initial perturbation, it transitions to a turbulent state.
2.3 Physical assumptions
In the local limit considered here, we have relegated the effect of the background electric field into a Doppler shift of the complex frequency
![]() $\unicode[STIX]{x1D714}\rightarrow \unicode[STIX]{x1D714}-k_{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D719}_{0}^{\prime }.$
This result has a simple physical interpretation, namely that in the frame rotating with the
$\unicode[STIX]{x1D714}\rightarrow \unicode[STIX]{x1D714}-k_{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D719}_{0}^{\prime }.$
This result has a simple physical interpretation, namely that in the frame rotating with the
![]() $\boldsymbol{E}\times \boldsymbol{B}$
velocity, the nascent electric field generated by the plasma is identically zero. Hence in this rotating frame we achieve precisely the result of Mishchenko et al. (Reference Mishchenko, Zocco, Helander and Könies2018b
). We note that in our model, the Doppler shift is arbitrary. The reason for this is that
$\boldsymbol{E}\times \boldsymbol{B}$
velocity, the nascent electric field generated by the plasma is identically zero. Hence in this rotating frame we achieve precisely the result of Mishchenko et al. (Reference Mishchenko, Zocco, Helander and Könies2018b
). We note that in our model, the Doppler shift is arbitrary. The reason for this is that
![]() $\unicode[STIX]{x1D719}_{0}$
does not appear explicitly in the zeroth-order Poisson equation for the length scales considered here:
$\unicode[STIX]{x1D719}_{0}$
does not appear explicitly in the zeroth-order Poisson equation for the length scales considered here:
![]() $\unicode[STIX]{x1D719}_{0}^{\prime \prime }/\unicode[STIX]{x1D719}_{0}\ll k_{\bot }^{2}$
. It may appear at first glance that this trivialises the dynamics of non-neutral plasmas insofar as one might expect the problem reduces exactly to Mishchenko et al. (Reference Mishchenko, Zocco, Helander and Könies2018b
). This is not the case.
$\unicode[STIX]{x1D719}_{0}^{\prime \prime }/\unicode[STIX]{x1D719}_{0}\ll k_{\bot }^{2}$
. It may appear at first glance that this trivialises the dynamics of non-neutral plasmas insofar as one might expect the problem reduces exactly to Mishchenko et al. (Reference Mishchenko, Zocco, Helander and Könies2018b
). This is not the case.
Despite the relatively straightforward, physically pleasing relationship between the dispersion relation for non-neutral and quasineutral plasmas in the local limit, there is more subtle difference at play. We recall that in Mishchenko et al. (Reference Mishchenko, Zocco, Helander and Könies2018b ) it was necessary for there to be symmetry breaking due to either the temperature profiles or ion contamination for instabilities to be excited. In a non-quasineutral plasma, there is another degree of freedom in the system as it permissible to violate the quasineutrality condition. A key stability parameter for three component non-neutral plasmas was the species fraction
where we note that a quasineutral plasma must satisfy the quasineutrality constraint
For a non-neutral plasma we have no such constraint and
![]() $\sum _{a}\unicode[STIX]{x1D708}_{a}$
may be arbitrary. Indeed, it is now possible to break the symmetry of the density profiles of even a simple pair plasma. This leads to a diversification in the types of gyrokinetic modes which can arise in such plasmas. Indeed, it is precisely this symmetry breaking (allowing us to take in pair plasma
$\sum _{a}\unicode[STIX]{x1D708}_{a}$
may be arbitrary. Indeed, it is now possible to break the symmetry of the density profiles of even a simple pair plasma. This leads to a diversification in the types of gyrokinetic modes which can arise in such plasmas. Indeed, it is precisely this symmetry breaking (allowing us to take in pair plasma
![]() $n_{e}\neq n_{p}$
for example) that gives rise to instabilities.
$n_{e}\neq n_{p}$
for example) that gives rise to instabilities.
Here we consider a local theory including ambient electric field, always present in a non-neutral plasma, but neglect the shear of this field. This is an important approximation which will be relaxed in future work. Indeed, it must be relaxed for the diocotron instability (Davidson Reference Davidson1974). It is well known that the global diocotron mode, an analogue of the shearing Kelvin–Helmholtz instability, plays a pivotal role in the dynamics of non-neutral plasmas. We plan to address this more complex question with a global gyrokinetic code in the future. In this paper we will consider only the local limit and concentrate solely on drift mode dynamics.
It is also pertinent to comment on the use of Ampere’s law in our derivation above. One ought to question whether there is a need to include the displacement current on the basis that we have included Debye shielding in Poisson’s equation. Here, Debye shielding is important due to having a sufficiently small plasma
![]() $\unicode[STIX]{x1D6FD}_{a}$
(which here means that
$\unicode[STIX]{x1D6FD}_{a}$
(which here means that
![]() $\unicode[STIX]{x1D6FD}_{a}\lesssim v_{\text{th}a}^{2}/c^{2}$
). This makes it necessary to include Debye shielding effects as
$\unicode[STIX]{x1D6FD}_{a}\lesssim v_{\text{th}a}^{2}/c^{2}$
). This makes it necessary to include Debye shielding effects as
![]() $\unicode[STIX]{x1D706}_{Da}^{2}/\unicode[STIX]{x1D70C}_{a}^{2}=(1/2\unicode[STIX]{x1D6FD}_{a})(v_{\text{th}a}^{2}/c^{2})$
and hence we expect the Debye length to be comparable to the electron Larmor radius. However, as pointed out by Barnes, Abiuso & Dorland (Reference Barnes, Abiuso and Dorland2018) we note that even when
$\unicode[STIX]{x1D706}_{Da}^{2}/\unicode[STIX]{x1D70C}_{a}^{2}=(1/2\unicode[STIX]{x1D6FD}_{a})(v_{\text{th}a}^{2}/c^{2})$
and hence we expect the Debye length to be comparable to the electron Larmor radius. However, as pointed out by Barnes, Abiuso & Dorland (Reference Barnes, Abiuso and Dorland2018) we note that even when
![]() $\unicode[STIX]{x1D706}_{Da}^{2}/\unicode[STIX]{x1D70C}_{a}^{2}\sim 1$
, the displacement current appearing in Ampere’s law is negligible in the gyrokinetic ordering compared to the plasma current. In this ordering the displacement current must only be retained when taking the divergence of Ampere’s law.
$\unicode[STIX]{x1D706}_{Da}^{2}/\unicode[STIX]{x1D70C}_{a}^{2}\sim 1$
, the displacement current appearing in Ampere’s law is negligible in the gyrokinetic ordering compared to the plasma current. In this ordering the displacement current must only be retained when taking the divergence of Ampere’s law.
3 Gyrokinetic stable modes
We first consider the case of a conventional electrostatic electron–hydrogen plasma, whilst dropping the usual assumption of quasineutrality. In this case, our dispersion relation (2.17) reduces to
In the absence of density and temperature gradients and assuming that both species have equal temperatures, i.e.
![]() $T_{i}=T_{e},$
we can further simplify the dispersion relation to obtain
$T_{i}=T_{e},$
we can further simplify the dispersion relation to obtain
In a quasineutral hydrogen plasma, the additional constraint enforces the relation
![]() $\unicode[STIX]{x1D708}_{i}=1$
and we trivially recover equation (3.3) (e.g. Fried & Gould Reference Fried and Gould1961; Yegorenkov & Stepanov Reference Yegorenkov and Stepanov1988), which describes the plasma stability in the absence of density and temperature gradients and assuming
$\unicode[STIX]{x1D708}_{i}=1$
and we trivially recover equation (3.3) (e.g. Fried & Gould Reference Fried and Gould1961; Yegorenkov & Stepanov Reference Yegorenkov and Stepanov1988), which describes the plasma stability in the absence of density and temperature gradients and assuming
![]() $T_{i}=T_{e}$
$T_{i}=T_{e}$
This equation has an infinite number of solutions which can be of either the ion type with
![]() $\unicode[STIX]{x1D701}_{i}\geqslant 1$
and
$\unicode[STIX]{x1D701}_{i}\geqslant 1$
and
![]() $\unicode[STIX]{x1D701}_{e}\ll 1,$
or the electron type with
$\unicode[STIX]{x1D701}_{e}\ll 1,$
or the electron type with
![]() $\unicode[STIX]{x1D701}_{e}\geqslant 1.$
Mishchenko et al. (Reference Mishchenko, Zocco, Helander and Könies2018b
) investigate these sound wave solutions for quasineutral hydrogen plasmas, electron–positron plasmas and electron–positron–ion plasmas.
$\unicode[STIX]{x1D701}_{e}\geqslant 1.$
Mishchenko et al. (Reference Mishchenko, Zocco, Helander and Könies2018b
) investigate these sound wave solutions for quasineutral hydrogen plasmas, electron–positron plasmas and electron–positron–ion plasmas.
For non-neutral plasmas, we can make analytical progress for sound waves of the ion type, satisfying
![]() $\unicode[STIX]{x1D701}_{i}\gg 1$
and
$\unicode[STIX]{x1D701}_{i}\gg 1$
and
![]() $\unicode[STIX]{x1D701}_{e}\ll 1$
. In this regime the following asymptotic forms of the plasma dispersion function can be used:
$\unicode[STIX]{x1D701}_{e}\ll 1$
. In this regime the following asymptotic forms of the plasma dispersion function can be used:
which lead to the approximated dispersion relation for sound waves of the ion type
For simplicity, we will neglect FLR effects implying
![]() $\unicode[STIX]{x1D6E4}_{0i}=1.$
We are also at liberty to neglect the small contributions
$\unicode[STIX]{x1D6E4}_{0i}=1.$
We are also at liberty to neglect the small contributions
![]() $1/(4\unicode[STIX]{x1D701}_{i}^{2})\ll 1$
relative to the other terms. We then obtain the dispersion relation in the form
$1/(4\unicode[STIX]{x1D701}_{i}^{2})\ll 1$
relative to the other terms. We then obtain the dispersion relation in the form
Using the notation
![]() $\unicode[STIX]{x1D701}=x-\text{i}y$
and assuming
$\unicode[STIX]{x1D701}=x-\text{i}y$
and assuming
![]() $x=\pm (y+\unicode[STIX]{x1D6E5})$
with
$x=\pm (y+\unicode[STIX]{x1D6E5})$
with
![]() $\unicode[STIX]{x1D6E5}\ll 1$
, we arrive at
$\unicode[STIX]{x1D6E5}\ll 1$
, we arrive at
From this, we can write down an infinite family of solutions for sound waves of the ion type as
One sees that
![]() $\unicode[STIX]{x1D6E5}_{m}$
increases with
$\unicode[STIX]{x1D6E5}_{m}$
increases with
![]() $\unicode[STIX]{x1D708}_{i}>1$
, i.e. the real part of the frequency increases at
$\unicode[STIX]{x1D708}_{i}>1$
, i.e. the real part of the frequency increases at
![]() $\unicode[STIX]{x1D708}_{i}>1$
. The condition
$\unicode[STIX]{x1D708}_{i}>1$
. The condition
![]() $\unicode[STIX]{x1D6E5}_{m}\ll 1$
is violated when
$\unicode[STIX]{x1D6E5}_{m}\ll 1$
is violated when
![]() $\unicode[STIX]{x1D708}_{i}$
is large enough and the asymptotic relations hitherto employed are rendered invalid.
$\unicode[STIX]{x1D708}_{i}$
is large enough and the asymptotic relations hitherto employed are rendered invalid.
The waves described above are simply Landau damped sound waves propagating in an electron–ion plasma slab and are stable in both non-neutral and quasineutral plasmas, a well-established result in the quasineutral case. We note that the calculations in this section are independent of the species charge and hence the same Landau damped sound waves can propagate in an electron–antiproton plasma slab. This idea has been further explored by Dubin (Reference Dubin2010) who found that such waves can propagate with only very weak Landau damping provided that the density of the heavy species is large compared to that of the light species i.e.
![]() $\unicode[STIX]{x1D708}_{i}\gg 1.$
In the analytic model considered here, such an ordering renders the previous assumptions invalid and the asymptotic limit analysis breaks down.
$\unicode[STIX]{x1D708}_{i}\gg 1.$
In the analytic model considered here, such an ordering renders the previous assumptions invalid and the asymptotic limit analysis breaks down.
However, one can of course perform a similar analysis for the case where the species fraction of the large species is much greater than one. i.e.
![]() $\unicode[STIX]{x1D708}_{i}\gg 1.$
In this case, one employs the notation
$\unicode[STIX]{x1D708}_{i}\gg 1.$
In this case, one employs the notation
![]() $\unicode[STIX]{x1D709}=x(1-\text{i}\unicode[STIX]{x1D6E5}).$
We obtain the results
$\unicode[STIX]{x1D709}=x(1-\text{i}\unicode[STIX]{x1D6E5}).$
We obtain the results
where the lowest-order mode,
![]() $m=1,$
corresponds to the sound wave solution. Hence, we obtain the result that indeed for sufficiently large ion fraction, sound waves can propagate in electron–antiproton plasmas with only weak Landau damping, in qualitative agreement with Dubin (Reference Dubin2010).
$m=1,$
corresponds to the sound wave solution. Hence, we obtain the result that indeed for sufficiently large ion fraction, sound waves can propagate in electron–antiproton plasmas with only weak Landau damping, in qualitative agreement with Dubin (Reference Dubin2010).
4 Density-gradient-driven modes
We now turn out attention to unstable modes by allowing gradients in the plasma profiles. Universal modes are plasma modes which can be driven unstable by density gradients. For simplicity we assume throughout this section that the temperature profiles of all species are flat and equal. We will later relax this constraint when we consider modes driven by temperature gradients. We will also once again focus our attention on electron–ion plasmas to highlight the difference between quasineutral and non-neutral plasmas in a perhaps more familiar setting.
The dispersion relation in two-component non-neutral plasma (one light species and one heavy) has the form,
where, as introduced above, we have employed the notation
![]() $\unicode[STIX]{x1D708}_{a}=n_{a}/n_{e}$
for each species. We once again highlight the difference between quasineutral plasmas, in which
$\unicode[STIX]{x1D708}_{a}=n_{a}/n_{e}$
for each species. We once again highlight the difference between quasineutral plasmas, in which
![]() $\unicode[STIX]{x1D708}_{i}=1,$
and the non-neutral plasmas considered here where
$\unicode[STIX]{x1D708}_{i}=1,$
and the non-neutral plasmas considered here where
![]() $\unicode[STIX]{x1D708}_{i}$
can be completely arbitrary. Taking the limit
$\unicode[STIX]{x1D708}_{i}$
can be completely arbitrary. Taking the limit
![]() $k_{\Vert }v_{\text{th}i}\ll \unicode[STIX]{x1D714}\ll k_{\Vert }v_{\text{th}e}$
we obtain the leading-order approximations to the plasma dispersion functions,
$k_{\Vert }v_{\text{th}i}\ll \unicode[STIX]{x1D714}\ll k_{\Vert }v_{\text{th}e}$
we obtain the leading-order approximations to the plasma dispersion functions,
Hence to lowest order we obtain the dispersion relation
Solution of this equation for
![]() $\unicode[STIX]{x1D714}=\unicode[STIX]{x1D714}_{r}+\text{i}\unicode[STIX]{x1D6FE}$
assuming
$\unicode[STIX]{x1D714}=\unicode[STIX]{x1D714}_{r}+\text{i}\unicode[STIX]{x1D6FE}$
assuming
![]() $\unicode[STIX]{x1D6FE}\ll \unicode[STIX]{x1D714}_{r}$
is
$\unicode[STIX]{x1D6FE}\ll \unicode[STIX]{x1D714}_{r}$
is
One sees that the frequency is determined by the density gradient of the heavy species (ions) and the growth rate by the density gradient of the light species (electrons). One requires density gradients of both species to have an instability, implying that both
![]() $\unicode[STIX]{x1D714}_{r}\sim |\unicode[STIX]{x1D714}_{\ast i}|>0$
and
$\unicode[STIX]{x1D714}_{r}\sim |\unicode[STIX]{x1D714}_{\ast i}|>0$
and
![]() $\unicode[STIX]{x1D6FE}\sim \unicode[STIX]{x1D714}_{\ast e}-\unicode[STIX]{x1D714}_{r}>0$
.
$\unicode[STIX]{x1D6FE}\sim \unicode[STIX]{x1D714}_{\ast e}-\unicode[STIX]{x1D714}_{r}>0$
.
In the quasineutral case, the additional restriction of
![]() $\unicode[STIX]{x1D708}_{e}+\unicode[STIX]{x1D708}_{i}=2$
renders the growth rate monotonic as in Mishchenko et al. (Reference Mishchenko, Zocco, Helander and Könies2018b
). This behaviour is shown in the numerical solution of the dispersion relation (2.17) in the quasineutral case shown in figure 1 where we plot the growth rate and frequency of the universal mode as a function of
$\unicode[STIX]{x1D708}_{e}+\unicode[STIX]{x1D708}_{i}=2$
renders the growth rate monotonic as in Mishchenko et al. (Reference Mishchenko, Zocco, Helander and Könies2018b
). This behaviour is shown in the numerical solution of the dispersion relation (2.17) in the quasineutral case shown in figure 1 where we plot the growth rate and frequency of the universal mode as a function of
![]() $\unicode[STIX]{x1D705}_{ni}$
. Here, we use the parameters
$\unicode[STIX]{x1D705}_{ni}$
. Here, we use the parameters
![]() $\unicode[STIX]{x1D706}_{D}/\unicode[STIX]{x1D70C}_{i}=\unicode[STIX]{x1D705}_{Te}\unicode[STIX]{x1D70C}_{i}=\unicode[STIX]{x1D705}_{Tp}\unicode[STIX]{x1D70C}_{i}=\unicode[STIX]{x1D705}_{Ti}=0,$
$\unicode[STIX]{x1D706}_{D}/\unicode[STIX]{x1D70C}_{i}=\unicode[STIX]{x1D705}_{Te}\unicode[STIX]{x1D70C}_{i}=\unicode[STIX]{x1D705}_{Tp}\unicode[STIX]{x1D70C}_{i}=\unicode[STIX]{x1D705}_{Ti}=0,$
![]() $k_{y}\unicode[STIX]{x1D70C}_{i}=2,k_{\Vert }\unicode[STIX]{x1D70C}_{i}=7.4\times 10^{-4}$
with the notation
$k_{y}\unicode[STIX]{x1D70C}_{i}=2,k_{\Vert }\unicode[STIX]{x1D70C}_{i}=7.4\times 10^{-4}$
with the notation
We note that in the quasineutral case we are forced to set the electron density gradient through the quasineutrality condition
![]() $\unicode[STIX]{x1D708}_{e}\unicode[STIX]{x1D714}_{\star e}+\unicode[STIX]{x1D708}_{i}\unicode[STIX]{x1D714}_{\star i}=0.$
In the non-neutral case however, we have another free parameter in that we may set
$\unicode[STIX]{x1D708}_{e}\unicode[STIX]{x1D714}_{\star e}+\unicode[STIX]{x1D708}_{i}\unicode[STIX]{x1D714}_{\star i}=0.$
In the non-neutral case however, we have another free parameter in that we may set
![]() $\unicode[STIX]{x1D705}_{ni}$
and
$\unicode[STIX]{x1D705}_{ni}$
and
![]() $\unicode[STIX]{x1D705}_{ne}$
independently.
$\unicode[STIX]{x1D705}_{ne}$
independently.
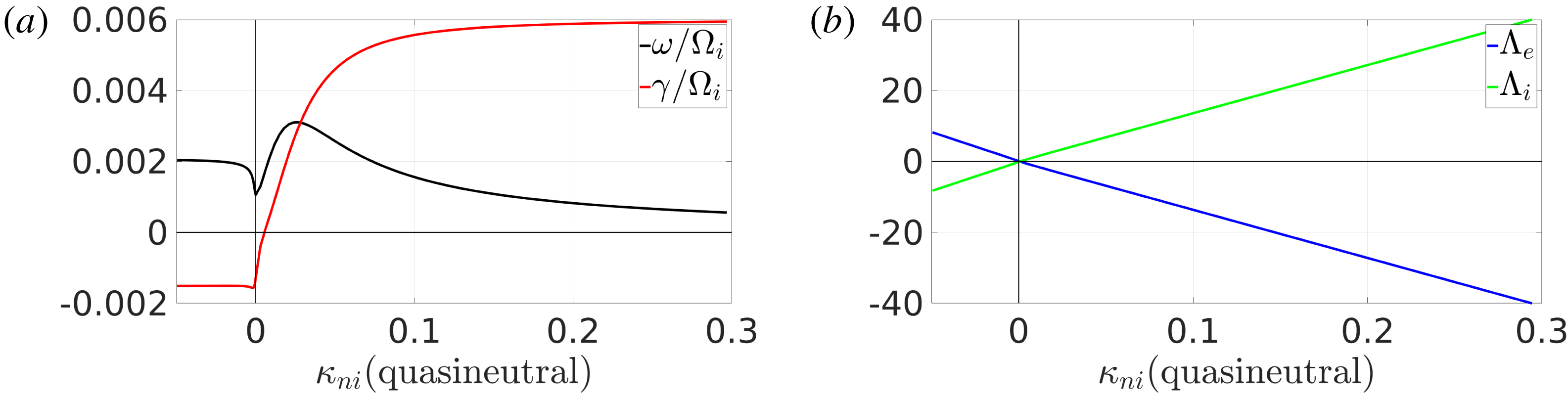
Figure 1. The frequency
![]() $\unicode[STIX]{x1D714},$
and growth rate
$\unicode[STIX]{x1D714},$
and growth rate
![]() $\unicode[STIX]{x1D6FE},$
of the universal mode (a) and the associated scaled quasilinear particle fluxes as defined by (2.24) (b) as a function of the ion density gradient
$\unicode[STIX]{x1D6FE},$
of the universal mode (a) and the associated scaled quasilinear particle fluxes as defined by (2.24) (b) as a function of the ion density gradient
![]() $\unicode[STIX]{x1D705}_{ni}$
in a quasineutral electron–ion plasma. One sees that the ion density gradient must be larger than some threshold for the mode to become unstable. The growth rate increases monotonically with the ion density gradient. Parameters as given in the text.
$\unicode[STIX]{x1D705}_{ni}$
in a quasineutral electron–ion plasma. One sees that the ion density gradient must be larger than some threshold for the mode to become unstable. The growth rate increases monotonically with the ion density gradient. Parameters as given in the text.
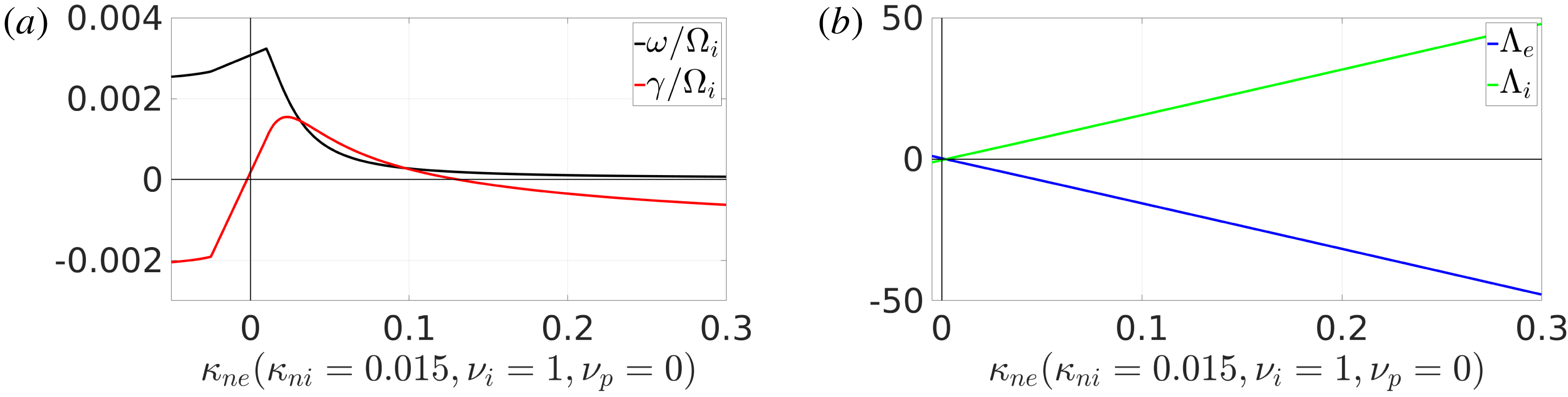
Figure 2. The frequency
![]() $\unicode[STIX]{x1D714},$
and growth rate
$\unicode[STIX]{x1D714},$
and growth rate
![]() $\unicode[STIX]{x1D6FE},$
of the universal mode (a) and the associated scaled quasilinear particle fluxes (b) as a function of the electron density gradient
$\unicode[STIX]{x1D6FE},$
of the universal mode (a) and the associated scaled quasilinear particle fluxes (b) as a function of the electron density gradient
![]() $\unicode[STIX]{x1D705}_{ne}$
in a non-neutral electron–ion plasma. The dependence of the growth rate on the density gradient becomes non-monotonic so that a second threshold at large density gradients appears. Parameters as given in the text.
$\unicode[STIX]{x1D705}_{ne}$
in a non-neutral electron–ion plasma. The dependence of the growth rate on the density gradient becomes non-monotonic so that a second threshold at large density gradients appears. Parameters as given in the text.

Figure 3. The frequency
![]() $\unicode[STIX]{x1D714},$
and growth rate
$\unicode[STIX]{x1D714},$
and growth rate
![]() $\unicode[STIX]{x1D6FE},$
of the universal mode (a) and the associated scaled quasilinear particle fluxes (b) as a function of the ion density gradient
$\unicode[STIX]{x1D6FE},$
of the universal mode (a) and the associated scaled quasilinear particle fluxes (b) as a function of the ion density gradient
![]() $\unicode[STIX]{x1D705}_{ni}$
in a non-neutral electron–ion plasma. The dependence of the growth rate on the density gradient becomes non-monotonic so that a second threshold at large density gradients appears. Parameters as given in the text.
$\unicode[STIX]{x1D705}_{ni}$
in a non-neutral electron–ion plasma. The dependence of the growth rate on the density gradient becomes non-monotonic so that a second threshold at large density gradients appears. Parameters as given in the text.

Figure 4. The frequency
![]() $\unicode[STIX]{x1D714},$
and growth rate
$\unicode[STIX]{x1D714},$
and growth rate
![]() $\unicode[STIX]{x1D6FE},$
of the universal mode (a) and the associated scaled quasilinear particle fluxes (b) as a function of the antiproton density gradient
$\unicode[STIX]{x1D6FE},$
of the universal mode (a) and the associated scaled quasilinear particle fluxes (b) as a function of the antiproton density gradient
![]() $\unicode[STIX]{x1D705}_{ni}$
in a non-neutral electron–antiproton plasma. The dependence of the growth rate on the density gradient becomes non-monotonic so that a second threshold at large density gradients appears. Parameters as given in the text.
$\unicode[STIX]{x1D705}_{ni}$
in a non-neutral electron–antiproton plasma. The dependence of the growth rate on the density gradient becomes non-monotonic so that a second threshold at large density gradients appears. Parameters as given in the text.
As such, in non-neutral plasmas, the behaviour of the instability is more interesting. We have adopted the convention that,
![]() $\unicode[STIX]{x1D714}_{\star i}<0$
and hence one expects the frequency of the universal modes to remain positive as the density profile steepens. This result lead to a monotonic growth rate in a quasineutral plasma as the growth rate was proportional to
$\unicode[STIX]{x1D714}_{\star i}<0$
and hence one expects the frequency of the universal modes to remain positive as the density profile steepens. This result lead to a monotonic growth rate in a quasineutral plasma as the growth rate was proportional to
![]() $-\unicode[STIX]{x1D714}_{r}\unicode[STIX]{x1D714}_{\star i}.$
In non-neutral plasmas, however, the growth rate depends nonlinearly on the frequency and is proportional to
$-\unicode[STIX]{x1D714}_{r}\unicode[STIX]{x1D714}_{\star i}.$
In non-neutral plasmas, however, the growth rate depends nonlinearly on the frequency and is proportional to
![]() $\unicode[STIX]{x1D714}_{r}(\unicode[STIX]{x1D714}_{\star e}-\unicode[STIX]{x1D714}_{r}),$
so that if
$\unicode[STIX]{x1D714}_{r}(\unicode[STIX]{x1D714}_{\star e}-\unicode[STIX]{x1D714}_{r}),$
so that if
![]() $\unicode[STIX]{x1D714}_{r}>\unicode[STIX]{x1D714}_{\star e}$
the growth rate decreases, which leads to a second stability threshold for the universal mode. This can be seen in figures 2 and 3 where the full dispersion relation is solved for the same parameters as above but with the assumption of quasineutrality relaxed. One would need to revisit the asymptotic analysis and include resonant contributions etc. to find the analytic stability threshold, however this can easily be found numerically when required. It is important to note that no such second stability threshold exists in standard quasineutral plasmas and that this feature is unique to non-neutral plasmas. We see a similar pattern with a sufficiently large density gradient stabilising the universal mode for electron–antiproton plasmas as shown in figure 4. It is interesting to note that instability in antiproton–electron plasmas requires
$\unicode[STIX]{x1D714}_{r}>\unicode[STIX]{x1D714}_{\star e}$
the growth rate decreases, which leads to a second stability threshold for the universal mode. This can be seen in figures 2 and 3 where the full dispersion relation is solved for the same parameters as above but with the assumption of quasineutrality relaxed. One would need to revisit the asymptotic analysis and include resonant contributions etc. to find the analytic stability threshold, however this can easily be found numerically when required. It is important to note that no such second stability threshold exists in standard quasineutral plasmas and that this feature is unique to non-neutral plasmas. We see a similar pattern with a sufficiently large density gradient stabilising the universal mode for electron–antiproton plasmas as shown in figure 4. It is interesting to note that instability in antiproton–electron plasmas requires
![]() $\unicode[STIX]{x1D705}_{ni}\unicode[STIX]{x1D705}_{ne}<0,$
this condition is only necessary for plasmas where each species has the same sign of charge. This result agrees with those obtained by Dubin (Reference Dubin2010) using an analytic model in a cylindrical geometry. It is also interesting to note that these modes have a different sign of frequency compared to the modes in plasmas where the different species have different signs of charge.
$\unicode[STIX]{x1D705}_{ni}\unicode[STIX]{x1D705}_{ne}<0,$
this condition is only necessary for plasmas where each species has the same sign of charge. This result agrees with those obtained by Dubin (Reference Dubin2010) using an analytic model in a cylindrical geometry. It is also interesting to note that these modes have a different sign of frequency compared to the modes in plasmas where the different species have different signs of charge.
The scaled fluxes
![]() $\unicode[STIX]{x1D6EC}_{a}$
are also shown in figures 1–4. We immediately note once again by inspection that the quasilinear transport is ambipolar, as proven previously.
$\unicode[STIX]{x1D6EC}_{a}$
are also shown in figures 1–4. We immediately note once again by inspection that the quasilinear transport is ambipolar, as proven previously.
5 ETG instability
We now turn our attention to the case where temperature gradients are present in the plasma, this is likely to be of importance to the PAX/APEX investigations. In the aforementioned experiments, it is planned to confine an electron–positron plasma in a vacuum vessel using a levitated coil. In order to accomplish this goal, the electrons are to be injected with an electron gun whereas the positrons will be supplied from the research neutron source at the Technical University of Munich. This separate injection may afford different temperature profiles to the two species.
For simplicity we will now consider flat density profiles. We will find it convenient to define
![]() $\unicode[STIX]{x1D714}_{Ta}=\unicode[STIX]{x1D702}_{a}\unicode[STIX]{x1D714}_{\star a}=k_{y}T_{a}/(e_{a}B)\,\text{d}\ln T_{a}/\text{d}x,$
which is finite also at zero density gradient.
$\unicode[STIX]{x1D714}_{Ta}=\unicode[STIX]{x1D702}_{a}\unicode[STIX]{x1D714}_{\star a}=k_{y}T_{a}/(e_{a}B)\,\text{d}\ln T_{a}/\text{d}x,$
which is finite also at zero density gradient.
We will allow symmetry breaking not only through relaxation of the quasineutrality condition, but also by allowing each plasma species to have different temperature profiles. To this end, we introduce the notation
where
![]() $\unicode[STIX]{x1D708}_{a}=n_{a}/n_{e}$
and
$\unicode[STIX]{x1D708}_{a}=n_{a}/n_{e}$
and
![]() $\unicode[STIX]{x1D70F}_{a}=T_{a}/T_{e}.$
It is important to note that quasineutral plasmas satisfy both
$\unicode[STIX]{x1D70F}_{a}=T_{a}/T_{e}.$
It is important to note that quasineutral plasmas satisfy both
![]() $\sum _{a}\unicode[STIX]{x1D708}_{a}=2$
and
$\sum _{a}\unicode[STIX]{x1D708}_{a}=2$
and
![]() $\sum _{a}\hat{\unicode[STIX]{x1D708}}_{a}=2$
whereas in non-neutral plasmas these quantities are both arbitrary. If the temperatures of all species are equal
$\sum _{a}\hat{\unicode[STIX]{x1D708}}_{a}=2$
whereas in non-neutral plasmas these quantities are both arbitrary. If the temperatures of all species are equal
![]() $(\unicode[STIX]{x1D70F}_{a}=1)$
in such plasmas then
$(\unicode[STIX]{x1D70F}_{a}=1)$
in such plasmas then
![]() $\hat{\unicode[STIX]{x1D708}}_{a}=\unicode[STIX]{x1D708}_{a}.$
$\hat{\unicode[STIX]{x1D708}}_{a}=\unicode[STIX]{x1D708}_{a}.$
We seek to use our machinery to examine the behaviour of electron and positron temperature-gradient-driven modes. Using this notation and restricting our attention to the case where the only gradients present are electron and positron temperature gradients, the dispersion relation reduces to
We assume that
![]() $k_{\bot }\unicode[STIX]{x1D70C}_{i}\gg 1$
but
$k_{\bot }\unicode[STIX]{x1D70C}_{i}\gg 1$
but
![]() $k_{\bot }\unicode[STIX]{x1D70C}_{e,p}\ll 1,$
which yields
$k_{\bot }\unicode[STIX]{x1D70C}_{e,p}\ll 1,$
which yields
and also make the assumption of large frequencies
![]() $\unicode[STIX]{x1D714}\gg k_{\Vert }v_{\text{th}(e,p)},$
allowing us to use an asymptotic form of the plasma dispersion function. Namely, we can make use of the relations
$\unicode[STIX]{x1D714}\gg k_{\Vert }v_{\text{th}(e,p)},$
allowing us to use an asymptotic form of the plasma dispersion function. Namely, we can make use of the relations
where the second expansion follows immediately from the recurrence relation
![]() $Z_{2}(\unicode[STIX]{x1D701})=\unicode[STIX]{x1D701}+\unicode[STIX]{x1D701}^{2}Z_{0}(\unicode[STIX]{x1D701})$
which itself follows straightforwardly from (2.14).
$Z_{2}(\unicode[STIX]{x1D701})=\unicode[STIX]{x1D701}+\unicode[STIX]{x1D701}^{2}Z_{0}(\unicode[STIX]{x1D701})$
which itself follows straightforwardly from (2.14).
These simplifications reduce the dispersion relation in the leading order to
This dispersion relation is valid in plasmas of arbitrary neutrality since the ion response is negligible due to
![]() $\unicode[STIX]{x1D6E4}_{0i}\approx 0$
at large
$\unicode[STIX]{x1D6E4}_{0i}\approx 0$
at large
![]() $k_{\bot }\unicode[STIX]{x1D70C}_{i}$
. One can solve this leading-order approximation to the dispersion relation analytically to obtain the unstable branch
$k_{\bot }\unicode[STIX]{x1D70C}_{i}$
. One can solve this leading-order approximation to the dispersion relation analytically to obtain the unstable branch
This equation immediately leads to the first interesting result that even pure electron plasmas can sustain unstable electron temperature-gradient-driven (ETG) modes. This is easily seen by simply noting even when
![]() $\unicode[STIX]{x1D708}_{i}=\unicode[STIX]{x1D708}_{p}=0$
the unstable branch still exists.
$\unicode[STIX]{x1D708}_{i}=\unicode[STIX]{x1D708}_{p}=0$
the unstable branch still exists.
Another interesting result here is the existence of such modes in pair plasma with no ion contamination. In Mishchenko et al. (Reference Mishchenko, Zocco, Helander and Könies2018b
) it was found that temperature-gradient-driven instabilities can exist in pair plasmas in a slab only if the temperatures of the two species differed. However, in non-neutral plasmas the ETG mode can also be unstable even in a pure pair plasma where the electrons and positrons have the same temperature profiles provided that
![]() $\unicode[STIX]{x1D708}_{p}\neq 1.$
Again this is also seen from the asymptotic solution to the dispersion relation.
$\unicode[STIX]{x1D708}_{p}\neq 1.$
Again this is also seen from the asymptotic solution to the dispersion relation.
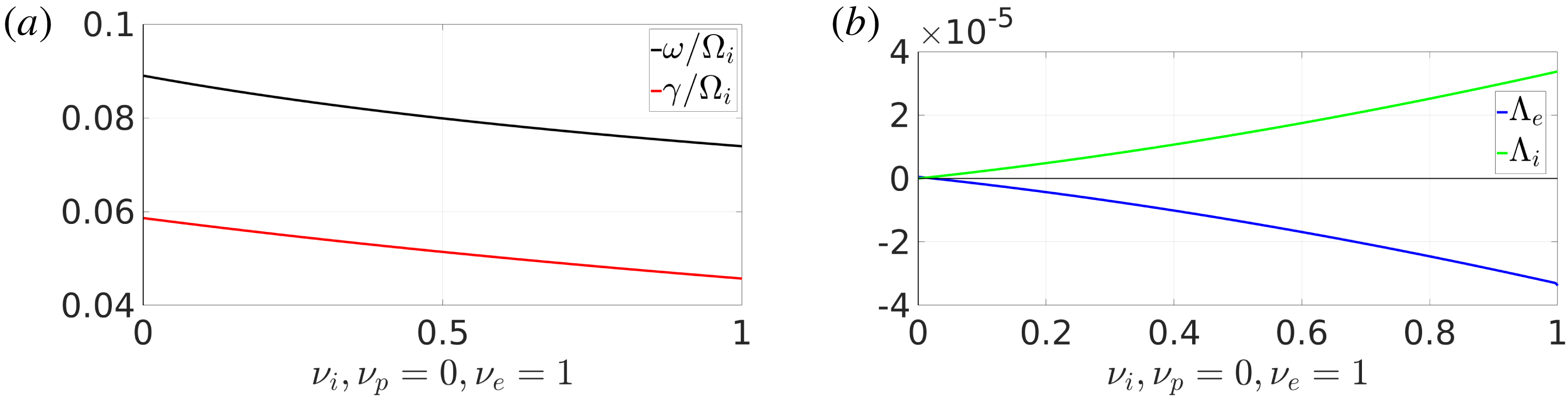
Figure 5. The frequency
![]() $\unicode[STIX]{x1D714},$
and the growth rate
$\unicode[STIX]{x1D714},$
and the growth rate
![]() $\unicode[STIX]{x1D6FE},$
of the ETG instability (a) and the associated scaled quasilinear particle fluxes (b) as a function of ion fraction
$\unicode[STIX]{x1D6FE},$
of the ETG instability (a) and the associated scaled quasilinear particle fluxes (b) as a function of ion fraction
![]() $\unicode[STIX]{x1D708}_{i},$
in a non-neutral electron–ion plasma. Parameters as given in the text.
$\unicode[STIX]{x1D708}_{i},$
in a non-neutral electron–ion plasma. Parameters as given in the text.

Figure 6. The frequency
![]() $\unicode[STIX]{x1D714},$
and the growth rate
$\unicode[STIX]{x1D714},$
and the growth rate
![]() $\unicode[STIX]{x1D6FE},$
of the ETG instability (a) and the associated scaled quasilinear particle fluxes (b) as a function of the positron fraction
$\unicode[STIX]{x1D6FE},$
of the ETG instability (a) and the associated scaled quasilinear particle fluxes (b) as a function of the positron fraction
![]() $\unicode[STIX]{x1D708}_{p},$
in non-neutral pair plasma. We note that in a non-neutral pure pair plasma (i.e. with no ion contamination) it is still possible to have temperature-gradient-driven instabilities as there is no requirement for the electron and positron contributions to cancel. Parameters as given in the text.
$\unicode[STIX]{x1D708}_{p},$
in non-neutral pair plasma. We note that in a non-neutral pure pair plasma (i.e. with no ion contamination) it is still possible to have temperature-gradient-driven instabilities as there is no requirement for the electron and positron contributions to cancel. Parameters as given in the text.

Figure 7. The frequency,
![]() $\unicode[STIX]{x1D714},$
and the growth rate
$\unicode[STIX]{x1D714},$
and the growth rate
![]() $\unicode[STIX]{x1D6FE},$
of the PTG instability (a) and the associated scaled quasilinear particle fluxes (b) as a function of the positron fraction
$\unicode[STIX]{x1D6FE},$
of the PTG instability (a) and the associated scaled quasilinear particle fluxes (b) as a function of the positron fraction
![]() $\unicode[STIX]{x1D708}_{p},$
in non-neutral pair plasma. We note that in a non-neutral pure pair plasma (i.e. with no ion contamination) it is still possible to have temperature-gradient-driven instabilities as there is no requirement for the electron and positron contributions to cancel. Parameters as given in the text.
$\unicode[STIX]{x1D708}_{p},$
in non-neutral pair plasma. We note that in a non-neutral pure pair plasma (i.e. with no ion contamination) it is still possible to have temperature-gradient-driven instabilities as there is no requirement for the electron and positron contributions to cancel. Parameters as given in the text.

Figure 8. The frequency,
![]() $\unicode[STIX]{x1D714},$
and the growth rate
$\unicode[STIX]{x1D714},$
and the growth rate
![]() $\unicode[STIX]{x1D6FE},$
of the ETG instability (a) and the associated scaled quasilinear particle fluxes (b) as a function of the antiproton fraction
$\unicode[STIX]{x1D6FE},$
of the ETG instability (a) and the associated scaled quasilinear particle fluxes (b) as a function of the antiproton fraction
![]() $\unicode[STIX]{x1D708}_{i},$
in non-neutral electron–antiproton plasma. Parameters as given in the text.
$\unicode[STIX]{x1D708}_{i},$
in non-neutral electron–antiproton plasma. Parameters as given in the text.
These behaviours are clearly seen in figures 5–7 where the full dispersion relation (2.17) is solved for the parameters
![]() $\unicode[STIX]{x1D706}_{D}/\unicode[STIX]{x1D70C}_{i}=0.1,\unicode[STIX]{x1D705}_{Te}\unicode[STIX]{x1D70C}_{i}=\unicode[STIX]{x1D705}_{Tp}\unicode[STIX]{x1D70C}_{i}=0.1,\unicode[STIX]{x1D705}_{Ti}=0,k_{y}\unicode[STIX]{x1D70C}_{i}=12$
and
$\unicode[STIX]{x1D706}_{D}/\unicode[STIX]{x1D70C}_{i}=0.1,\unicode[STIX]{x1D705}_{Te}\unicode[STIX]{x1D70C}_{i}=\unicode[STIX]{x1D705}_{Tp}\unicode[STIX]{x1D70C}_{i}=0.1,\unicode[STIX]{x1D705}_{Ti}=0,k_{y}\unicode[STIX]{x1D70C}_{i}=12$
and
![]() $k_{\Vert }\unicode[STIX]{x1D70C}_{i}=7.4\times 10^{-4},$
With different numbers and types of species being shown in each figure.
$k_{\Vert }\unicode[STIX]{x1D70C}_{i}=7.4\times 10^{-4},$
With different numbers and types of species being shown in each figure.
For non-neutral electron–ion plasmas, the ETG mode still exists and shows little deviation as the ion fraction is varied. This is seen in figure 5 where we note that ETG modes are unstable through a large swathe of ion fractions ranging from a quasineutral electron–ion plasma (right most point) through to a pure electron plasma (left most point). Again we see from this solution of the full dispersion relation that unstable ETG modes can exist even in pure electron plasmas. The ETG mode can also be unstable in non-neutral pair plasmas for
![]() $\unicode[STIX]{x1D708}_{p}<\unicode[STIX]{x1D708}_{e}$
(see figure 6) and the positron-temperature-gradient (PTG) driven instability can appear for
$\unicode[STIX]{x1D708}_{p}<\unicode[STIX]{x1D708}_{e}$
(see figure 6) and the positron-temperature-gradient (PTG) driven instability can appear for
![]() $\unicode[STIX]{x1D708}_{p}>\unicode[STIX]{x1D708}_{e}$
(see figure 7). This PTG mode propagates in the opposite direction to the ETG modes.
$\unicode[STIX]{x1D708}_{p}>\unicode[STIX]{x1D708}_{e}$
(see figure 7). This PTG mode propagates in the opposite direction to the ETG modes.
Similarly the ETG mode also exists in electron–antiproton plasmas as shown in figure 8. The left most point in this figures of corresponds to a pure electron plasma is in agreement with the pure electron plasma limit of the previous figures.
Interestingly, both the ETG and PTG modes are stable for pair plasmas which are ‘close’ to quasineutrality, this is easily seen in on figure 6(b) and figure 7(a) where the growth rate is negative.
One area of investigation which is important experimentally is the effect of large Debye length on this class of instabilities. In fusion plasmas this effect is usually negligible as the Debye length is much smaller than the ion Larmor radius for fusion relevant parameters. However, for the pair plasma experiment under construction, this will not be the case. The Debye length of such plasmas is expected to become comparable to the proton gyroradius. One can see from (5.6) that large Debye length can have a strongly stabilising effect on the ETG and PTG instabilities in a non-neutral pair plasma.
Once again we note that the quasilinear particle fluxes obtained numerically are ambipolar. Furthermore, focussing our attention on figure 6 we can obtain a useful sanity check on our model. We note that, even though the growth rate is large, the scaled particle flux (and hence the actual quasilinear particle flux) of both species tends to zero as
![]() $\unicode[STIX]{x1D708}_{p}\rightarrow 0.$
This is again a consequence of ambipolarity.
$\unicode[STIX]{x1D708}_{p}\rightarrow 0.$
This is again a consequence of ambipolarity.
6 ITG instability
In analogy to the ETG instability, the ITG mode can exist in non-neutral plasma with a sufficiently large ion fraction
![]() $\unicode[STIX]{x1D708}_{i}>\unicode[STIX]{x1D708}_{e}$
, see figure 9. Interestingly, the ITG mode needs some finite fraction of electrons to be unstable, in contrast to the ETG instability which we found could also exist in pure electron plasma and did not need a finite ion or positron fraction.
$\unicode[STIX]{x1D708}_{i}>\unicode[STIX]{x1D708}_{e}$
, see figure 9. Interestingly, the ITG mode needs some finite fraction of electrons to be unstable, in contrast to the ETG instability which we found could also exist in pure electron plasma and did not need a finite ion or positron fraction.
We restrict our attention to a non-neutral electron–ion plasma where the only gradients present are now ion temperature gradients. The dispersion relation becomes
We consider the long wavelength limit
![]() $\unicode[STIX]{x1D6E4}_{0a}=\unicode[STIX]{x1D6E4}_{\star a}=1$
for all particle species. For the ITG instability, we can assume that
$\unicode[STIX]{x1D6E4}_{0a}=\unicode[STIX]{x1D6E4}_{\star a}=1$
for all particle species. For the ITG instability, we can assume that
![]() $k_{\Vert }v_{\text{th}i}\ll \unicode[STIX]{x1D714}\ll k_{\Vert }v_{\text{th}(e,p)}.$
Then, the plasma dispersion function can be expanded as
$k_{\Vert }v_{\text{th}i}\ll \unicode[STIX]{x1D714}\ll k_{\Vert }v_{\text{th}(e,p)}.$
Then, the plasma dispersion function can be expanded as
To leading order, we obtain the dispersion relation
Noting that by convention
![]() $\unicode[STIX]{x1D714}_{Ti}<0,$
we obtain the unstable branch of the ITG mode
$\unicode[STIX]{x1D714}_{Ti}<0,$
we obtain the unstable branch of the ITG mode
We can see immediately from this equation that the ITG frequency is negative, as expected. One also sees, exactly the same as in the quasineutral case, the factor
![]() $(\hat{\unicode[STIX]{x1D708}}_{i}\unicode[STIX]{x1D714}_{Ti})^{1/3}$
appearing in the numerator of the growth rate. However, the dependence of the growth rate on
$(\hat{\unicode[STIX]{x1D708}}_{i}\unicode[STIX]{x1D714}_{Ti})^{1/3}$
appearing in the numerator of the growth rate. However, the dependence of the growth rate on
![]() $(\hat{\unicode[STIX]{x1D708}}_{i}\unicode[STIX]{x1D714}_{Ti})^{1/3}$
is no longer monotonic as we are no longer restricted to the range
$(\hat{\unicode[STIX]{x1D708}}_{i}\unicode[STIX]{x1D714}_{Ti})^{1/3}$
is no longer monotonic as we are no longer restricted to the range
![]() $\unicode[STIX]{x1D708}_{i}\in [0,1]$
as we were in the quasineutral case. One can also see that the ITG mode is stabilised for sufficiently large ion fraction, this can be seen from the asymptotic solution of the dispersion relation. This behaviour is seen in the numerical solution of the full dispersion relation (2.17) as shown in figure 9. Here, the dispersion relation is solved for the parameters
$\unicode[STIX]{x1D708}_{i}\in [0,1]$
as we were in the quasineutral case. One can also see that the ITG mode is stabilised for sufficiently large ion fraction, this can be seen from the asymptotic solution of the dispersion relation. This behaviour is seen in the numerical solution of the full dispersion relation (2.17) as shown in figure 9. Here, the dispersion relation is solved for the parameters
![]() $\unicode[STIX]{x1D706}_{D}/\unicode[STIX]{x1D70C}_{i}=0.1,$
$\unicode[STIX]{x1D706}_{D}/\unicode[STIX]{x1D70C}_{i}=0.1,$
![]() $\unicode[STIX]{x1D705}_{T_{i}}\unicode[STIX]{x1D70C}_{i}=\unicode[STIX]{x1D705}_{T_{e}}\unicode[STIX]{x1D70C}_{i}=0.02,\unicode[STIX]{x1D705}_{n(i,e)}=0,k_{y}\unicode[STIX]{x1D70C}_{i}=0.3,k_{\Vert }\unicode[STIX]{x1D70C}_{i}=7.4\times 10^{-4}.$
$\unicode[STIX]{x1D705}_{T_{i}}\unicode[STIX]{x1D70C}_{i}=\unicode[STIX]{x1D705}_{T_{e}}\unicode[STIX]{x1D70C}_{i}=0.02,\unicode[STIX]{x1D705}_{n(i,e)}=0,k_{y}\unicode[STIX]{x1D70C}_{i}=0.3,k_{\Vert }\unicode[STIX]{x1D70C}_{i}=7.4\times 10^{-4}.$
There is also non-monotonic behaviour displayed by the scaled quasilinear fluxes. As seen in figure 9 there is a change in the direction of particle transport for sufficiently large ion fraction.
The antiproton temperature-gradient instability in electron–antiproton plasmas can be seen in figure 10. It is interesting to note that frequency of these waves are positive, propagating in the opposite direction to ITG-driven waves in electron–ion plasmas. Similar to the ITG instability, a finite number of antiprotons are required for the modes to become unstable.
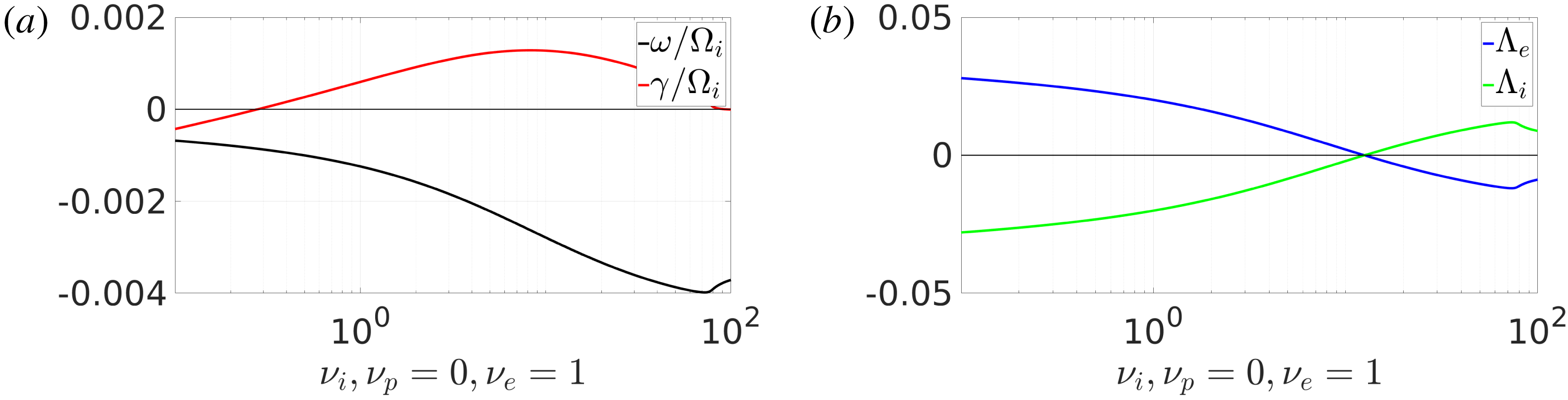
Figure 9. The frequency,
![]() $\unicode[STIX]{x1D714},$
and the growth rate
$\unicode[STIX]{x1D714},$
and the growth rate
![]() $\unicode[STIX]{x1D6FE},$
of the ITG instability (a) and associated scaled quasilinear particle fluxes (b) as a function of the ion fraction
$\unicode[STIX]{x1D6FE},$
of the ITG instability (a) and associated scaled quasilinear particle fluxes (b) as a function of the ion fraction
![]() $\unicode[STIX]{x1D708}_{i},$
in non-neutral electron–ion plasma. Parameters as given in the text.
$\unicode[STIX]{x1D708}_{i},$
in non-neutral electron–ion plasma. Parameters as given in the text.
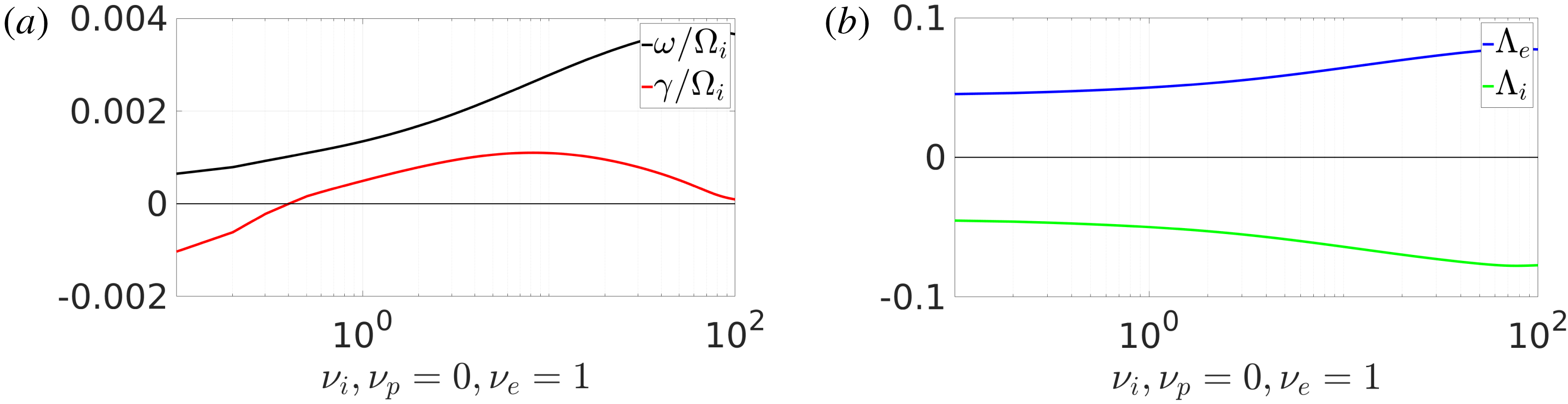
Figure 10. The frequency,
![]() $\unicode[STIX]{x1D714},$
and the growth rate
$\unicode[STIX]{x1D714},$
and the growth rate
![]() $\unicode[STIX]{x1D6FE},$
of the ITG instability (a) and associated scaled quasilinear particle fluxes (b) as a function of the ion fraction
$\unicode[STIX]{x1D6FE},$
of the ITG instability (a) and associated scaled quasilinear particle fluxes (b) as a function of the ion fraction
![]() $\unicode[STIX]{x1D708}_{i},$
in non-neutral electron–antiproton plasma. Parameters as given in the text.
$\unicode[STIX]{x1D708}_{i},$
in non-neutral electron–antiproton plasma. Parameters as given in the text.
7 Summary and discussion
In this paper, we have studied the gyrokinetic stability of non-neutral electron–positron–ion plasmas by solving, both analytically and numerically, the dispersion relation (2.17) in a slab geometry and relaxing the quasineutrality condition. It has been found that, much like their quasineutral counterparts, such non-neutral plasmas can support the gyrokinetic ITG, ETG, PTG, antiproton temperature-gradient and universal instabilities even in slab geometry. However, we found that in most cases the physics of these instabilities was different in non-neutral plasmas. We note here some of the major differences between these gyrokinetic instabilities in quasineutral and non-neutral plasmas as well as a summary of some qualitative differences which is shown in table 1.
Table 1. Qualitative differences and similarities between the different types of gyrokinetic modes arising in both quasineutral and non-neutral plasmas.

Quasilinear cross-field particle flux was investigated for each instability and it was found that the quasilinear particle flux was intrinsically ambipolar as it is in standard quasineutral gyrokinetics. We were also able to verify this numerically in each case and plot a scaled version of the particle current up to an unknown positive constant.
We found many differences between the unstable modes arising in quasineutral and non-neutral plasmas. Similarly to quasineutral plasmas, we found that non-neutral electron–ion plasmas can support the universal instability driven by a density gradient. However, in non-neutral plasmas the universal instability has a second stability threshold for large density gradients that does not exist in the quasineutral case. We found that non-neutral plasmas can also support electron and positron temperature-gradient-driven instabilities. Contrary to the case for quasineutral plasmas, we found that non-neutral pair plasmas can support both ETG and PTG modes even when each species has the same temperature and without the need for ion contamination. We also found that the ETG instability can exist even in pure electron plasmas and it can hence be reasoned that the PTG instability should also exist in a pure positron plasma. It was found that similarly to their quasineutral counterparts, the Debye length has a stabilising effect on temperature-gradient-driven instabilities. It was found that the quasilinear particle fluxes were ambipolar in each instance.
It is worth remarking that instabilities which exist even in quasineutral plasmas e.g. ETG in pure pair plasma with different species temperatures (
![]() $T_{e}\neq T_{i}$
) might somehow be of more importance in the non-neutral setting. In a quasineutral plasma, different electron and positron temperature profiles are unlikely in steady state, since the characteristic time of energy exchange between species is comparable to the Maxwellisation time. However, in non-neutral plasmas, such scenarios become much more physically realisable. So it might be more likely that this instability manifests experimentally in non-neutral plasmas. These results may have particular interest in the upcoming PAX/APEX experiments to investigate the stability of electron–positron plasmas. Indeed, in the aforementioned experiments it will be necessary to confine pure electron and pure positron plasmas and hence the stability of such systems is of great importance.
$T_{e}\neq T_{i}$
) might somehow be of more importance in the non-neutral setting. In a quasineutral plasma, different electron and positron temperature profiles are unlikely in steady state, since the characteristic time of energy exchange between species is comparable to the Maxwellisation time. However, in non-neutral plasmas, such scenarios become much more physically realisable. So it might be more likely that this instability manifests experimentally in non-neutral plasmas. These results may have particular interest in the upcoming PAX/APEX experiments to investigate the stability of electron–positron plasmas. Indeed, in the aforementioned experiments it will be necessary to confine pure electron and pure positron plasmas and hence the stability of such systems is of great importance.
The ITG mode also exists in non-neutral electron–ion plasmas. However, the growth rate is no longer simply monotonic. We also found a change in the flux direction of both particle species for sufficiently large ion fraction. We also found that temperature-gradient-driven modes exist even when the heavy species and light species carry the same sign of charge. We found unstable antiproton temperature-gradient-driven modes in electron–antiproton plasmas.
We were able to use our model to investigate drift-wave instabilities in fully un-neutralised multi-species plasmas, that is, plasmas in which all species have the same type of charge, paying particular attention to electron–antiproton plasmas. We were able to make contact with some existing work on this subject such as the results of Dubin (Reference Dubin2010) who found similar results using a fluid model with a more realistic geometry.
We once again remark on some of simplifications invoked in this work. Particularly our use of a local theory including ambient electric field, always present in non-neutral plasma, but neglecting the shear of this field assuming the shear length exceeds the characteristic length of the modes discussed here. Furthermore, the slab geometry also neglects the centrifugal effect of the
![]() $\boldsymbol{E}\times \boldsymbol{B}$
plasma rotation in our stability calculations. It is pertinent to comment that experimentally these effects can and do have a destabilising influence in addition to the destabilising density- and temperature-gradient effects considered here. This area also warrants further investigation using a more sophisticated model. To claim that this model captures all the non-neutral plasma dynamics would be an egregious oversight, but hopefully the results presented here do allow us some physical insight into non-neutral plasmas, in particular highlighting some of the important distinctions between the nature of such instabilities in quasineutral and non-neutral plasmas. We plan to address the more complex systems including a shearing electric field in the future.
$\boldsymbol{E}\times \boldsymbol{B}$
plasma rotation in our stability calculations. It is pertinent to comment that experimentally these effects can and do have a destabilising influence in addition to the destabilising density- and temperature-gradient effects considered here. This area also warrants further investigation using a more sophisticated model. To claim that this model captures all the non-neutral plasma dynamics would be an egregious oversight, but hopefully the results presented here do allow us some physical insight into non-neutral plasmas, in particular highlighting some of the important distinctions between the nature of such instabilities in quasineutral and non-neutral plasmas. We plan to address the more complex systems including a shearing electric field in the future.
Acknowledgements
We thank P. Helander for many insightful discussions. We acknowledge T. Sunn Pedersen and the PAX/APEX experiment team for their interest in our work.