Article contents
The electromotive force in multi-scale flows at high magnetic Reynolds number
Published online by Cambridge University Press: 21 September 2015
Abstract
Recent advances in dynamo theory have been made by examining the competition between small- and large-scale dynamos at high magnetic Reynolds number 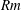 $\mathit{Rm}$. Small-scale dynamos rely on the presence of chaotic stretching whilst the generation of large-scale fields occurs in flows lacking reflectional symmetry via a systematic electromotive force (EMF). In this paper we discuss how the statistics of the EMF (at high
$\mathit{Rm}$. Small-scale dynamos rely on the presence of chaotic stretching whilst the generation of large-scale fields occurs in flows lacking reflectional symmetry via a systematic electromotive force (EMF). In this paper we discuss how the statistics of the EMF (at high 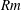 $\mathit{Rm}$) depend on the properties of the multi-scale velocity that is generating it. In particular, we determine that different scales of flow have different contributions to the statistics of the EMF, with smaller scales contributing to the mean without increasing the variance. Moreover, we determine when scales in such a flow act independently in their contribution to the EMF. We further examine the role of large-scale shear in modifying the EMF. We conjecture that the distribution of the EMF, and not simply the mean, largely determines the dominant scale of the magnetic field generated by the flow.
$\mathit{Rm}$) depend on the properties of the multi-scale velocity that is generating it. In particular, we determine that different scales of flow have different contributions to the statistics of the EMF, with smaller scales contributing to the mean without increasing the variance. Moreover, we determine when scales in such a flow act independently in their contribution to the EMF. We further examine the role of large-scale shear in modifying the EMF. We conjecture that the distribution of the EMF, and not simply the mean, largely determines the dominant scale of the magnetic field generated by the flow.
- Type
- Research Article
- Information
- Copyright
- © Cambridge University Press 2015
References
- 6
- Cited by


