Hostname: page-component-77c89778f8-9q27g Total loading time: 0 Render date: 2024-07-18T23:46:17.658Z Has data issue: false hasContentIssue false
  • English
  • Français

Effect of relativistic self-focusing on plasma wave excitation by a hollow Gaussian beam

Published online by Cambridge University Press:  01 June 2011

RUCHIKA GUPTA ,
M. RAFAT  and
R. P. SHARMA
RUCHIKA GUPTA
Affiliation:
Department of Applied Sciences and Humanities, Jamia Millia Islamia, New Delhi 110025, India (ruchikaji81@gmail.com)
M. RAFAT
Affiliation:
Department of Applied Sciences and Humanities, Jamia Millia Islamia, New Delhi 110025, India (ruchikaji81@gmail.com)
R. P. SHARMA
Affiliation:
Centre for Energy Studies, Indian Institute of Technology, New Delhi 110016, India
Get access Rights & Permissions [Opens in a new window]

Abstract

A paraxial-like approach has been invoked to understand the nature of propagation of a hollow Gaussian beam (HGB) propagating in plasma under the influence of relativistic non-linearity. In this approach, the parameters are expanded in terms of the radial distance from the maximum of irradiance rather than that from the axis. This paper investigates the excitation of plasma wave in a hot collision less plasma by HGB. On account of the 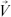× 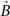force, a plasma wave at 2ω0 (here, ω0 is the pump laser frequency) is generated. The solution of the HGB has been obtained within the paraxial ray approximation. Filamentary structures of the laser beam are observed due to relativistic non-linearity.

Type
Papers
Information
Journal of Plasma Physics , Volume 77 , Issue 6 , December 2011 , pp. 777 - 784
Copyright
Copyright © Cambridge University Press 2011

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Sprangle, P. and Esarey, E. 1991 Stimulated back scattered harmonic generation from intense laser interaction with beams and plasmas. Phys. Rev. Lett. 67, 2021–2024.Google Scholar
[2]Hora, H. 1991 Plasmas at High Temperature and Density. Heildelberg: Springer.Google Scholar
[3]Kruer, W. L. 1988 The Physics of Laser Plasma Interaction, New York: Addison-Wesley.Google Scholar
[4]Sodha, M. S., Tripathi, V. K. and Ghatak, A. K. 1976 Self focusing of laser beams in plasmas and semiconductors. Prog. Opt. 13, 169–265.Google Scholar
[5]Yin, J., Noh, H., Lee, K., Kim, K., Wang, Y. and Jhe, W. 1997 Generation of a dark hollow beam by a small hollow fiber. Opt. Commun. 138, 287–292.Google Scholar
[6]Sodha, M. S., Nayyar, V. P. and Tripathi, V. K. 1974 Asymmetric focusing of the laser beam in TEM 01 doughnut mode in a nonlinear dielectric. J. Opt. Soc. Am. 64, 941–943.Google Scholar
[7]Patil, S. D., Takale, M. V., Navare, S. T. and Dongare, M. B. 2010 Focusing of Hermite-Cosh-Gaussian laser beams in collisionless magnetoplasma. Laser Part. Beams 28, 343–349.Google Scholar
[8]Heckenberg, N. R., McDuff, R., Smith, C. P. and White, A. G. 1992 Nonlinear rotation of three-dimensional dark spatial solitons in a Gaussian laser beam. Opt. Lett. 17, 221.CrossRefGoogle Scholar
[9]Gupta, M. K., Sharma, R. P. and Mahmoud, S. T. 2007 Generation of plasma wave and third harmonic generation at ultra relativistic laser power. Laser Part. Beams 25, 211–218.CrossRefGoogle Scholar
[10]Shukla, P. K., Rao, N. N., Yu, M. Y. and Tsintsadze, N. L. 1986 Relativistic nonlinear effects in plasmas. Phys. Rep. 138, 1–149.CrossRefGoogle Scholar
[11]Feit, M. D. and Fleck, J. A. Jr, 1988 Beam nonparaxiality, filament formation and beam breakup in the self focusing of optical beams. Opt. Soc. Am. B 5, 633–640.CrossRefGoogle Scholar
[12]Johnston, T. W., Vidal, F. and Frechette, D. 1997 Laser plasma filamentation and spatially periodic nonlinear Schrödinger equation approximation. Phys. Plasmas 4, 1582–1588.CrossRefGoogle Scholar
[13]Vidal, F. and Johnston, T. W. 1996 Electromagnetic beam breakup: multi filaments, single beam equilibria and radiation. Phys. Rev. Lett. 77, 1282–1285.Google Scholar
[14]Sodha, M. S., Misra, S. K. and Misra, S. 2009 Focusing of dark hollow Gaussian electromagnetic beams in a plasma. Laser Part. Beams 27, 57–68.Google Scholar
[15]Gupta, R., Sharma, P., Chauhan, P. K., Rafat, M. and Sharma, R. P. 2009 Effect of ultra relativistic laser beam filamentation on third harmonic spectrum. Phys. Plasma 16, 043101.Google Scholar
[16]Akhmanov, S. A., Sukhorukov, A. P. and Khokhlov, R. V. 1968 Self focusing and diffraction of light in a non linear medium. Sov. Phys. Usp. 10, 609–636.CrossRefGoogle Scholar